
Презентация "Окружность"

Краткое описание документа:
В данном уроке мы познакомимся с определением окружности, проанализируем характерные ей свойства, а также научимся строить и применять необходимые особенности для решения задач.
Если вы скажете, что окружностью являются все точки на одной плоскости, равноудалённые от одной точки или центра, то ответ будет неправильным, потому что в таком случае подойдёт даже квадрат. Обязательно делайте акцент на фразе «множество всех точек». Впрочем, определение и дефиниция понятны сразу, потому что многие из нас уже строили окружность с помощью циркуля.

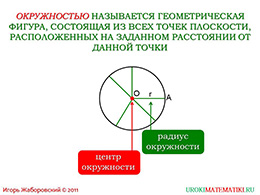
слайды 1-2 (Тема презентации "Окружность", определение окружности)
Что же означает «равно удалённость множества всех точек»? Это означает то, что если точка лежит на окружности (например, точка «А»), то отрезок «АО» является радиусом окружности и имеет одинаковое значение, не зависимо от расположения точки. Можем взять абсолютно любую другую точку, и мы будем уверенны, что это расстояние равняется отрезку «АО» и также является радиусом.
Теперь обсудим расположение окружности относительно прямой. Прямая может не пересекать окружность, иметь одну точку с окружностью или же две различные точки пересечения.
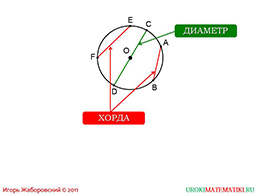
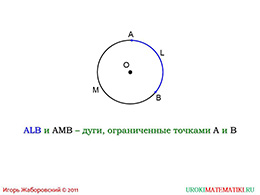
слайды 3-4 (примеры)
Если соединим две точки окружности и соединим, то получим отрезок, который носит название «хорда». На нашем примере мы видим хорды «FE» и «AB». Если хорда касается центра окружности, то она называется диаметром (у нас «CD» диаметр). Важно понимать взаимосвязь радиуса и диаметра: длина диаметра в два раза больше длины радиуса. Как думаете, какая хорда самая длинная в окружности? Если учащиеся не догадаются, то обратите внимание на диаметр и проанализируйте ответ на вопрос.
Как многие геометрические фигуры, хорда обладает рядом особенностей. Например, если в окружности есть две одинаковые хорды, то это означает, что они находятся на одинаковом расстоянии от центра окружности. Во-вторых, при проведении перпендикуляра к хорде, он будет её делить на две равные части (истинно и обратное утверждение).
Две точки разделяют окружность на две не всегда равные части. Любая из них имеет название «дуга». Дугой называют одно из подмножеств окружности, которые образуются при разбивке принадлежащими окружности двумя точками. Любые две точки, которые принадлежат окружности, делят окружность на две части, которые и являются дугами окружности. Если разбивающие окружность точки лежат на концах диаметра, то тогда окружность делится пополам. В таком случае образовавшиеся дуги называют полуокружностями. Полуокружности делят окружность на две равные части, а дуги окружности также равны. Дуги измеряются в угловых единицах.
Однако, стоит помнить, что если две дуги равны по угловой величине, то они не обязательно равны по длине. Дуги эквивалентны только при соблюдении двух условий – одинаковой угловой величине и равных радиусах окружности.
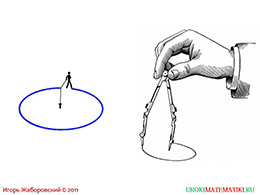

слайды 5-6 (примеры)
Один из способов построить окружность – использовать для этого специальный инструмент. Таким инструментом является циркуль. Циркуль позволяет описать окружность произвольного диаметра. Также, можно построить окружность с заданным диаметром или радиусом, а также с заданным центром. Диаметр окружности, описанной циркулем, ограничивается только размером самого циркуля. В повседневной жизни размера циркуля может не хватить для достижения поставленной цели – циркуль должен быть просто гигантским, чтобы описать окружность с диаметром, например, 20 метров. Одним из вариантов решения такой задачи может быть использование какого-нибудь колышка и верёвки. Колышек следует установить в центр предполагаемой окружности, привязать к нему верёвку, натянуть её и построить окружность от начальной точки, которая будет и конечной точкой.
Круг – это геометрическое множество точек, расстояние от которых до центра круга не превышает положительной длины отрезка радиуса. Как и в случае с окружностью, круг, радиус которого равен нулю, называется вырожденным. Границей круга является окружность по определению. Круг обладает некоторыми свойствами, характерными и для окружности – радиус, диаметр, центр. Однако, круг имеет и отличные от окружности характеристики.
Например, круг имеет площадь – произведение числа π на квадрат радиуса круга. Также, можно выделить сектор круга – часть круга, ограниченная двумя радиусами и дугой, при этом радиусы должны соединяться с концами дуги. Сектор круга – это часть круга, границей которого является дуга и стягивающая её хорда. Можно также измерить длину окружности круга, то есть его периметр, умножив радиус круга на удвоенное π. Следует отметить, что круг является выпуклой фигурой. Как и в случае с окружностью, существует особый подвид круга – единичный круг. Единичный имеет радиус, который равен единице.
Мы определили, что такое окружность и рассмотрели наиболее важные её части.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 4065 |
| Номер материала | 246 |