
Презентация "Свойства функции y=kx^2 при k меньше 0"

Краткое описание документа:
Презентация «Свойства функции y=kx^2 при k меньше 0» - мультимедийное пособие для урока алгебры 8 класса по теме «Функция y=kx^2, ее график и свойства». Она охватывает этап объяснения материала о свойствах функции y=kx^2 при отрицательных значениях числового коэффициента, а также закрепление всей изученной темы, в ходе рассмотрения которой строились графики и анализировалось их поведение, а также свойства функции при положительных значениях k. Закрепление материала производится не только на начальном уровне, но и с решением заданий более высоких уровней.
Строение презентации направлено на постепенное углубление знаний по теме. Начинается она с общей формулировки свойств данной функции, а затем разбираются примеры, при решении которых необходимо знание свойств и понимание правил поведения функции y=kx^2.


слайды 1-2 (Тема презентации "Свойства функции y=kx^2 при k меньше 0", свойства)
Объяснение материала, используя форму презентации, имеет определенное преимущество. Объяснение построено логично, цветом выделены важные части. Решение заданий сопровождается качественными рисунками. Основное преимущество – наглядность объяснения. Кроме того, на построение не тратится время урока, используется готовый материал, поэтому учитель может сконцентрировать усилия на объяснении и диалоге с учениками, контролируя формирование навыка в решении заданий, понимания изучаемых понятий.
После указания темы презентации сначала указываются свойства функции y=kx^2 при k0. Это позволяет закрепить навык определения свойств функции по известной схеме. Сначала указывается область определения функции, затем отмечается прохождение через начало координат, а затем то, что у принимает только положительные значения. В следующем пункте описывается свойство непрерывности данной функции на всей числовой прямой, наименьшее значение 0 и отсутствие наибольшего значения, участки убывания и возрастания функции.
Ученики уже овладели понятием ограничения функции, поэтому отмечается свойство ограничения функции сверху и отсутствия границы снизу. Определяется область значений функции, ее выпуклость кверху. Свойства сопровождаются рисунком, где график функции выделяется синим цветом. Четко заметно ограничение сверху, так как до контрольной прямой у=1 парабола не достает.

слайды 3-4 (свойства, пример)
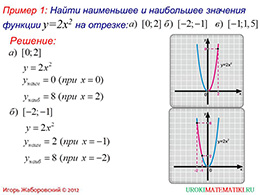
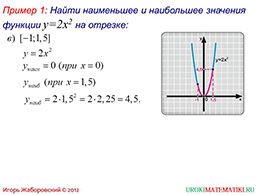
Изученные свойства функции y=kx^2, поведение графика функции, дают возможность решать задачи на исследование поведения функций при различных k. На следующем слайде ученикам представлены примеры поиска наименьшего и наибольшего значения функции y=2x^2 на разных отрезках – при возрастании функции на отрезке, при убывании, а затем возрастании на заданном отрезке, при убывании функции. Каждый участок рассматривается на отдельном рисунке.
Чтобы проанализировать поведение функции на нем, в крайних точках отмечается значение у. В зависимости от поведения функции одно из этих значений может стать наибольшим или наименьшим. Зная особенности поведения функции, ученик должен отметить на участке от -1 до 1,5 перегиб в начале координат, которое на данном участке и будет наименьшим значением функции вместо крайней точки.
слайды 5-6 (примеры)
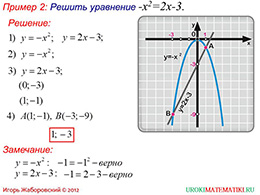
Следующий пример помогает освоить графическое представление решения некоторых уравнений. Если одна часть уравнения графически представляется прямой, а вторая – параболой, то точки пересечения данных графиков и будут решением уравнения. Две части уравнения, приравненные между собой, приравниваются у. Строится график прямой по двум точкам. Второй график – обычная парабола y=-x^2, свойства которой изучены. В пересечении двух графиков оказываются точки А(1;-1) и В(-3;-9). Соответственно значением х, корня данного уравнения, являются два значения – 1 и -3. Подставив найденные значения в обе части уравнения, убеждаемся в правильности решения.
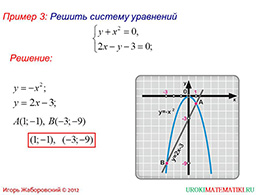
Третий пример дает представление о решении графическим способом, используя полученные знания о поведения функции, системы уравнений. Рассматривается пример, в котором первое уравнение после небольшого преобразования превращается в y=kx^2, а второе представляет собой линейную функцию. Решение примера сопровождается рисунком, на котором построены графики обеих функций и найдены их общие точки. При решении данного примера необходимо было нарисовать такие же графики, как и в предыдущем, но в данном случае ответ включает оба параметра точек, так как в систему двух уравнений входят две переменные и соответственно, их значения требуют поиска.

слайды 7-8 (примеры)
В четвертом примере полученные знания необходимо применить при исследовании сложной функции, которая состоит из простых функций на отдельных отрезках прямой х. Областью определения не является вся прямая, но на разных отрезках функция ведет себя по-разному: от -4 до 0 – это парабола с отрицательным коэффициентом, большим -1. Между 0 и 1 данная функция – прямая. Если х более 1 и менее или равно 2, она ведет себя как парабола с положительным коэффициентом.
Задание составное и содержит поиск значения функции в определенных точках, построение графика функции, перечисление свойств функции по известной схеме. Чтобы решить первую часть задания, необходимо сначала определить, к какому участку относится данное значение, а затем подставить это значение в соответствующую формулу и найти значение. При этом одна из точек не принадлежит ни одной области определения. Для решения второй части задания необходимо использовать навыки в построении графиков данных функций на разных участках, при этом важно определить правильно, какая именно часть данного графика будет частью решения.
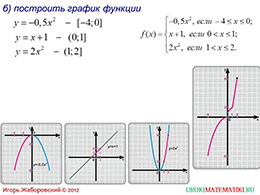
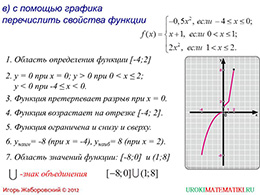
слайды 9-10 (примеры)
На последнем сайде представлены перечисленные свойства функции согласно схемы решения подобных заданий. Отмечается область определения, нули функции и знак значений, точки разрыва, участки возрастания, ограничение функции, наименьшее, наибольшее значение и область значений функции. Область значений определена объединением участков, один из которых содержит пустую точку.
Демонстрация данной презентации перед решением задач по теме «Функция y=kx^2, ее график и свойства» помогает учителю сформировать навыки учащихся в решении подобных заданий графическим способом, а также закрепить навыки исследования функции, описания ее свойств по схеме. Данная презентация может быть использована учеником для самостоятельного изучения темы, а также эффективна при подаче материала при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 6183 |
| Номер материала | 289 |