
Урок "Функция y=kx^2"

Краткое описание документа:
Продолжая курс увлекательных обучающих видеоуроков по курсу математики за 8 класс, мы рассмотрим новую для нас функцию. Предложенная функция имеет вид у = kx2, причем в данном случае следует отметить, что коэффициент k, расположенный перед аргументом х, может быть любым числом, которое отличительно от нуля.
С функцией зритель уже встречался ранее в наших видеоматериалах, только тогда она имела вид у = x2, что и рассматриваемая функция, только с коэффициентом, равным единице. График функции называется «параболой». При желании пройденный материал можно восстановить в памяти, посмотрев соответствующее видео.
Вид графика у = kx2 с коэффициентом 1, уже известно. Поэтому далее в видео будет рассматриваться поведение функции при его изменениях.
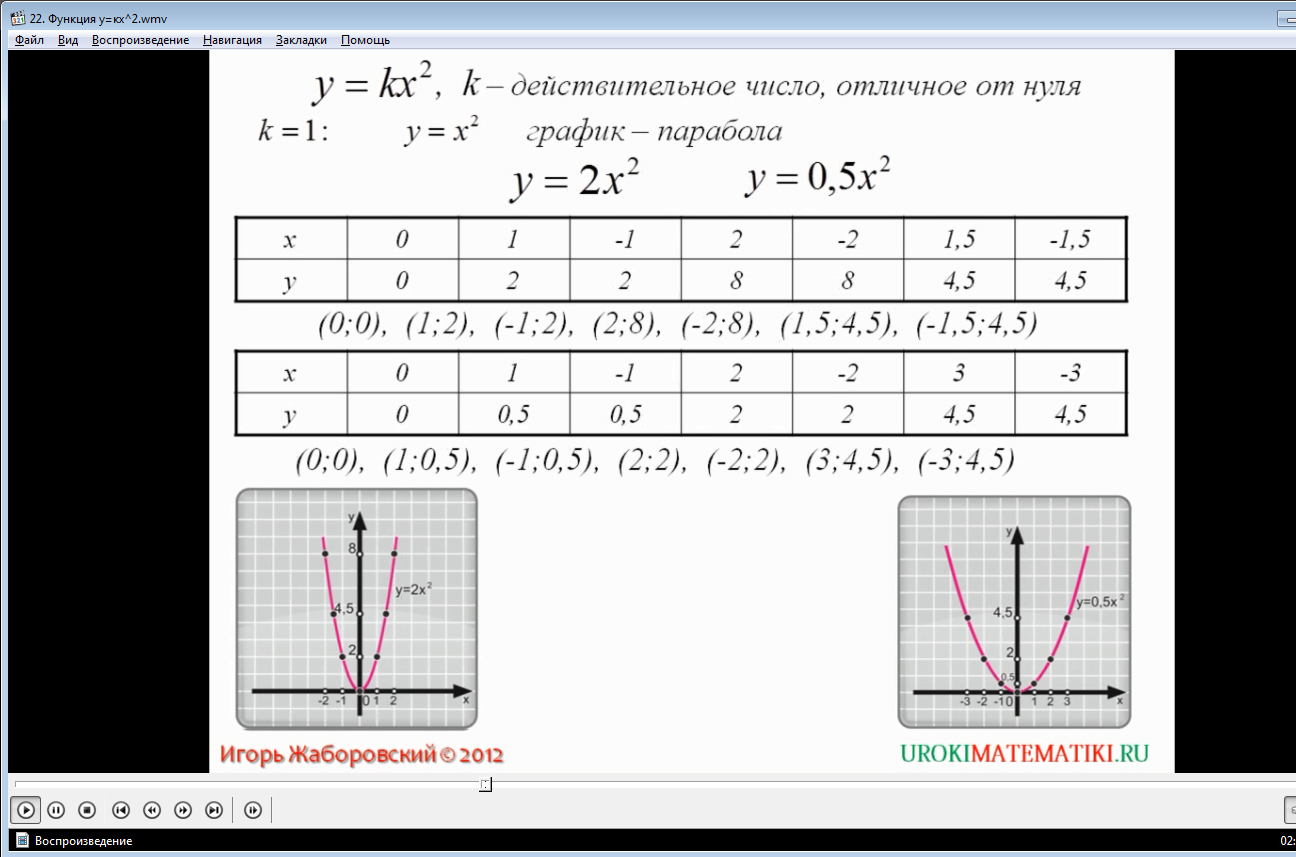
Большую наглядность демонстрируют приведенные примеры графиков для уравнений: y = 2x2 и y = 0,5x2.
Сначала рассматривается первая функция y = 2x2. Перед началом построения графика рассчитываем путем подставления значения аргумента x в заданное равенство. Само построение графика смотрите в нашем видео.
По тому же алгоритму рассчитываем и координаты построения графика функции y = 0,5x2. Построение точек, а также самого графика более детально смотрите в видео.

Если сравнить все три представленных графика y = kx2, то отчетливо видно, что они между собой похожи, все они - параболы; начала координат является их вершиной, а ось ординат - ось симметрии этого графика. Коэффициент, расположенный возле аргумента x, влияет на крутизну параболы, причем, чем он больше, тем график более крутой. В представленном видеоматериале мы можете это увидеть в системе координат, на которой эти параболы совмещены.
Так же дела обстоят и с каждой функцией заданного вида, когда коэффициент является положительным. График этой функции y = kx2 также парабола, вершина расположена в точке начала координат, ветви параболы имеют направление вверх, на крутизну графика влияет величина коэффициента, причем с увеличением его значения крутизна графика увеличивается. Ось ординат в данном графике и является осью симметрии параболы.
Для удобства использования математики придумали свои сокращения, например, вместо названия «парабола, которая служит графиком функции y = kx2», используют «парабола y = kx2», и вместо уже известного нам термина «ось симметрии параболы» говорят просто «ось параболы».
До этого мы рассматривали поведение указанной функции, если коэффициент имеет положительное значение. А как же будет вести себя функция у = kx2 в случае, если мы имеем отрицательное значение этого коэффициента? Подробно об этом смотрите в видео.
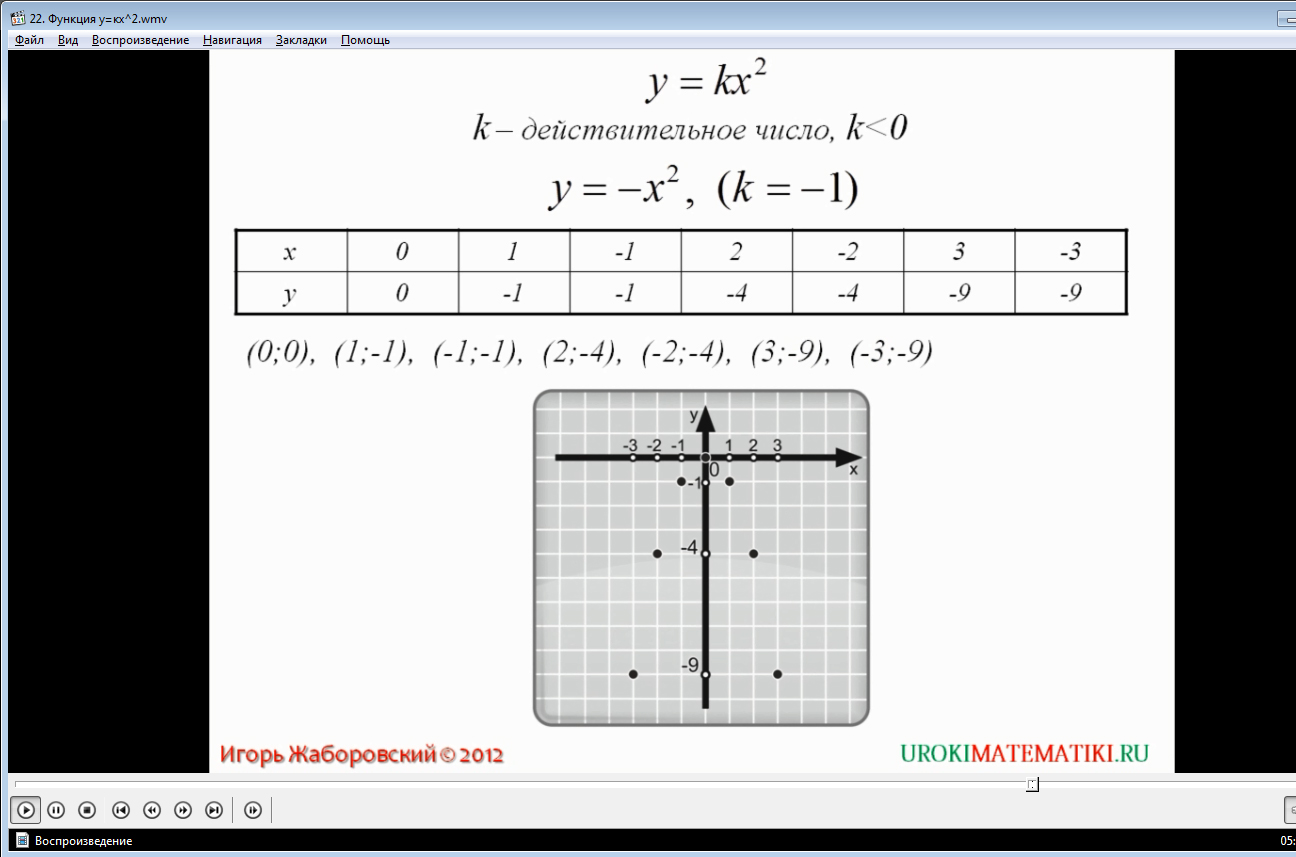
Объяснения более понятны в том случае, когда присутствует наглядность объясняемого процесса. Для этого в видео нам рекомендуется построить график функции вида: у = - х2 (здесь k = - 1). Расчеты координат проводят по алгоритму, упомянутому выше, изображение графика также представлены в видео. Следует обозначить, что графиком также является парабола с вершиной в начале оси координат, но здесь ветки параболы имеют нисходящее направление. Такие же характеристики характерны и для других графиков функций такого типа с коэффициентом со знаком минус.
В заключение следует отметить, что график равенства y = kx2, когда коэффициент не равняется нулю, является параболой с вершиной в точке начала координат; ось y является осью симметрии параболы; ветви направлены вверх при положительном значении коэффициента, и вниз - при его отрицательном значении.

Также для наглядности в видео рекомендую построить графики для уравнений y = x2, а также y = -x2. Осуществив эту операцию, нетрудно сделать вывод, что эти графики являются симметричными между собой относительно оси x. Ту же закономерность можно заметить в случае построения любых двух графиков равенства, имеющих противоположные знаки возле одинаковых коэффициентов.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7384 |
| Номер материала | 545 |