
Урок "Свойства функции y=kx^2 при k больше 0"

Краткое описание документа:
На этом уроке мы продолжим знакомство с функцией y = kx2 и рассмотрим свойства функции y = kx2 при k > 0.
Графиком этой функции является парабола, а посколькуk > 0, то ветви параболы будут направлены вверх.
Воспользуемся графиком функции y = kx2 при k > 0 или, иначе говоря, ее геометрической моделью, и разберем свойства этой функции. Смотрите видеоурок.
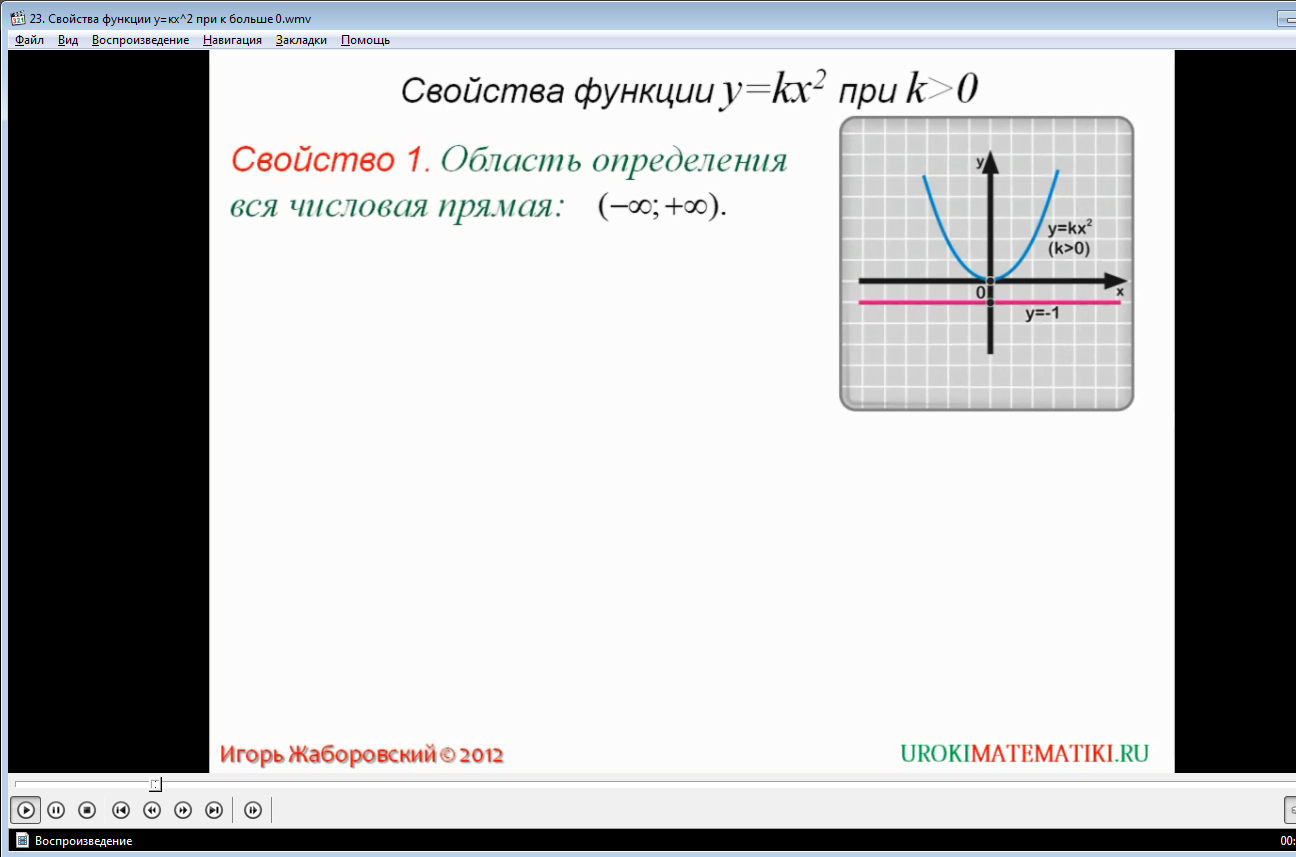
Свойство 1. Область определения функции. Как известно, область определения функции составляют все значения, которые принимает независимая переменная x(аргумент). Наша функция определена на всей числовой прямой. Действительно, для любого значения аргумента x мы можем по формуле y = kx2 определить y. Таким образом, область определения функции – вся числовая прямая: (-∞;∞)
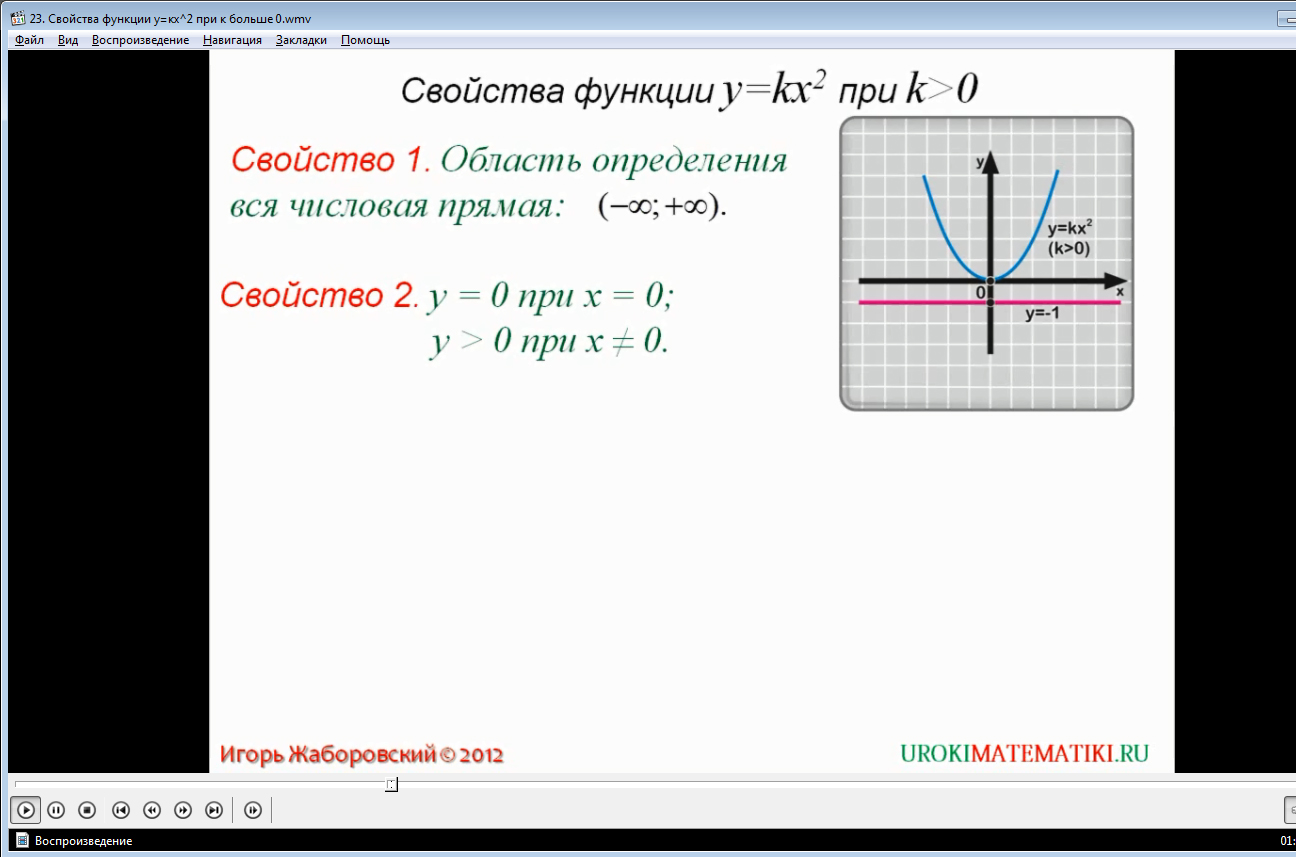
Свойство 2. y = 0 при х = 0;
y > 0 при х не равен 0.
По графику нашей функции видно, что при х = 0 функция обращается в нуль, и график ее проходит через начало координат. Мы видим, что график расположен выше оси х. Данное свойство можно объяснить еще и так. По условию k > 0 (число положительное). При x < 0 x2 также число положительное. Значит, y = kx2 как произведение положительных чисел тоже будет числом положительным. Таким образом, мы обосновали свойство 2 без помощи графика.
Свойство 3. y = kx2 - непрерывная функция. Непрерывность функции на некотором промежутке означает, что график функции на этом промежутке сплошной, не имеет разрывов. Действительно, она принимает сплошь все численные значения от 0 до∞.
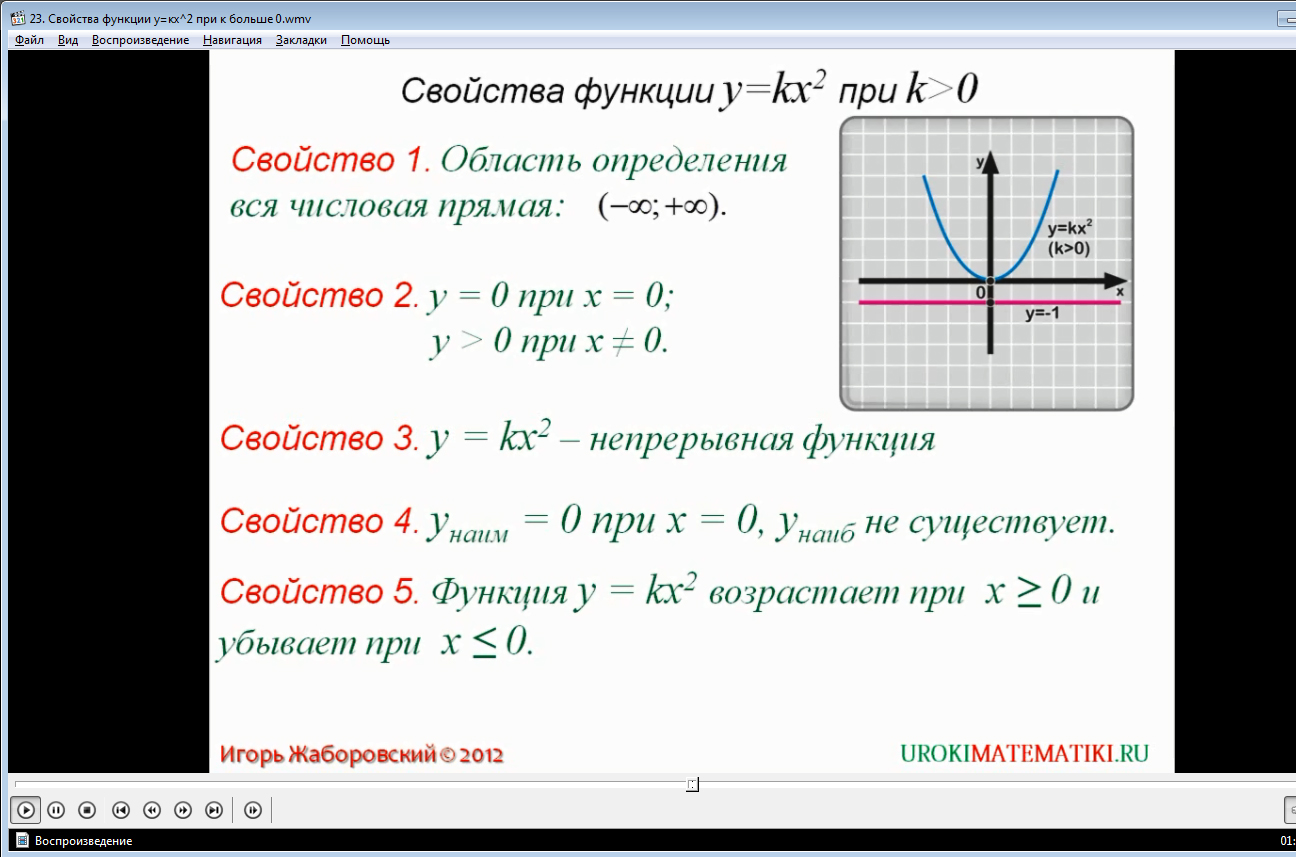
Свойство 4. Функция имеет наименьшее значение, или минимум. Это значение равно нулю, то есть унаим = 0. Это значение достигается при х = 0. Как видно по графику функции y = kx2, наибольшего значения (максимума) у нее не существует.
Свойство 5. Функция y = kx2 возрастает при x больше или равно 0 и убывает при х меньше или равен 0.
Возьмем два любых отрицательных значения аргумента, например, х1 = -2 и х2 = -4.
Тут x1 > x2. Пусть k = 2. Тогда y1 = kx2 = 2 * (-2)2 = 8; y2 = kx2 = 2 * (-4)2 = 32.
Мы видим, что y1 > y2, то есть большему значению аргумента (x1 = -2) соответствует меньшее значение функции y1 = 8. Значит, функция убывает при x меньше или равен 0. График спускается к точке х = 0.
Аналогично, если взять два любых положительных значения аргумента, например х1 = 2 и х2 = 4, то есть x1 < x2, то y1 = kx2 = 2 * (2)2 = 8; y2 = kx2 = 2 * (4)2 = 32. Получили, что y1 > y2, то есть большему значению аргумента соответствует большее значение функции. Значит, функция возрастает при x больше или равен 0 . График поднимается от точки х = 0.
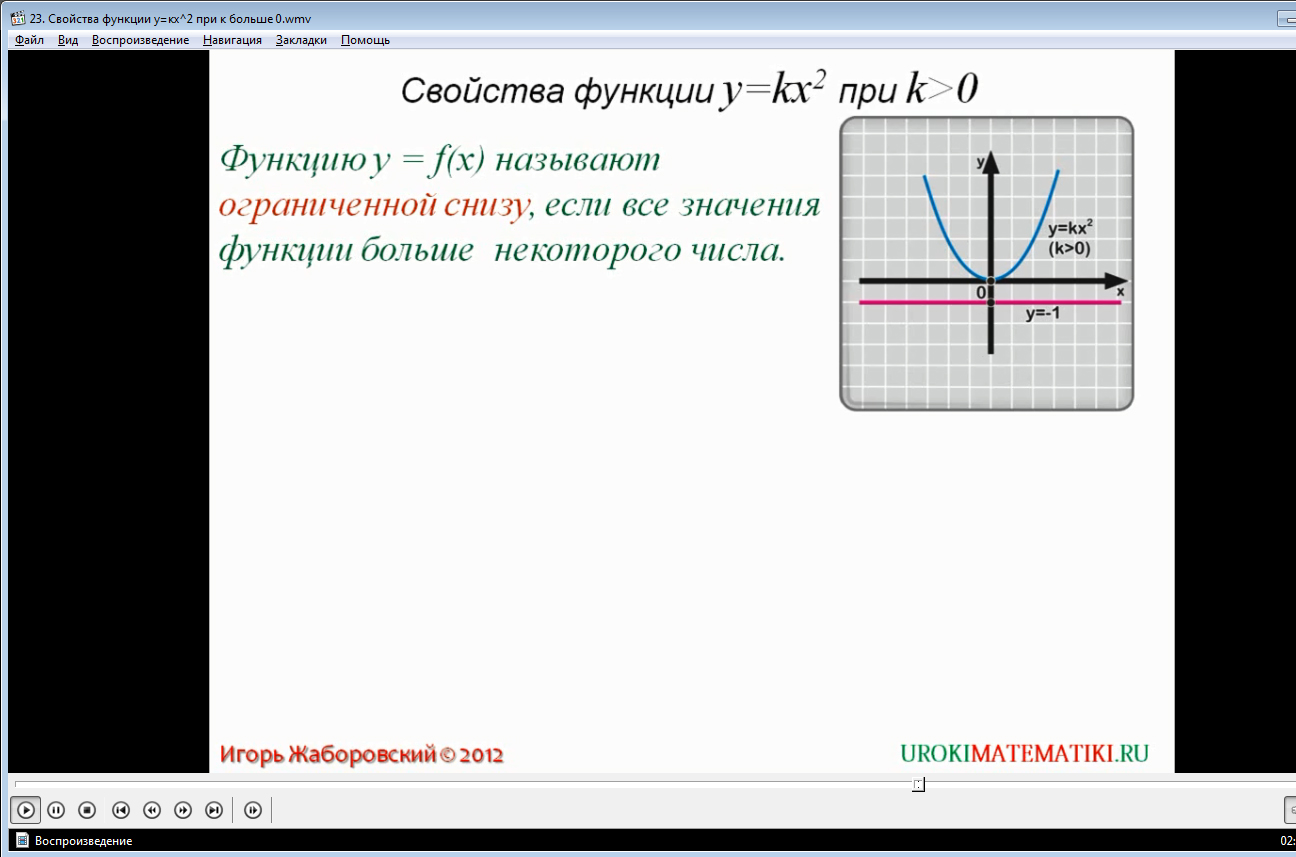
Свойство 6. Функция y = kx2 (k > 0) ограничена снизу и не ограничена сверху.
Функции, которые мы рассматриваем, могут быть ограниченными и неограниченными. Что это означает, смотрим и слушаем в видеоуроке.
Свойство 7. Область значения функции y = kx2 (k > 0) – луч [0; ∞).
Область значения функции – это все значения, которые может принимать зависимая переменная, то есть y. В нашем случае y принимает все значения от 0 до∞.
Свойство 8. Функция выпукла вниз.
Это значит, что если мы соединим две точки графика отрезком прямой, то часть графика, находящаяся между этими точками, будет лежать ниже отрезка.
Сложение и вычитание алгебраических дробей с разными знаменателями
В этом видеуроке вы познакомитесь с алгоритмом сложения (вычитания) алгебраических дробей, алгоритмом отыскания общего знаменателя для нескольких алгебраических дробей, правилом приведения алгебраических дробей к общему знаменателю. Это все пригодится для понимания и упрощения решений многочисленного количества заданий по теме.
Алгоритм:
Шаг 1. Привести дроби к общему знаменателю; в случае, когда они с самого начала имели одинаковые знаменатели, этот шаг опускается.
Шаг 2. Выполнить сложение (вычитание) полученных дробей с одинаковыми знаменателями.
Рассмотрим пример. Выполнить действия.
а) 3а/4 + 2а/5; b) 2a/3b2 + 5a2/6b3; c) a/(a + b) – a/(a – b).
Решение.
a) 3a/4 + 2a/5 = 15/20 + 8a/20 = 23a/20.
Для дробей 3a/4 и 2а/5 общий знаменатель - число 20 (оно делится на 4 и 5), выступает общим кратным и наименьшим общим кратным.
b) 2a/3b2 + 5a2/6b3 = (2ab + 5a2)/18b3.
Для дробей 2a/3b2 и 5a2/6b3 общий знаменатель одночлен 18b3 (делится на 3b2 и 6b3).
c) a/(a + b) – a/(a – b) = (a2 - ab)/(a2 – b2) – (a2 + ab)/(a2 – b2) = ((a2 – ab) – (a2 + ab))/(a2 – b2) = (a2 – ab – a2 – ab)/(a2 – b2) = -2ab/(a2 – b2).
Для дробей a/(a + b) и a/(a - b) общий знаменатель - это произведение (a + b)(a - b), так как оно делится и на a + b, и на a - b.
Далее вы можете ознакомиться с алгоритмом отыскания общего знаменателя для нескольких алгебраических дробей.
Шаг 1. Разложение всех знаменателей на множители.
Шаг 2. Поиск НОК для числовых коэффициентов, которые находятся в разложениях на множители при выполнении первого шага.
Шаг 3. Составление произведения, что содержит в качестве множителей все буквенные множители разложений, которые вы получите при выполнении первого шага алгоритма.
Шаг 4. Приписывание к произведению, которое выйдет на третьем шаге, числового коэффициента, найденного на второй позиции. В результате вы найдете общий знаменатель.
Применение алгоритма при решении примеров вы сможете увидеть в видео.
После того, как был оформлен алгоритм поиска общего знаменателя для нескольких алгебраических дробей, может возникнуть ряд вопросов к его пониманию. Для этого Вам следует ознакомиться с его упрощенной формулировкой, а именно правилом приведения алгебраических дробей к общему знаменателю, которое представлено в видеуроке.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8945 |
| Номер материала | 546 |