
Презентация "Функция y=kx^2"

Краткое описание документа:
Презентация «Функция y=kx^2» - удобное мультимедийное пособие для изучения темы «Функция y=kx^2, ее свойства и график». Это одна из наиболее важных тем, определяющих большую часть материала, изучаемого в старших классах. Функция y=kx^2 – самая простая форма квадратичной функции. Понимание принципа построения графика квадратичной функции, отличия графиков с различными коэффициентами, сходство с поведением графика линейной функции при изменении коэффициента – важная часть глубокого освоения материала, обеспечивающая понимание поведения сложных функций, изучаемых на более поздних этапах школьной алгебры.
В целом, тема средней сложности для понимания восьмиклассников. Если же ученик недостаточно внимательный на уроке, тема может быть не понята, что вызовет затруднение при решении заданий в дальнейшем и освоении методов построения и понимания свойств графика квадратичной функции. Поэтому для концентрации внимания учеников используются все доступные учителю методы, среди которых и демонстрация презентации. При помощи данной презентации учитель продолжает формировать умение учеников строить графики функций. Ученик осваивает различные методы построения. Углубляется понимание учеником функции, ее поведения, построения графика.

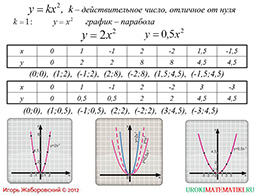
слайды 1-2 (Тема презентации "Функция y=kx^2", пример)
Презентация строится следующим образом. Сначала подробно рассматривается построение графика функции для различных коэффициентов. Наблюдение за поведением графика функции дает возможность сделать выводы о свойствах данного графика. Рассматривается поведение графика линейной функции для сравнения, после чего график функции рассматривается для отрицательного значения коэффициента. Это дает возможность сделать соответствующие обобщающие выводы о свойствах и поведении графика функции.
Такая форма подачи материала на уроке целесообразна, так как есть возможность представить графику при помощи нескольких цветов, выделяя определенные моменты, а также анимацию для лучшей демонстрации процесса построения, поведения графика.
Начинается презентация с общего представления функции y=kx^2. Затем уточняются частные случаи для различных числовых коэффициентов. Предлагается две функции – одна с коэффициентом больше 1, вторая – с дробным числом больше 0 и меньше 1. Для построения графика функции точки представлены в табличном виде. После заполнения таблицы значениями х и у определяются точки, при помощи которых строится график функции. Ниже таблиц для функций, приведенных в примере, нарисованы графики.
После построения данных функций сформирован отдельный рисунок, где нарисован график функции с k=1, а затем графики функций для данных примеров. На рисунке хорошо видно поведение графика при изменении числового коэффициента. Учитель отмечает, что при увеличении коэффициента больше 1 график функции сильнее прижимается к оси у, а при приближении коэффициента, меньшего 1, к нулю, график сильнее прижимается к оси х.

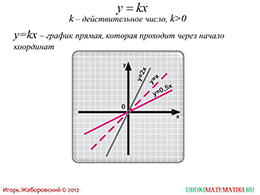
слайды 3-4 (график)
После построения данных функций сформирован отдельный рисунок, где нарисован график функции с k=1, а затем графики функций для данных примеров. На рисунке хорошо видно поведение графика при изменении числового коэффициента. Учитель отмечает, что при увеличении коэффициента больше 1 Из данных примеров можно сделать соответствующие общие выводы, отображенные на следующем слайде. Описывается поведение графика функции для коэффициента, большего нуля.
Для лучшего запоминания учащимися зеленым цветом выделен текст о том, что график данной функции – парабола с ветвями, направленными вверх и при увеличении коэффициента k график становится более крутым. К тому же график симметричный относительно оси у. Дальше на этом графике отображается словесное описание математических выражений, которые могут употребляться при описании данной функции. Под упрощенным названием «ось параболы» понимается рассмотренная ось симметрии, а парабола y=kx^2 – это график данной функции.
Следующий слайд напоминает учащимся поведение графика линейной функции с положительным числовым коэффициентом. Напоминается, что этот график – прямая. При увеличении числового коэффициента прямая становится более крутой и сильнее прижимается к оси у, а при приближении числового коэффициента к 0 график сильнее прижимается к оси х. В данной особенности графики обеих функций сходны.функции сильнее прижимается к оси у, а при приближении коэффициента, меньшего 1, к нулю, график сильнее прижимается к оси х.
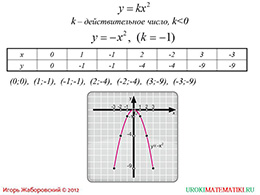

слайды 5-6 (примеры)
Следующий слайд – демонстрация поведения функции y=kx^2 при отрицательном числовом коэффициенте. Для примера берется наиболее простой случай, где коэффициент равен -1. После подстановки в функцию значения х и вычисления у, составляется табличное описание поведения функции, определяются точки для построения и ниже строится график. В результате построения отмечается особенность данного графика - ветви параболы направлены вниз. После наблюдения поведения функции при отрицательных значениях может быть сделан и общий вывод.
На следующем слайде информация, полученная в результате построения, наблюдения и обобщения, представляется в общем виде. Дается словесное описание графика функции с указанием всех его свойств – вершиной в начале координат, осью симметрии, различным направлением ветвей при коэффициентах разного знака. В конце отмечается симметричность графиков функций с коэффициентами 1 и -1 относительно оси абсцисс.
В ходе данной презентации подробно и понятно разъясняются правила поведения функции y=kx^2 для различных случаев, поэтому она может быть рекомендована и для самостоятельного изучения. Также она может использоваться в ходе объяснения при дистанционном обучении. На уроке алгебры учитель может применить данную презентацию в качестве наглядного материала в ходе объяснения новой темы.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5305 |
| Номер материала | 287 |