
Презентация "Свойства функции y=k/x, при k меньше 0"

Краткое описание документа:
Курс алгебры насыщен всякого рода функциями, которые играют важную роль. Изучение темы «Свойства функции y=k/x, при k меньше 0» позволяет решать ряд сложнейших задач, которые невозможно решить иным способом. Также задания, содержащие именно такую функцию, часто встречаются в итоговой аттестации. Поэтому изучение данной темы крайне важно.Чтобы процесс обучения был интересен, требуется много наглядности, в качестве которой может быть использована презентация.
Чтобы учителя не тратили свое время и силы на их создание, автор приготовил данную презентацию. Она наполнена достаточным объемом информации, полезной для обучающихся. Если рассматривать презентацию по порядку, то в самом ее начале представлены свойства функции, которая заявлена в теме.
слайды 1-2 (Тема презентации "Свойства функции y=k/x, при k<0", свойства)
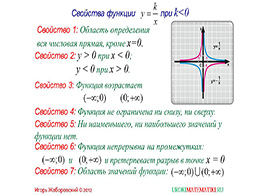
Первым свойством является область определения этой самой функции, которая включает все значения числовой прямой, кроме нуля. Далее указывается, что функция принимает положительные значения при отрицательных значениях переменной, и наоборот, отрицательные значения – при положительных значениях переменной. Также в свойствах говорится о том, что функция возрастает на всей области определения и не ограничена ни сверху, ни снизу.
Кроме того, из свойств становится известно, что у данной функции нет ни наибольшего, ни наименьшего значения. Также здесь говорится, что функция непрерывна на всей области определения, и в точке x=0 имеется разрыв. И в завершении слайда со свойствами в презентации указаны все возможные значения, которые может принимать функция. А это вся числовая прямая, но без нуля. Кроме того, автор продемонстрировал данные свойства на чертеже, который иллюстрирует график данной функции.
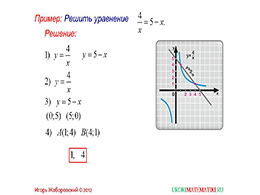
Далее автор предлагает рассмотреть примеры, где применяется данная функция и ее свойства. И первый такой пример предлагает решить уравнение, которое состоит из равенства двух функций, одна из которых представляет собой y=k/x, а другая линейная. Чтобы решить данное уравнение, следует заметить, что значения функций будут равны, если переменные их будут иметь равные значения, а значит, графики этих функций будут пересекаться в точках. Соответственно, решениями данного уравнения будут абсциссы точек пересечения данных графиков.

слайды 3-4 (примеры)
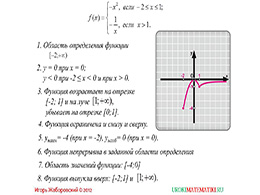
Другими словами, в данном примере требуется построить графики функций, которые записаны по разные стороны от знака равенства. И затем найти точки пересечения этих графиков. И теперь уже не сложно найти абсциссы этих точек. Но этот пример является одним из самых простых. В математике существует огромное множество задач, которые имеют более сложную ситуацию. И следующий такой пример является тому подтверждением.Второй пример показывает, как построить график сложной функции, где содержится как элемент заявленная в теме часть функции, и прочитать построенный график.
Прочитать график означает описать свойства функции. Чтобы построить график сложной функции, которая дается в примере данной презентации, требуется построить график каждой из предложенных функций и выделить другим цветом или линией пожирнее тот участок, который задается в написании сложной функции. Так можно построить график сложной функции. Но в задании еще требуется этот график прочитать, поэтому автор продолжает выполнение данного примера.На следующем слайде идет описания свойств только что построенной функции. И первым свойством является область определения, которая определяется уже не по формулам, по виду самой функции, а то полученному графику.

слайды 5-6 (примеры)
Затем определяется знак функции в зависимости от значения переменной, где и определилось, что функция обращается в нуль при нулевом значении переменной. По графику также видно, что функция возрастает на отрезке от минус двух до одного и на луче от одного до плюс бесконечности, убывает на отрезке от нуля до одного. Также здесь видно ,что функция ограничена снизу и сверху. И при этом имеет максимальное значение и минимальное, которые соответственно равны 0, при x=0, и -4, при x=-2. Но функция на всей своей области определения является непрерывной. Область значений функции является также ограниченной, и она заключается в отрезке от -4 до 0.
При этом функция имеет два участка выпуклости. Таким образом, все свойства данной, построенной функции описаны, а значит, график прочитан.Но на этом автор не остановился. Он в данной презентации показывает еще и третий пример, который можно отнести к разряду сложных. Но сложность заключается в самом только лишь задании. Тут-то автор и показывает, как легко можно доказать равенство, которое дается в задании. Здесь просто нужно вместо переменной x вставить в функцию то выражение, которое дается в скобках. Осуществляя математические преобразования, равенство легко доказывается.Данную презентацию учитель может смело использовать на уроке при изучении темы «Свойства функции y=k/x, при k<0». В этом случае не придется тратить много времени на подготовку к уроку, ведь все важное и необходимое автор здесь учел.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4339 |
| Номер материала | 292 |