
Презентация "Касательная к окружности"

Краткое описание документа:
Школьникам восьмого класса предстоит ознакомиться с таким понятием, как касательная. В дальнейшем она будет фигурировать в различных задачах, теоремах и доказательствах. При изучении производной в старших классах школьники также столкнутся с понятием касательная. Благодаря данному электронному обучающему пособию, можно ознакомиться с тем, что такое касательная к окружности, как ее необходимо изобразить и какими свойствами она обладает.
Презентация содержит в себе три информативных слайда. Желательно, чтобы объяснения сопровождались параллельно с показом мультимедийного обучающего файла. Таким образом, учащиеся лучше поймут материал и запомнят содержимое.
Итак, рассмотрим первый слайд. Здесь можно увидеть геометрическое изображение окружности. Центр окружности обозначен традиционно буквой О. Также, можно увидеть прямую, которая пересекается с окружностью в одной точке. Каким образом могут быть взаимно располагаться прямая и окружность было рассмотрено в предыдущем уроке. Прямая может пересечь окружность в двух точках, в одной точке или вовсе не пересекаться с ней.

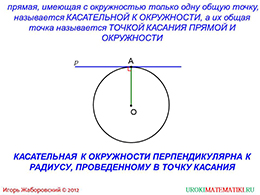
слайды 1-2 (Тема презентации "Касательная к окружности", определение касательной к окружности)
В случае касательной, прямая должна пересекаться с окружностью в одной точке. Определение дается над иллюстрацией. Прямая, как и в прошлом уроке, обозначена через латинскую букву p. Из предыдущего урока необходимо вспомнить то, что в случае одной общей точки между прямой и окружностью, расстояние от центра окружности до прямой является равным радиусу, иными словами, и является радиусом. По термином расстояние подразумевается высота, опущенная от центра окружности О до прямой p. Угол, который образуется между высотой OA и данной прямой, является прямым. Таким образом, любая касательная к произвольной окружности будет составлять прямой угол с радиусом.
Прейдем к следующему слайду. Здесь рассматривается обратный случай. Если провести прямую через конец радиуса таким образом, чтобы она составила прямой угол с ним, то такая прямая будет являться касательной для окружности, которой принадлежал радиус.
На данной странице предлагается рассмотреть следующий случай. Для начала проводятся дополнительные построения. Проведем два радиуса: OC и OB. Пусть некоторая точка A не принадлежит окружности, то есть лежит вне окружности. Соединим отрезками точки А и O, A и B, A и C. Отрезки AO, AB, как видно из рисунка, лежат на касательных окружности. Согласно свойству, которое рассматривается на данной странице, эти отрезки равны.
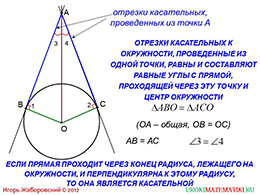
слайды 3-4 (примеры)
Также, углы, которые находятся между отрезками, лежащими на касательных и разделяющим отрезком, который проходит через центр окружности, являются равными. Данное выражение стоит запомнить, оно пригодится при решении практических геометрических задач.
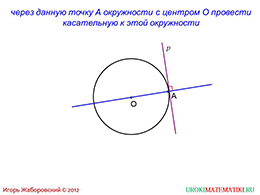
Для закрепления материала, автор предлагает провести касательную через точку А, которой лежит на некоторой с центром в точке О. На презентации анимационно показывается процесс построения. Он не включает в себе ничего сложного. Как видим, для начала, проводится прямая через центр окружности и точку А. Как известно из основных геометрических аксиом, через две точки можно провести одну и только одну прямую. На последнем этапе необходимо провести через точку А некоторую прямую, таким образом, чтобы являлась перпендикуляром для первой прямой.
На этот материал в презентации заканчивается. Чтобы продолжить изучение, необходимо перейти к следующему файлу. Благодаря данным обучающим урокам, школьная геометрия станет более понятной, простой и доступной.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5705 |
| Номер материала | 349 |