
Урок "О подобии произвольных фигур"

Краткое описание документа:
В этом виде уроке мы подробно рассмотрим такое важнейшее геометрическое определение, как подобие фигур. Подобие, не смотря на кажущуюся простоту, является довольно сложным и многогранным термином, который можно выразить в нескольких разделах геометрии. В видео, конечно же, будет ориентирование на планиметрию и эвклидово плоское пространство, без экзотических и сложных формул.
Чаще всего подобие определяется двумя вариациями:
Само подобие – это произвольное преобразование некой фигуры в эвклидовом пространстве так, чтобы для выходной фигуры соблюдалось следующее равенство:
А1В1 = К*АВ
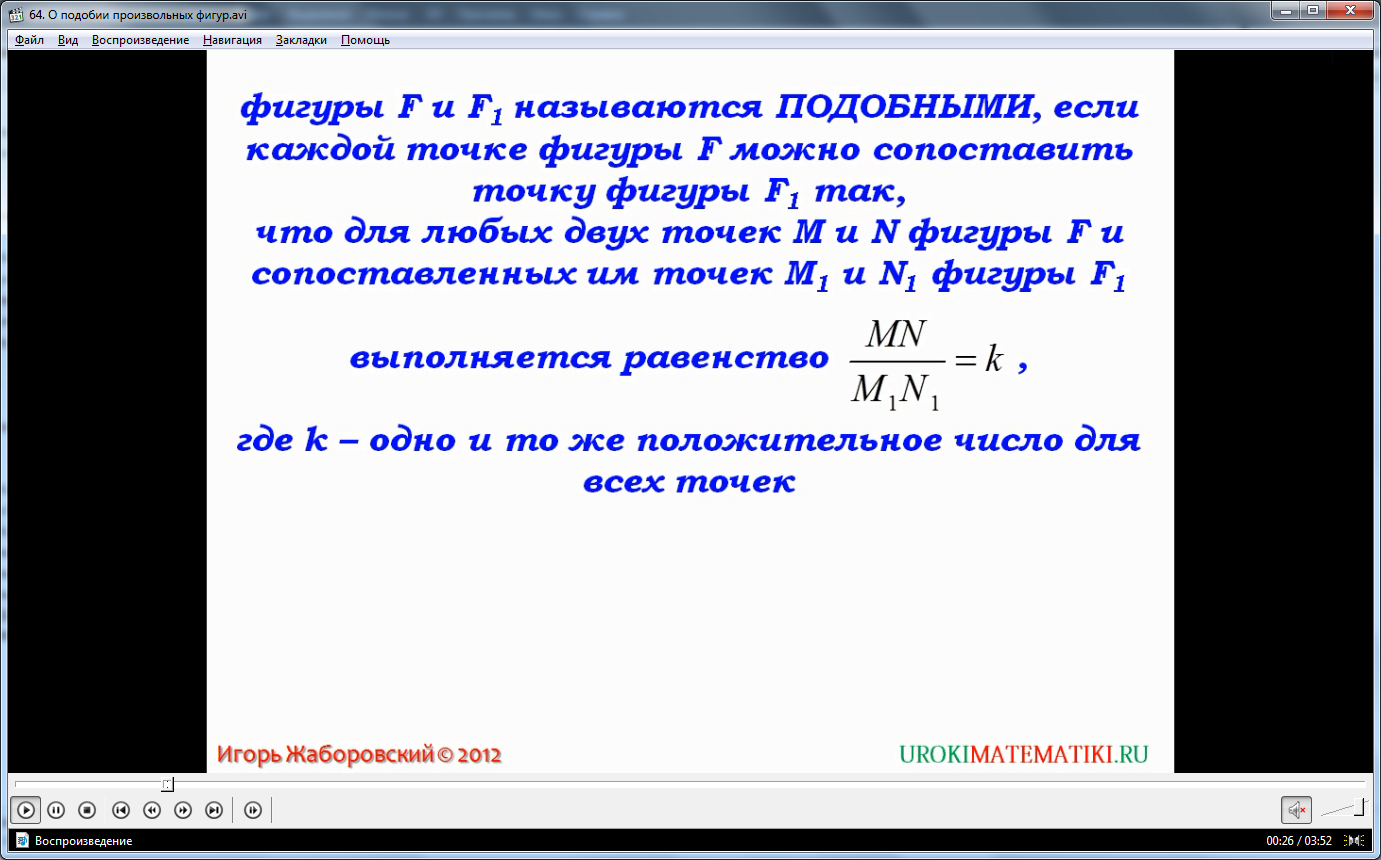
Где А и В – элементы (точки, углы и т.д.) начальной фигуры F, а А1 и В1 – элементы итоговой фигуры F1. При этом, К – коэффициент подобия фигур F и F1. Это понятие достаточно общее, чаще используют какой-либо частный случай – например, движение в эвклидовом пространстве, включая тождественную разновидность, порождает множество подобных фигур с коэффициентом подобия, равным единице. Иначе говоря, если коэффициент подобия двух и более фигур равен единице, то фигуры идентичны и равны между собой.
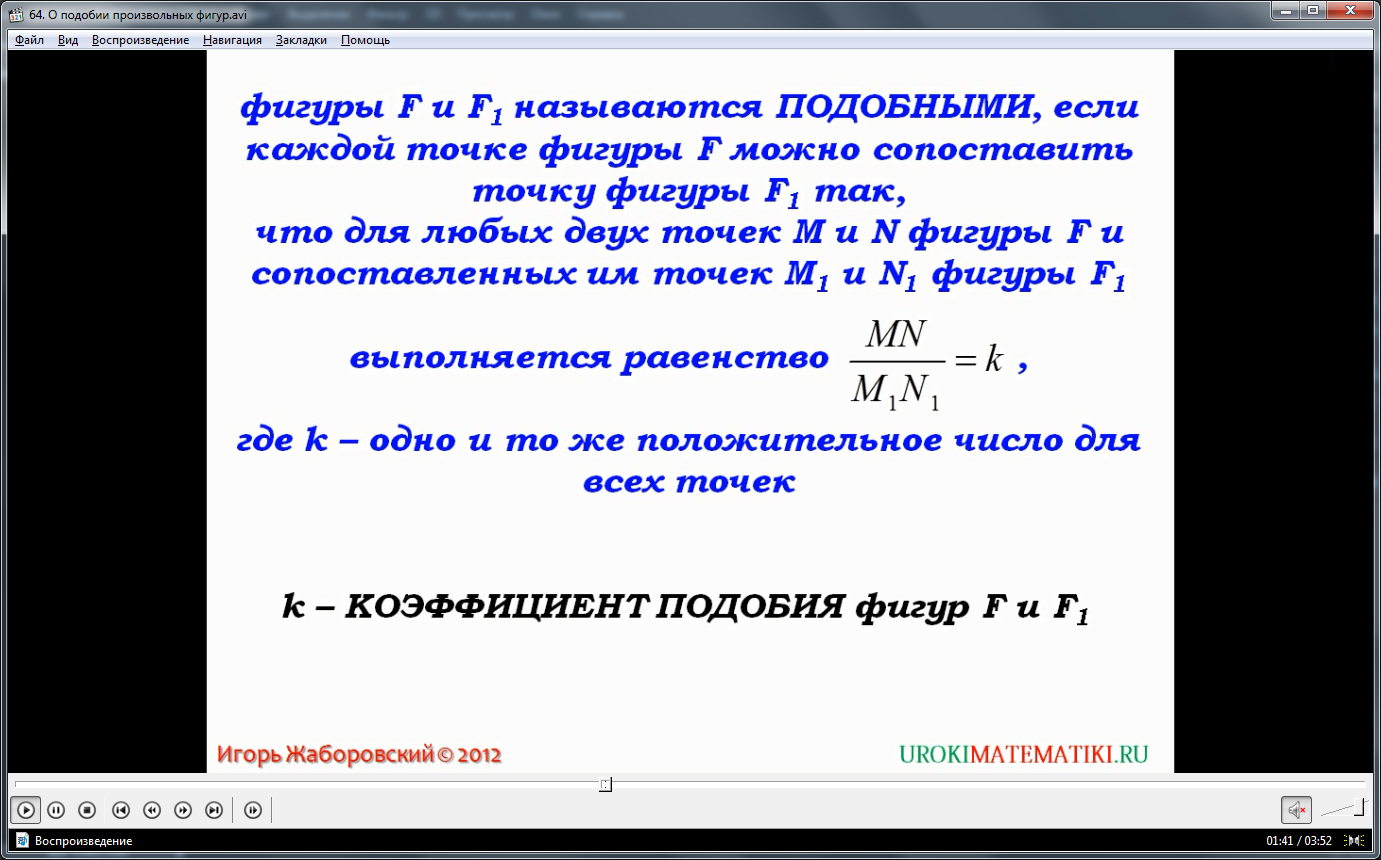
Соответственно, подобными фигурами, с коэффициентом подобия К, называют фигуры F и F1, при условии, что любые два элемента фигуры F – А и В, относятся к элементам А1 и В1 фигуры F1 через единый коэффициент К. И снова, определение достаточно общее, тут главное понять суть – любые элементы подобных фигур соотносятся через общий и постоянный коэффициент. Он может быть равен любому положительному конечному числу, быть одинаковым для любого множества выбранных фигур, если они подобны.
Собственно говоря, на практике гораздо чаще используют многочисленные частные случаи подобия. В зависимости от фигур, их свойств и особенностей, вытекает множество дополнительных правил подобия. Поэтому в задачах с подобными фигурами следует пользоваться частными правилами, опирающимися на общий закон подобия.
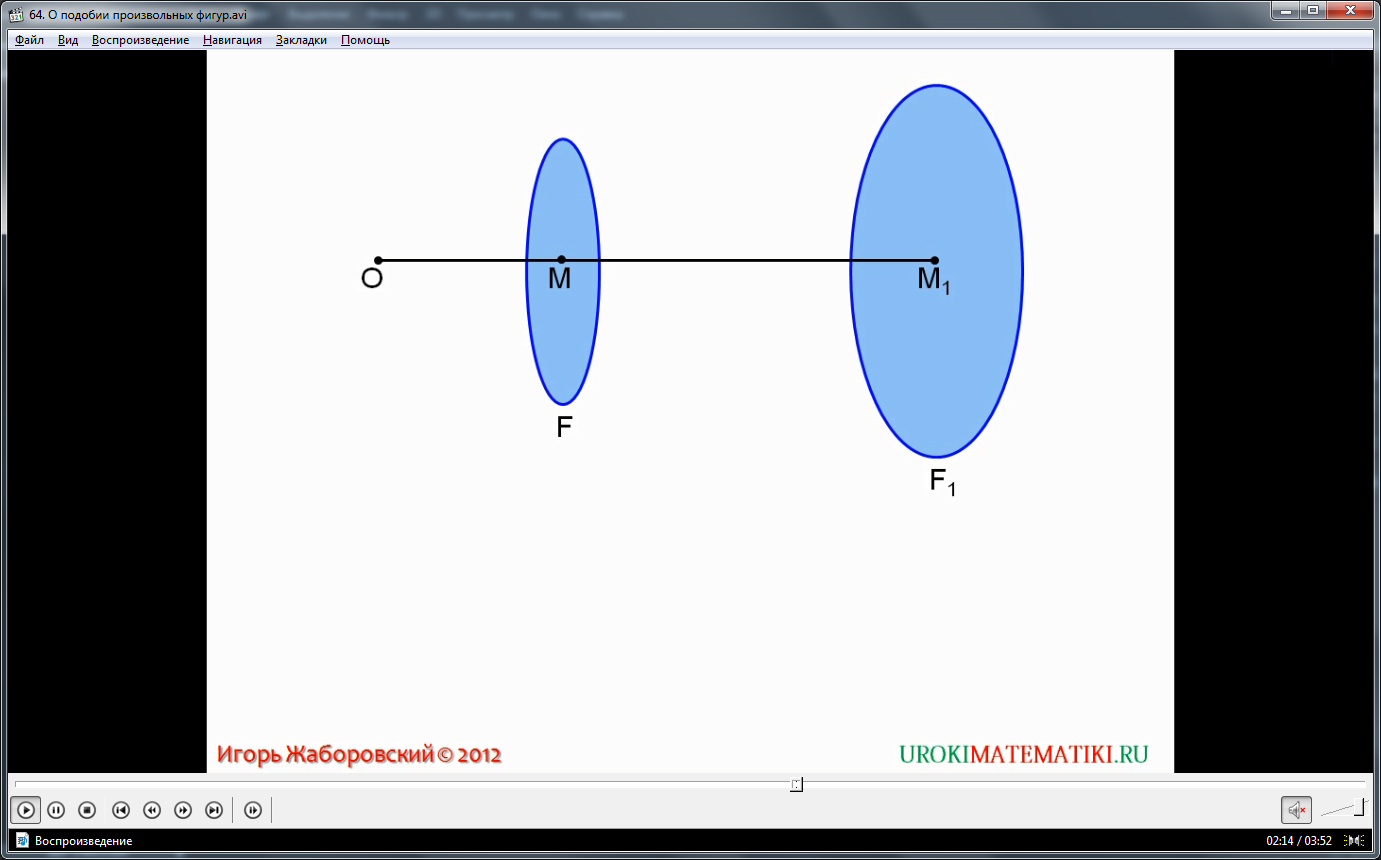
Также важно понять коренное отличие между равенством фигур и их подобием. По сути говоря, равенство – это подобие фигур с коэффициентом подобия, равном единице, частный случай подобия, параллельный перенос фигуры в эвклидовом пространстве. При этом, некоторые элементы, например, углы в треугольниках, у подобных фигур могут быть равны, а некоторые – нет, что вносит определенную путаницу в решениях. Равные фигуры всегда идентичны полностью, и всех их параметры равны между собой.

На видео есть возможность рассмотреть некоторые частные случаи подобия фигур. Например, все окружности подобны друг с другом, коэффициент подобия различается по соотношению радиусов окружностей. Также подобны любые квадраты между собой – при коэффициенте подобия, вытекающем из соотношения сторон двух квадратов. Треугольники подобны в двух случаях: если равны все соответствующие углы треугольников, или если стороны пропорционально соотносятся.
Общий принцип подобия фигур в плоской геометрии гласит: луч подобен лучу, прямая подобная прямой, отрезок подобен отрезку, а все углы, при подобии, сохраняются равными.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6628 |
| Номер материала | 602 |