
Методическая разработка "Решение иррациональных уравнений"
Уравнение, содержащее переменную под знаком корня (радикала), называется иррациональным.
Главное при решении иррациональных уравнений состоит в освобождении их от радикалов и сведении к уже изученным нами типам уравнений .
Методы решения иррациональных уравнений:
метод возведения обеих частей уравнения в одну и ту же степень с последующей проверкой;
метод равносильных переходов,
метод введения новых переменных;
графический метод
метод использования монотонности функции
Уравнения вида 1.
К уравнениям такого вида можно применить один из двух методов решения:
возведение обеих частей уравнения в одну и ту же степень, т.е. ()2 2, отсюда 2
метод равносильных переходов
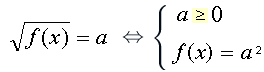
Пример 1. Решить уравнение:
1 способ. Возведём обе части уравнения в 6 степень:
Проверка: (она обязательна)
, т.е. - верное равенство.
Ответ: 67.
2 способ. Применим метод равносильных переходов. Воспользовавшись определением арифметического корня, получим равносильную ему систему:  Первое условие этой системы выполняется при любых значениях х, а второе: х – 3 = 64,
Первое условие этой системы выполняется при любых значениях х, а второе: х – 3 = 64, ![]() х = 67.
х = 67.
Ответ х = 67.
Пример 2. Решить уравнение: ![]()
Упражнение 1. Решить уравнение: 1). ![]() = 2 .
= 2 .
2). ![]() .
.
2.Уравнения вида
К этим уравнениям также можно применить один из двух методов:
возведение обеих частей уравнения в одну и ту же степень, т.е. ()2 = ()2, отсюда = g2(x)
метод равносильных переходов:
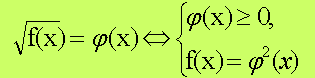
Пример 1. Решить уравнение
Решение. Если применим метод равносильных переходов, то
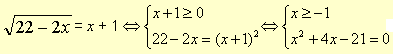
Уравнение х2 + 4х – 21 = 0 имеет корни х=3 и х= -7. Условию х>=-1 соответствует только х = 3.
Ответ: 3.
2 способ. Возведя обе части уравнения в квадрат, получим
22 – 2х = (х + 1)2 22 – 2х = х2 + 2х + 1,
х2 +4х – 21 = 0 х = 3 и х = - 7
Проверка: если х = 3: ; если х=-7:
4 = 4 верно 6 = -6 неверно
Ответ: 3.
В некоторых случаях бывает затруднительно выполнить проверку значений х, найденных на первом этапе решения, подстановкой в данное уравнение.
Пример 2. Решить уравнение: х – Сначала «уединим корень» т.е. приведем к виду : х – 1 = откуда (х – 1)2 = 2х, х2 – 2х + 1 = 2х, х2 – 4х + 1 = 0, откуда х1 = 2 + , х2 = 2 – . Для этих значений х выполнить проверку гораздо сложнее. А выполнение проверки при решении иррациональных уравнений способом возведения обеих частей в одну и ту же степень является обязательным.
Решая это уравнение, используя определение арифметического корня легко проверить, удовлетворяют ли числа 2 + и 2 – неравенству системы х – 1 ≥0, т.е. х ≥ 1. Очевидно 2 + ≥ 1 верно, 2 – ≥ 1 неверно.
Ответ: 2 +
Этот простой пример показывает, что формальное овладение каким-нибудь одним способом решения иррациональных уравнений недостаточно. Надо знать несколько способов решения одного и того же уравнения и уметь выбрать наиболее хороший способ в каждом конкретном случае.
Если в уравнение входят несколько радикалов, то их можно последовательно исключать с помощью возведения в квадрат, получая в итоге уравнение вида .
Пример 3. ![]()
![]()
![]()
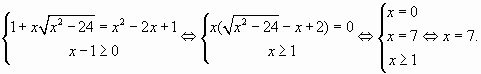
Ответ: 7.
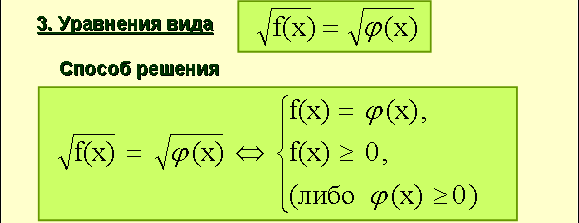

Корнями уравнения х2 – 3х – 4 = 0 являются числа: 4 и -1. Условию х ≥ 3 соответствует только х = 4.
Ответ: 4.
Пример 2. Решить уравнение: ![]()
.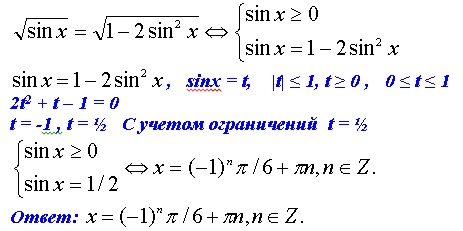
Если встретившиеся Вам уравнение не относится ни к одному из рассмотренных видов, то путем различных преобразовании привести данное уравнение к одному из видов 1, 2 и 3.
4.Уравнения вида ![]()
Пример 1. Решить уравнение ![]() +
+![]() = 4.
= 4.
РЕШЕНИЕ: ![]() +
+![]() = 4.
= 4.
В данном уравнении переменная содержится под двумя радикалами и уединить корни не удается. В таком случае приходится возводить в степень дважды.
(![]() +
+ ![]() )2 = 42
)2 = 42
![]() ,
,
![]()
![]()
![]() получили уравнение вида
получили уравнение вида
Еще раз возведем обе части уравнения в квадрат.
![]()
![]()
![]()
По теореме Виета:
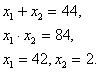
Проверка:
1) Если х=42, то
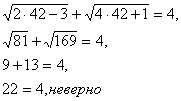
Значит, число 42 не является корнем уравнения.
2) Если х=2, то
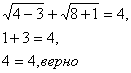
Значит, число 2 является корнем уравнения.
Ответ: 2
Способ II. Метод равносильных переходов.
Иногда удобнее решать иррациональные уравнения, определив область допустимых значении неизвестного (ОДЗ) в самом начале. ОДЗ неизвестного может привести к сужению поиска решения и самому решению уравнения.
Пример 1. Решите уравнение: ![]() +
+ ![]() = 4
= 4
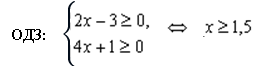
т.е. из двух неравенств следует что ![]()
А уравнение после упрощения примет вид: ![]()
![]()
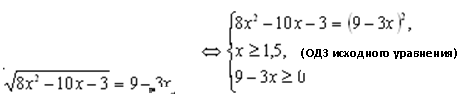
После упрощения уравнение примет вид: ![]()
![]()
![]()
Два неравенства из системы можно записать в виде двойного неравенства: ![]() Из корней х = 2 и х = 42 удовлетворяют этому двойному неравенству только х = 2.
Из корней х = 2 и х = 42 удовлетворяют этому двойному неравенству только х = 2.
Ответ: 2.
Эффективность решения иррациональных уравнений, путем нахождения области допустимых значении неизвестного (ОДЗ) убедительно показывает следующие примеры:
Пример 2. Решите уравнение: ![]() .
.
В данном примере сумма двух неотрицательных корней равна положительному числу. Далее проверяем, существуют ли значения x, при которых оба выражения, стоящие под корнем неотрицательны. ОДЗ: 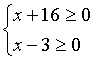 ;
; 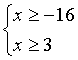 ;
; ![]() .
.
Видим, что такие значения есть. Можно получить решения? Если внимательно посмотреть на слагаемые в левой части уравнения, то можно заметить, что первое слагаемое ![]() при допустимых значениях будет больше 4, да еще плюс второе слагаемое. Таким образом, сумма двух этих слагаемых при допустимых значениях будет больше 4. То есть, решений нет.
при допустимых значениях будет больше 4, да еще плюс второе слагаемое. Таким образом, сумма двух этих слагаемых при допустимых значениях будет больше 4. То есть, решений нет.
Ответ : решений нет.
Пример 3. Решите уравнение: ![]() .
.
В данном уравнении сумма двух неотрицательных корней равна положительному числу. Казалось бы, решения должны быть. Но посмотрим на выражения, стоящие под знаком корня. Оба выражения должны быть неотрицательными, т. е. 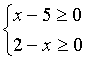 ;
; 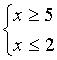 . Мы видим, что оба эти условия не могут выполняться одновременно.
. Мы видим, что оба эти условия не могут выполняться одновременно.
Ответ : решений нет.
Пример 4. Решите уравнение: ![]() .
.
По определению квадратный корень – величина неотрицательная. В данном уравнении сумма двух корней равна 0. То есть сумма двух неотрицательных чисел равна 0. Когда это возможно? Когда оба слагаемых равны 0. То есть, равны 0 выражения, стоящие под знаком корня. Но ![]() при
при ![]() , а
, а ![]() при
при ![]() . Нетрудно догадаться, что не существует такого значения неизвестного x, при котором оба слагаемых будут равны 0.
. Нетрудно догадаться, что не существует такого значения неизвестного x, при котором оба слагаемых будут равны 0.
Ответ: решений нет.
Пример 5. Решить уравнение ![]()
Решение. Сначала найдем ОДЗ переменной, затем корни, решив уравнение. После выясним, какие из найденных корней удовлетворяют ОДЗ В конце выполним проверку для корней входящим в ОДЗ.
ОДЗ: [2; ∞). Возведём обе части уравнения в квадрат, уединим затем полученный радикал и возведём ещё раз в квадрат. Получим корни уравнения 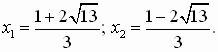
Второй корень х2 не входит в ОДЗ. Поэтому проверку выполним только для х1. После проверки получим корень уравнения 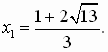
Ответ: 
Пример 6. Решите уравнение:
Анализ показывает, что применение любых способов затруднительно. Попробуем найти ОДЗ.
Таким образом х = 4 – единственно возможное значение.
Проверка.
, 0 = 0 равенство верно.
Ответ: х = 4.

![]()

Пример. Решить уравнение (х2 + 3х) 0
ОДЗ: 2 + х ≥ 0 => х ≥ - 2.
х2 + 3х = 0, или 0
х(х + 3) = 0 или 2 + х = 0
х=0 или х+3=0 или х = -2
х = -3. Но -3 не удовлетворяет условию х ≥ - 2.
Ответ: -2; 0.
Метод введения новых переменных
Мощным средством решения иррациональных уравнений является метод введения новых переменных.(если в уравнений неоднократно встречается некоторое определенное выражение)
Пример.
Обозначим , тогда
а) = t2 и уравнение примет вид:
Корень не удовлетворяет условию
Ответ: 76.
Графический способ решения уравнений
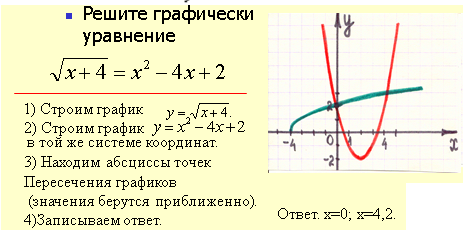
Метод использования монотонности функции
Если f(x) = g(x), а f(x) – возрастает (убывает) и g(x) – убывает (возрастает) или одна из функции константа, то графики этих функции пересекаются в одной точке. Решением уравнения является абсцисса точки пересечения. Уравнение имеет одно решение, которое можно определить подбором.
При этом надо иметь в виду следующее: Сумма двух возрастающих (убывающих) функции есть функция возрастающая (убывающая).
Пример.
Пусть f(x) =. f(x) - возрастает на D(f)= [6/7;∞). g(x) = 2 - константа. Графики функции пересекаются в одной точке. Значит уравнение f(x) = 2 имеет не более одного корня на D(f). Подбором определяем х = 1.

| Автор | |
|---|---|
| Дата добавления | 12.02.2020 |
| Раздел | Алгебра |
| Подраздел | Другое |
| Просмотров | 1603 |
| Номер материала | 6545 |