
Презентация "Движения. Центральная симметрия"

Краткое описание документа:
Презентация «Движения. Центральная симметрия» является наглядным пособием для ведения урока математики по данной теме. С помощью пособия учителю легче сформировать представление ученика о центральной симметрии, научить применять знания о данном понятии при решении задач. В ходе презентации дается наглядное представление центральной симметрии, определение понятия, отмечаются свойства симметрии, описывается пример решения задачи, в которой используются полученные теоретические знания.
Понятие движения является одним из наиболее важных математических понятий. Рассматривать его без наглядного представления невозможно. Презентация – лучший способ наиболее понятно и выгодно представить учебный материал по данной теме. В презентации содержатся иллюстрации, которые помогают быстрее сформировать представление о центральной симметрии, анимация, улучшающая наглядность демонстрации и обеспечивающая последовательную подачу учебного материала. Пособие может сопровождать объяснение учителя, помогая ему быстрее достичь учебных целей и задач, способствуя повышению эффективности обучения.

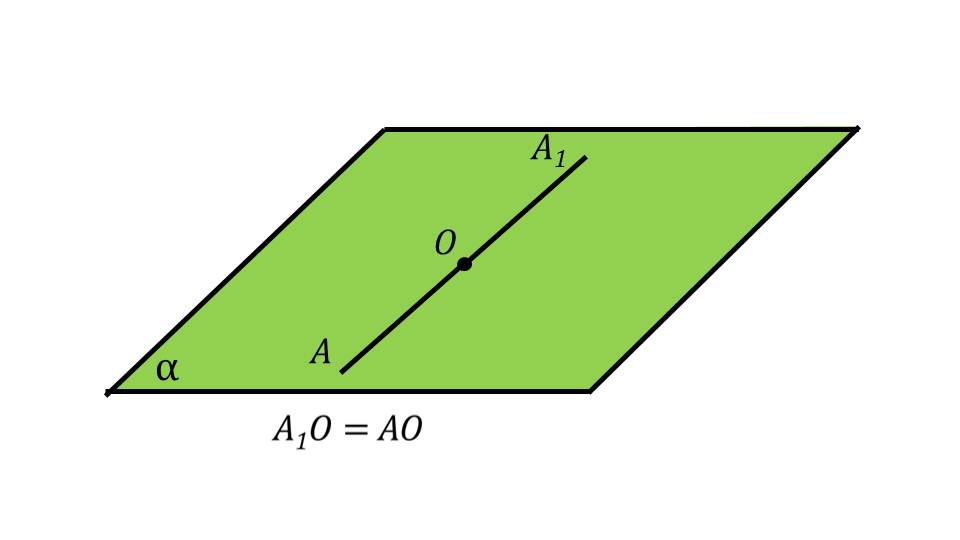
Демонстрация начинается с представления понятия центральной симметрии на плоскости. На рисунке изображена плоскость α, на которой отмечена точка О, относительно которой рассматривается симметрия. От точки о в одну сторону отложен отрезок АО, равный которому А1О отложен в противоположную сторону от центра симметрии. На рисунке видно, что построенные отрезки лежат на одной прямой. На втором слайде понятие рассматривается более детально на примере точки. Отмечается, что центральная симметрия представляет собой процесс отображения некоторой точки К в точку К1 и обратно. На рисунке демонстрируется подобное отображение.
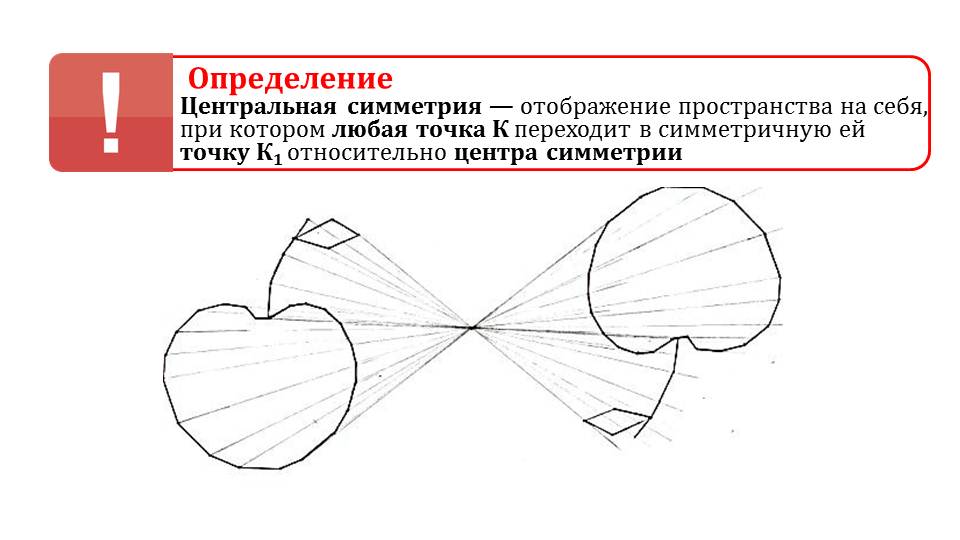
На слайде 3 вводится определение центральной симметрии как отображения пространства, характеризующееся переходом каждой точки геометрической фигуры в симметричную относительно выбранного центра. Определение проиллюстрировано рисунком, на котором изображено яблоко и отображение каждой его точки в соответствующую точку, симметричную по отношению к некоторой точке на плоскости. Таким образом, получаем симметричное изображение яблока на плоскости относительно данной точки.

На слайде 4 понятие центральной симметрии рассматривается в координатах. На рисунке изображается пространственная прямоугольная система координат Оxyz. В пространстве отмечена точка М{x;y;z}. Относительно начала координат М симметрично отображается и переходит в соответствующую М1{x1;y1;z1}. Демонстрируется свойство центральной симметрии. Отмечается, что среднее арифметическое соответствующих координат данных точек М{x;y;z}, М1{x1;y1;z1} равно нулю, то есть (x+ x1)/2=0; (y+ y1)/2=0; (z+z1)/2=0. Это равносильно тому, что x=-x1; y=-y1; z=-z1. Также отмечается, что данные формулы будут верны и при совпадении точки с началом координат. Далее доказывается равенство расстояний, которые между точками, симметрично отраженных относительно центра симметрии – некоторой точки. Для примера указываются некоторые точки А{x1;y1;z1} и В{x2;y2;z2}. Относительно центра симметрии данные точки отображаются в некоторые точки с противоположными координатами А{-x1;-y1;-z1} и В{-x2;-y2;-z2}. Зная координаты точек и формулу для нахождения расстояний между ними определяем, что АВ=√(x2-x1)2 +(y2-y1)2+(z2-z1)2), а для отображенных точек А1В1=√(-x2+x1)2 +(-y2+y1)2+(-z2+z1)2). Учитывая свойства возведения в квадрат, можно отметить справедливость равенства АВ=А1В1. Сохранение расстояний между точками при центральной симметрии свидетельствует о том, что она является движением.
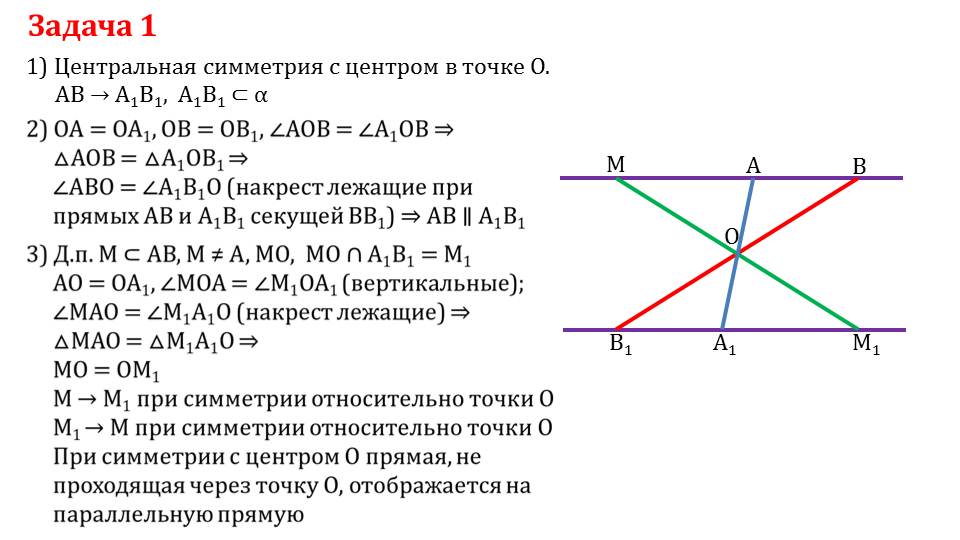
Описывается решение задачи, в которой рассматривается центральная симметрия относительно О. На рисунке изображена прямая, на которой выделены точки М, А, В, центр симметрии О, прямая, параллельная данной, на которой лежат точки М1, А1 и В1. Отрезок АВ отображается в отрезок А1В1, точка М – в точку М1. Для данного построение отмечается равенство расстояний, которое обусловлено свойствами центральной симметрии: ОА=ОА1, ∠АОВ=∠А1ОВ1, ОВ=ОВ1. Равенство двух сторон, углов означает, что соответствующие треугольники равны ΔАОВ=ΔА1ОВ1. Также указывается, что углы ∠АВО=∠А1В1О как накрест лежащие при прямых А1В1 и АВ, поэтому отрезки АВ и А1В1 являются параллельными между собой. Далее доказывается, что прямая при центральной симметрии отображается в параллельную прямую. Рассматривается еще одна точка М, принадлежащая прямой АВ. Так как образующиеся при построении углы ∠МОА=∠М1ОА1 равны как вертикальные, а ∠МАО=∠М1А1О равны как накрест лежащие, а согласно построению отрезки ОА=ОА1, то треугольники ΔМАО=ΔМ1А1О. Из этого следует сохранения расстояния МО= М1О.
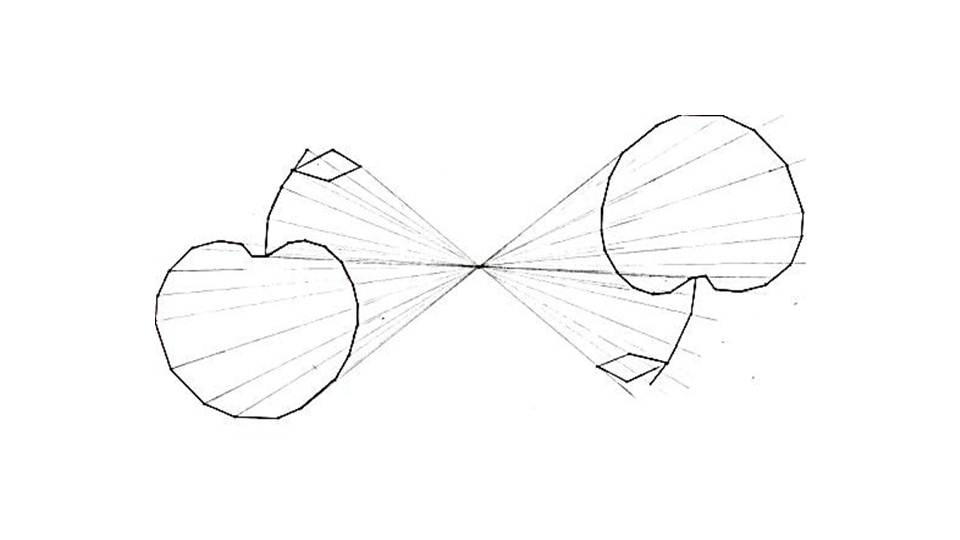
Соответственно, можно отметить переход точки М в М1 при центральной симметрии, и переход М1 в точку М при центральной симме6трии относительно О. прямая при центральной симметрии переходит в прямую. На последнем слайде можно на практическом примере рассмотреть центральную симметрию, при которой каждая точка яблока и все его линии отображаются симметрично, получая перевернутое изображение.
Презентация «Движения. Центральная симметрия» может применяться для повышения эффективности традиционного школьного урока математики по данной теме. Также данный материал может успешно использоваться для улучшения наглядности объяснения учителя при дистанционном обучении. Ученикам, недостаточно хорошо усвоившим тему, пособие поможет получить более четкое представление об изучаемом предмете.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6301 |
| Номер материала | 963 |