
Презентация "Модуль действительного числа и его свойства"

Краткое описание документа:
Презентация «Модуль действительного числа» поможет школьникам при ознакомлении с одним из базовых и необходимых понятий алгебры. Речь идет о понятии модуля.
Как и в предыдущих ознакомительных презентациях, будет даваться определения понятия, его свойства и примеры. На первом слайде приводится обозначение модуля. В качестве действительного числа автор выбрал маленькую латинскую букву «a». Ниже приводится расшифровка модуля на примере некоторых действительных числах.


слайды 1-2 (Тема презентации "Модуль действительного числа и его свойства", определение модуля)
Еще ниже приводится словесная расшифровка этих действий. Также, для лучшего понимания, приводится система, в которой описывается формула раскрытия модуля от неизвестного действительного числа «x».
Следующий слайд содержит в себе множество примеров для закрепления материала. Выполнить эти примеры не составит никакого труда. Главное хорошо понять один раз эту тему, и она запомнится на всю жизнь. Однако, если пропустить данную тему, то в дальнейшем появятся проблемы при решении разных задач, уравнений, при выполнении различных преобразований.
После решения этих примеров, школьники увидят, что модуль любого действительного числа даст в результате положительное число либо ноль. Об этом и других свойствах рассказывается на следующем слайде.
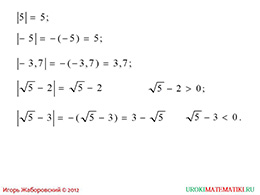

слайды 3-4 (пример, свойства модуля)
Все свойства приведены в виде алгебраической записи, через формулы. О первом свойстве было уже сказано. Второе свойство говорит о том, что модуль в произведении равен произведению от модулей каждого множителя. Чтобы школьники смогли убедиться в правильности этого свойства и запомнить его, им можно предложить решить несколько примеров.
Третье свойство говорит о том, что модуль некоторой дроби равен модулю числителя, деленной на модуль знаменателя этой же дроби.
Далее рассматривается свойство о возведении модуля в квадрат. Так как при возведении в квадрат, да и в любую четную положительную степень, в результате получится положительное число, то можно убрать знак модуля. Опять же, для закрепления этого свойства, можно предложить учащимся пару примеров.
И, наконец, последнее свойство, в котором говориться о том, что модуль некоторого числа является равным модулю противоположного действительного числа.
Благодаря презентации «Модуль действительного числа и его свойства» ученики могут самостоятельно ознакомиться с понятием модуля, увидеть примеры и некоторые важные свойства, необходимые для выполнения преобразований над ними.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5580 |
| Номер материала | 283 |