
Презентация "Метод координат в пространстве. Скалярное произведение векторов"

Краткое описание документа:
Презентация «Метод координат в пространстве. Скалярное произведение векторов» наглядно раскрывает данную тему. С помощью презентации учителю легче сформировать представление о скалярном произведении, научить решать задачи по данной теме. В ходе демонстрации представляется определение скалярного произведения векторов, важные теоремы о скалярном произведении, формулируются свойства скалярного произведения, знания закрепляются решением задач, в которых применяются теоретические сведения о скалярном произведении. Презентация – хороший способ удержать внимание учеников на изучаемом предмете. В презентации наглядность достигается с помощью набора инструментов, которые помогают выделить важные понятия, особенности построения.
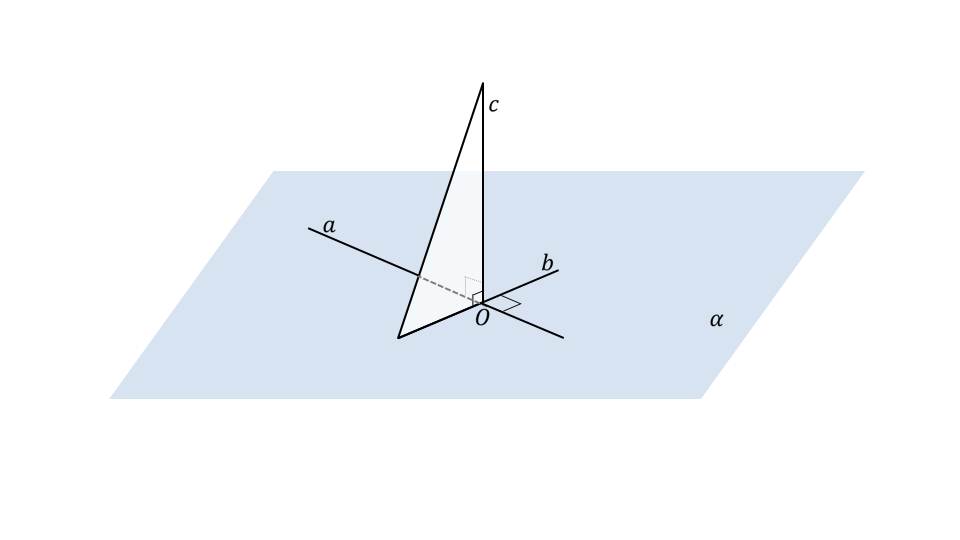
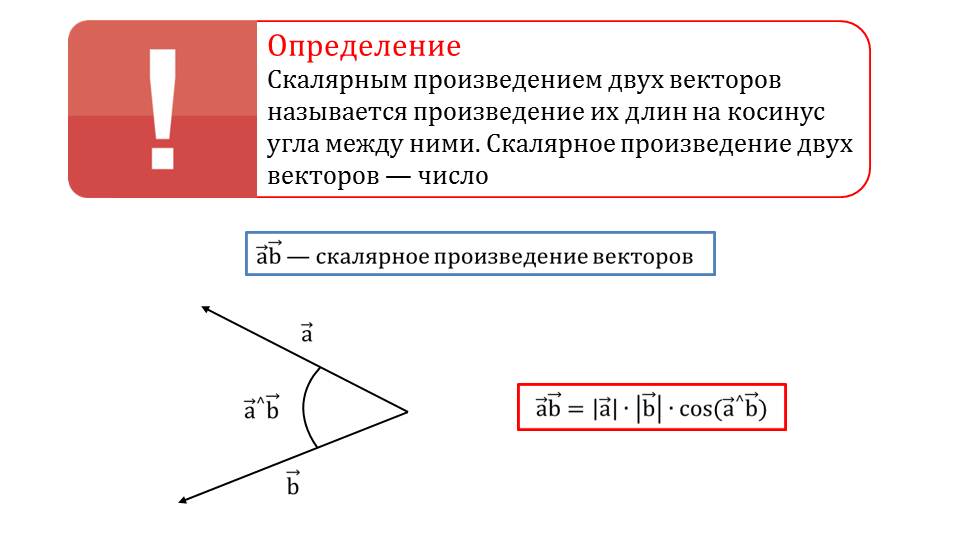
Демонстрация начинается с изображения на плоскости α векторов a¯ и b¯. К плоскости, в которой лежат данные вектора, через их начало проводится перпендикуляр с, который принимается за один из катетов треугольника, где второй катет – вектор b¯. На втором слайде представлено определение скалярного произведения векторов как перемножение их длин на cos угла, который они образуют. Отмечается, что скалярным произведением векторов является обычное число. К определению прилагается изображение векторов a¯, b¯. Отмечается между ними угол a¯^b¯. В рамке выделено нахождение скалярного произведения векторов с помощью обозначений a¯b¯=|a¯|·|b¯|·cos(a¯^b¯).

Слайд 3 демонстрирует теоремы о важных свойствах скалярного произведения. В первой теореме указано, что произведение векторов, не равных нулю, будет нулевым, когда векторы перпендикулярны. Объяснение этого свойства следует из определения скалярного произведения. Косинус угла, образованного между углами, для 90° равен нулю, поэтому и произведение нулевое. Вторая теорема утверждает, что скалярный квадрат вектора равняется квадрату длины этого вектора. Доказать это свойство просто. Между сонаправленными векторами угол 0°. Косинус такого угла cos(a¯^а¯)=1. Поэтому, вычислив формулу, находим a2¯=|a2¯|cos(a¯^b¯)=|a2¯|. В результате получаем a2¯=|a2¯|.


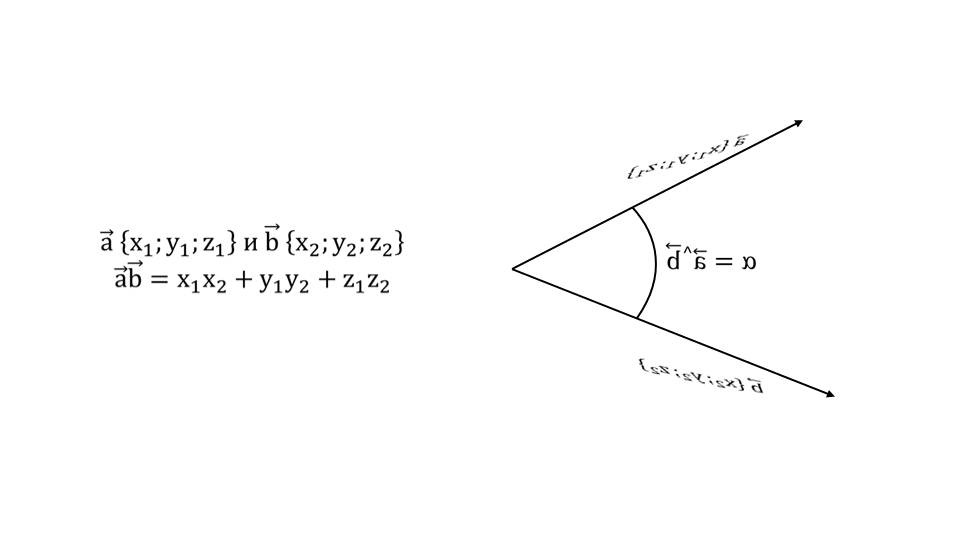
На слайде 4 демонстрируется два вектора aˉ{x1;y1;z1} и bˉ{x2;y2;z2}. Между лучами образуется угол α=a¯^b¯. Скалярное произведение векторов вычисляется перемножением соответствующих координат векторов, суммированием этих произведений.
На слайде 5 представлена формула для вычисления cos между векторами aˉ{x1;y1;z1} и bˉ{x2;y2;z2}. Отмечается, что формула верна для ненулевых векторов cosα= x1x2/√( x12+y12+z12)·√( x22+y22+z22). Описывается доказательство данного утверждения. Зная, что скалярное произведение находится по формуле a¯b¯=|a¯|·|b¯|·cos(a¯^b¯). Из этой формулы следует cosα=a¯b¯/|a¯|·|b¯|. Так как a¯b¯= x1x2+y1y2+z1z2, а модуль вектора представляет собой квадратный корень из суммы квадратов его координат, то |a¯|·|b¯|=√( x12+y12+z12)·√( x22+y22+z22). Подставив полученные выражения для числителя и знаменателя в формулу, находим cosα=x1x2/√( x12+y12+z12)·√( x22+y22+z22).

Основные свойства скалярного произведения представлены на слайде 6. Здесь сформулированы 4 свойства. В первом свойстве отмечается, что квадрат вектора неотрицательное число. При этом если вектор не нулевой, то квадрат вектора – положительное число. Второе свойство демонстрирует переместительный закон произведения векторов a¯b¯=b¯a¯. В третьем свойстве отмечается, что для векторов также справедлив распределительный закон (a¯+b¯)с¯=a¯ с¯+b¯ с¯. В четвертом пункте описан сочетательный закон для векторов k(a¯b¯)=(ka¯)b¯.
Далее рассматривается решение задач, где используются изученные теоретические сведения. На слайде 7 описывается решение задачи 1, где даны векторы a¯, b¯, c¯, k¯. В задаче требуется доказать тождество (a¯+b¯+с¯)k¯=a¯ k¯+b¯ k¯+c¯k¯. В доказательстве применяется распределительное свойство произведения векторов. Если раскрыть скобки, разделив сумму внутри них на два слагаемых, применить распределительное свойство, а затем раскрыть скобки в оставшемся выражении с нераскрытыми скобками, то получаем искомое выражение.
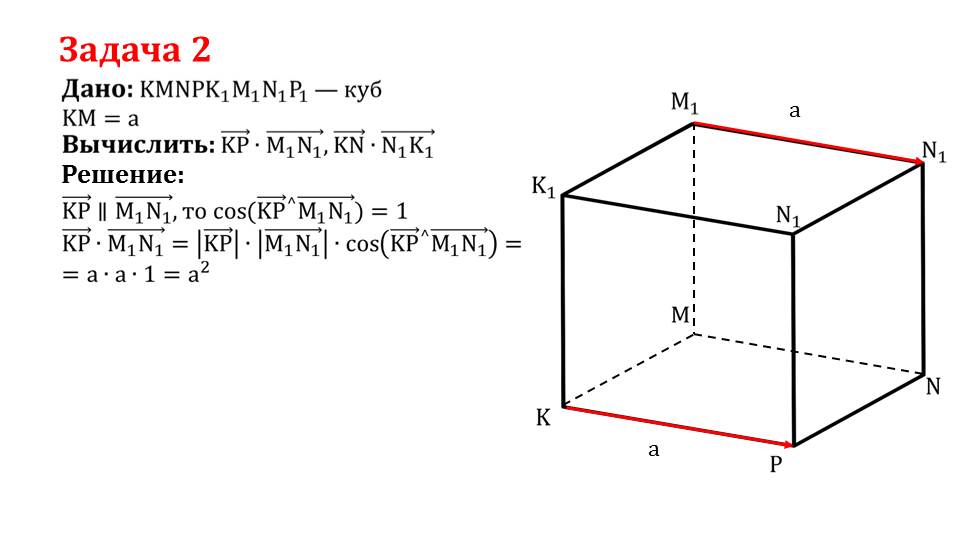
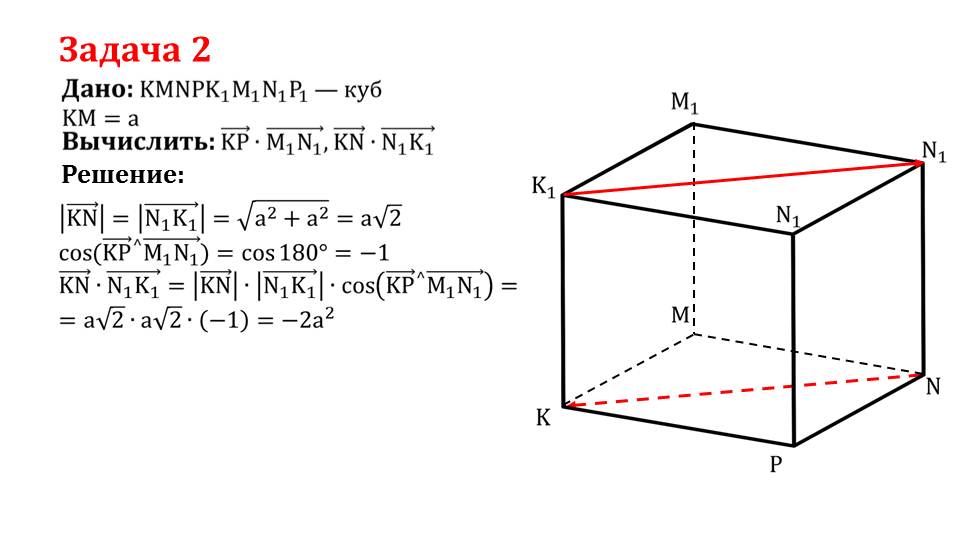
В слайде 8 описывается решение задачи 2, где дан куб KMNPK1M1N1P1 со стороной а. Необходимо вычислить произведение векторов КР¯·M1N1¯, KN¯·N1K1¯. Рядом с условием задачи изображается данный куб. В нем выделены ребра КР¯ и M1N1¯.При решении задачи отмечается, что параллельность векторов КР¯ и M1N1¯ означает, что косинус угла между ними равен 1.Поэтому произведение векторов КР¯·M1N1¯=а2. Продолжение решения представлено на слайде 9. Рассматривается нахождение произведения векторов KN¯·N1K1¯. Это диагонали противолежащих граней куба. Их длины назодятся по теореме Пифагора и составляют а√2. Угол между рассматриваемыми векторами является развернутым, поэтому cos(КР¯^M1N1¯)= cos180°=-1. Используя известные данные, получаем KN¯·N1K1¯=-2а2.

На слайде 10 демонстрируется описание решения задачи 3, в которой даны векторы a¯{1;0;0},k¯{1;√3;0}. Необходимо найти угол между векторамиa¯ и k¯. Пользуясь известной формулой поиска косинуса угла,образованного векторами, и подставляя координаты данных векторов в формулу, находим косинус угла cos(a¯^k¯)= 1·1+0·√3+0·0/√( 12+02+02)·√( 12+(√3)2+02)=1/2. Применяя обратную операцк косинусу, находим угол a¯^k¯=arccos1/2=60°.
В задаче 4, представленном в последнем слайде, даны четыре вектора b¯{3;-5;1},m¯{0;1;-5}, i¯{1;0;0},j¯{0;1;0}. Необходимо найти произведения векторов b¯m¯, b¯i¯, j¯m¯. В решении используется формула нахождения скалярного произведения векторов по координатам. В решении напоминается соответствующая формула. После подстановки значений координат векторов и выполнения вычислений находим значения произведений b¯m¯=-10, b¯i¯=3, j¯m¯=1.

Презентация «Метод координат в пространстве. Скалярное произведение векторов» помогает повысить эффективность традиционного школьного урока по теме за счет улучшения наглядности представления материала. Также презентация поможет быстрее достичь учебных целей и задач учителю, осуществляющему дистанционное обучение. Если ученик недостаточно хорошо усвоил материал на уроке, учитель может рекомендовать данный материал для самостоятельного рассмотрения.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6533 |
| Номер материала | 961 |