
Презентация "Метод координат в пространстве. Связь между координатами векторов и координатами точек"

Краткое описание документа:
Презентация «Метод координат в пространстве. Связь между координатами векторов и координатами точек» наглядно раскрывает связь между координатами векторов и координатами точек. Данный материал является эффективным инструментом для более быстрого достижения учебных целей на школьном уроке. В ходе презентации рассматриваются основные теоремы, которые определяют, каким образом связаны координаты вектора и координаты точек, доказательства этих теорем, описывается решение задач, в которых используются полученные знания. Презентация помогает сформировать представление учеников о предмете изучения, научить их решать задачи по данной теме.
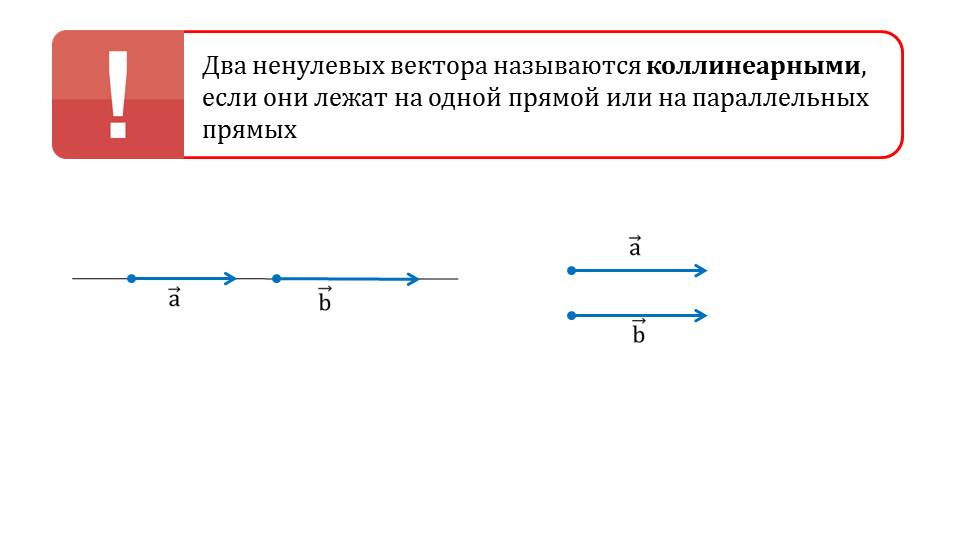
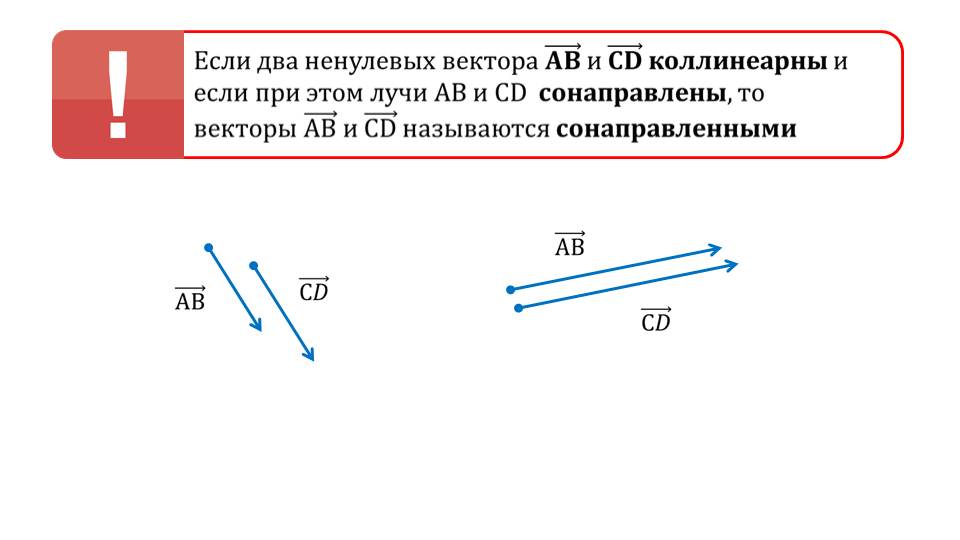
Демонстрация начинается с напоминания понятия о коллинеарности векторов. В рамке выделено определение, в котором указано, что ненулевые векторы являются коллинеарными, когда принадлежат параллельным прямым или одной прямой. Рядом с определением демонстрируется рисунок, на котором изображены коллинеарные вектора a¯ и b¯. На первом рисунке это вектора, лежащие на одной прямой, втором – лежащие на параллельных прямых. Далее напоминается понятие сонаправленных векторов. Отмечается, если векторы АВ¯ и CD¯ коллинеарны и сонаправлены лучи, на которых лежат эти вектора, то векторы являются сонаправленными. На рисунке под определением сонаправленных векторов изображены сонаправленные векторы АВ¯ и CD¯.
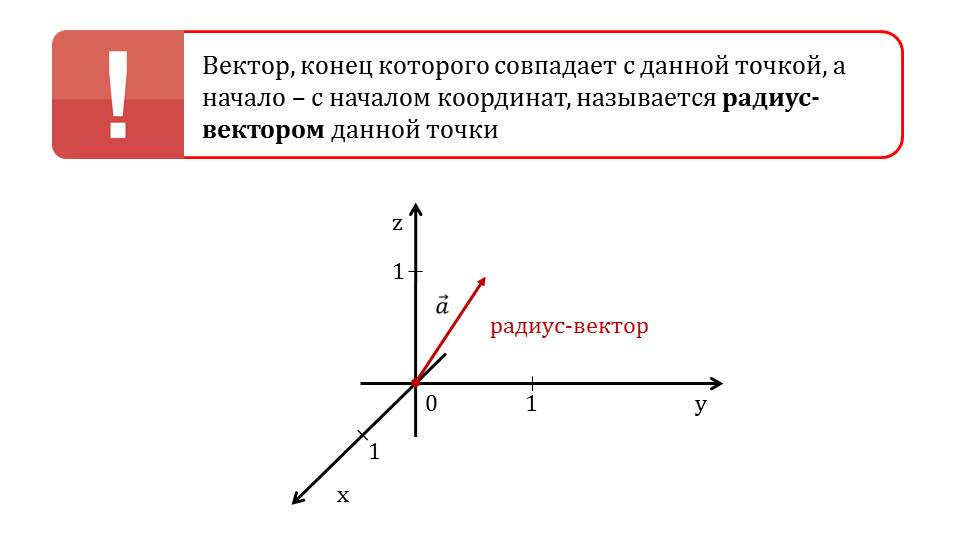
Далее рассматривается понятие радиус-вектора. В рамке выделено определение радиус-вектора, начало которого - начало координат, а конец – данная точка. На рисунке под определением изображена система координат, ее единичные векторы и радиус-вектор ОСˉ.
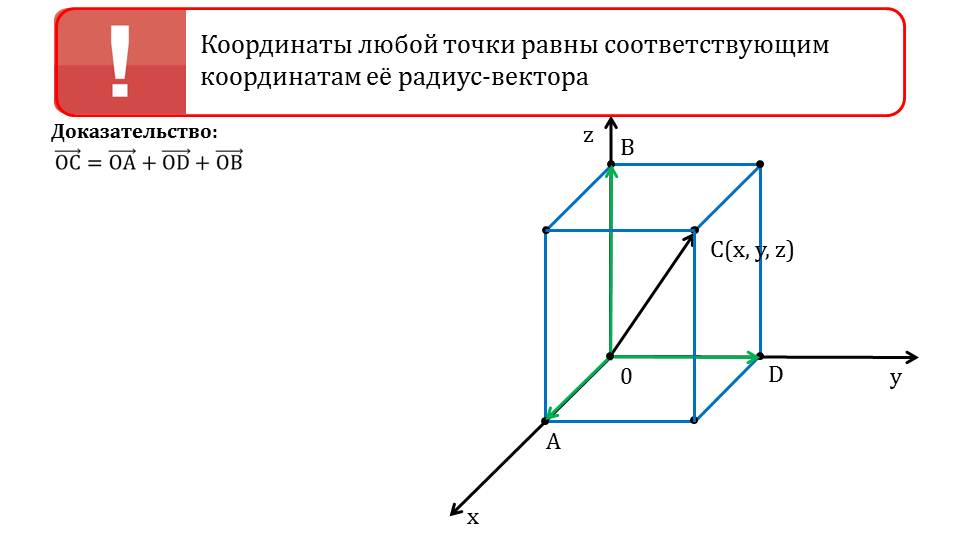
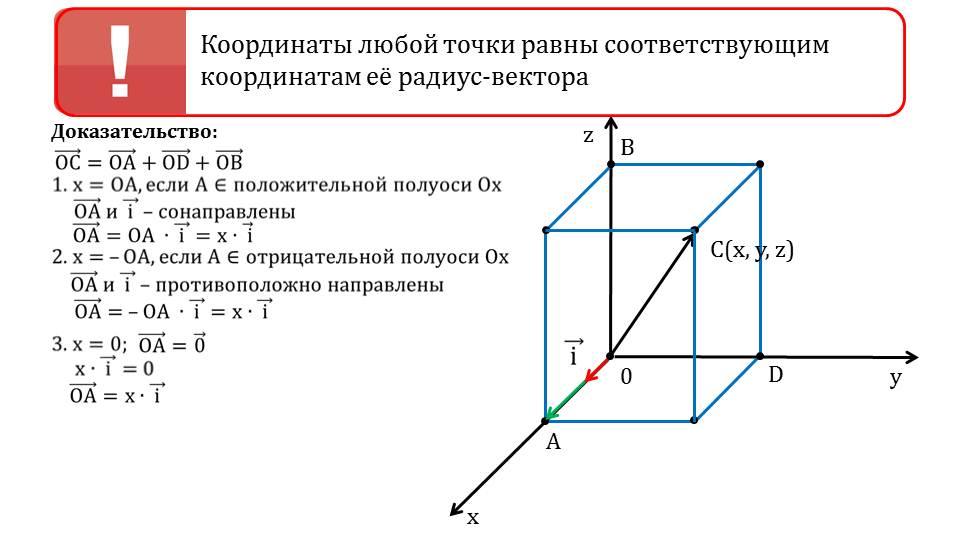
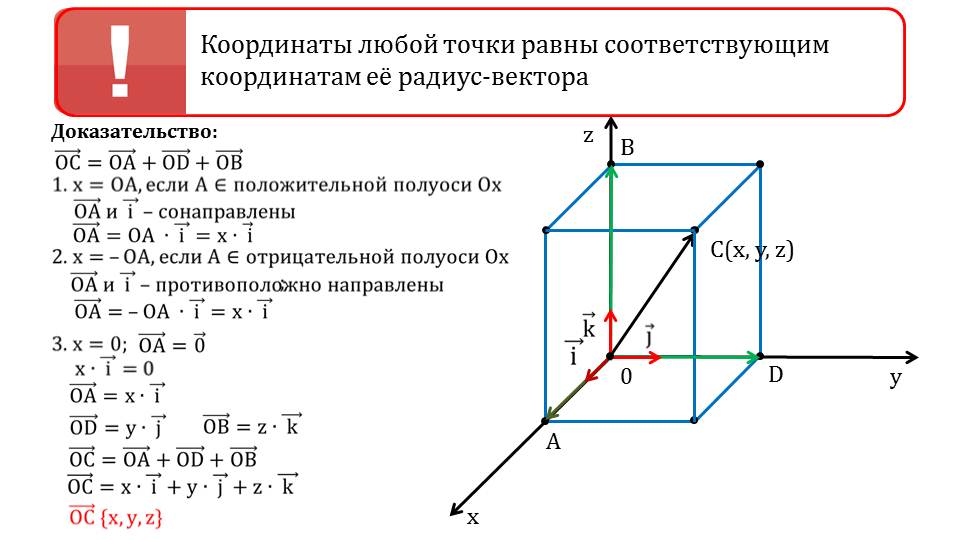
На слайде 4 описывается доказательство положения, в котором утверждается о том, что координаты радиус-вектора и координаты точки его конца совпадают. Под утверждением изображена система координат, в которой отмечена точка C(x;y;z). От начала координат в эту точку проведен радиус-вектор. Построив перпендикуляры к координатным плоскостям, получаем точки пересечения перпендикулярных плоскостей с осями координат – A, B, D. Отмечается, что радиус-вектор - сумма векторов ОСˉ=ОАˉ+ОD¯+ОВˉ. Абсцисса вектора совпадает с длиной вектора ОАˉ. Вектора ОАˉ и координатный вектор iˉ сонаправлены. Поэтому ОАˉ= ОА·iˉ. Если бы А принадлежала отрицательной полуоси Ох, то ОАˉ противоположно направлен с iˉ, и абсцисса ОАˉ=-ОА·iˉ=х·iˉ. Если х=0, то вектор ОАˉ=0ˉ. Таким же образом анализируется ОDˉ=y·jˉ, OBˉ=z·kˉ. Соответственно, разложение радиус-вектора описывается выражением ОСˉ= х·iˉ+ y·jˉ+ z·kˉ. Из разложения вектора следует, что координаты вектора ОCˉ{x;y;z}.
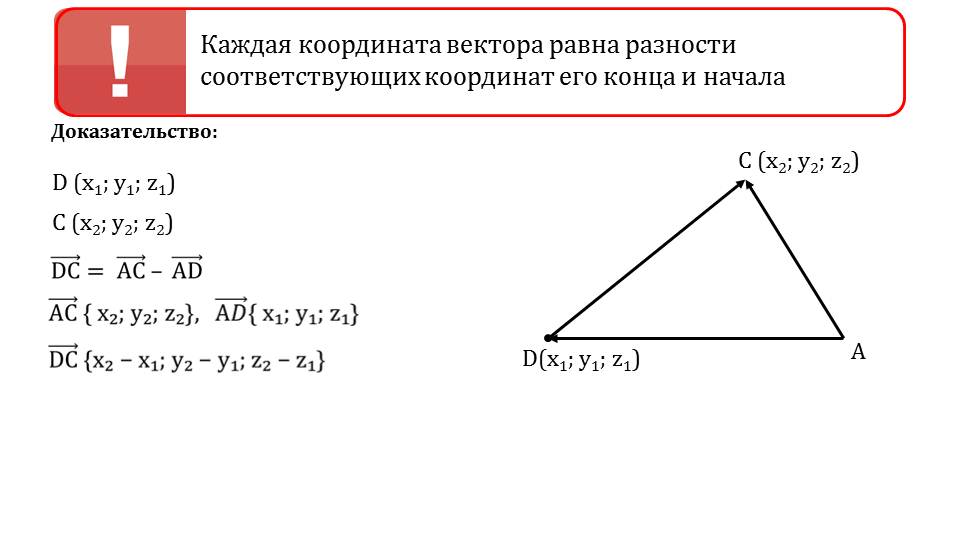
Слайд 7 представляет свойство координат вектора, определяющихся разностью соответствующих координат конца и начала. Для доказательства утверждения приводится пример произвольного вектора DCˉ с координатами начала D(x1;y1;z1) и конца С(x2;y2;z2). На рисунке изображен вектор DC¯ как сумма векторов АD¯ и АС¯. В доказательстве координаты результирующего вектора выражаются через координаты векторов АD¯ и АС¯. Полученные координаты DC¯{x2-x1; y2-y1; z2-z1}.

На слайде 8 рассматривается решение задачи 1, в которой даны точки с координатами А(2;-3;0), В(7;-12;18), С(-8;0;5). В задаче необходимо найти координаты радиус-векторов, концы которых находятся в данных точках. Зная, что координаты радиус-вектора равны координатам точки конца вектора, определяются координаты векторов ОА¯{2;-3;0}, ОВ¯{7;-12;18}, ОС¯{-8;0;5}.
Описывается решение задачи 2, в которой указаны координатных векторов i¯, j¯, k¯, а также векторов a¯, b¯, c¯. В задаче требуется найти координаты векторов, противоположным данным векторам. Тренируясь в нахождении координат векторов, постепенно открываются решения к каждому вектору.

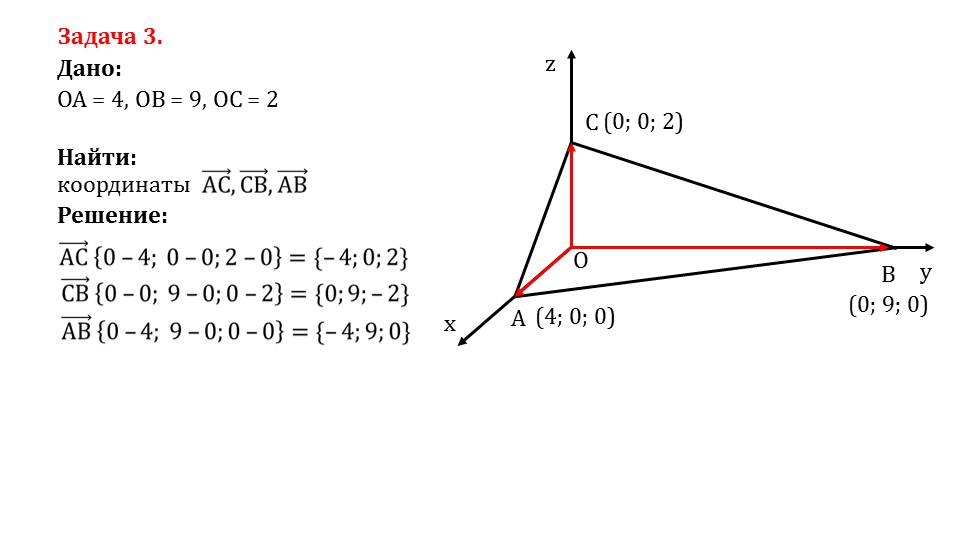
На последнем слайде описывается решение задачи 3, в которой даны векторы ОА¯, ОВ¯, ОС¯. Необходимо найти координаты векторов АС¯, СВ¯, АВ¯. К задаче строится изображение искомых векторов. Пользуясь правилом о нахождении координат векторов, с помощью разности соответствующих координат, находятся координаты векторов.
Презентация «Метод координат в пространстве. Связь между координатами векторов и координатами точек» поможет повысить эффективность традиционного урока математики по данной теме. Наглядность представленного материала поможет лучше объяснить тему в ходе дистанционного обучения. Презентация может быть рекомендована для самостоятельного рассмотрения ученикам, недостаточно хорошо усвоившим данную тему.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 4491 |
| Номер материала | 959 |