
Презентация "Метод координат в пространстве. Угол между векторами"

Краткое описание документа:
Презентация «Метод координат в пространстве. Угол между векторами» представляет наглядный материал по данной теме для урока математики. С помощью презентации учителю легче сформировать у учеников представление об угле между векторами, научить пользоваться теоретическим материалом для решения практических задач по теме. Применением презентации, учитель разнообразит методы ведения урока. Это помогает удержать внимание учеников на процессе обучения. В ходе демонстрации рассматриваются различное взаимное положение векторов, виды углов между ними, приводятся примеры, формирующие предмтавление об угле между векторами, а также описывается решение задач, в которых применяются знания об угле между векторами.
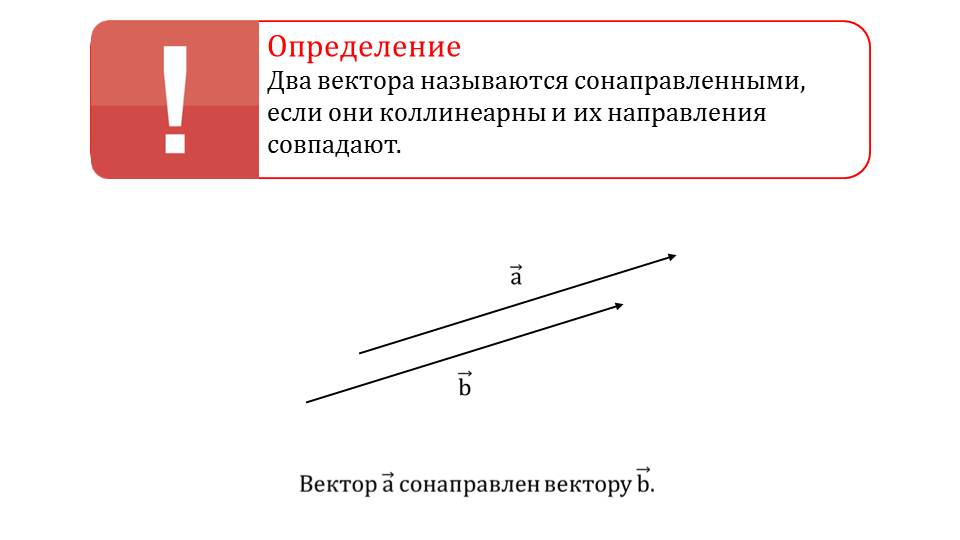
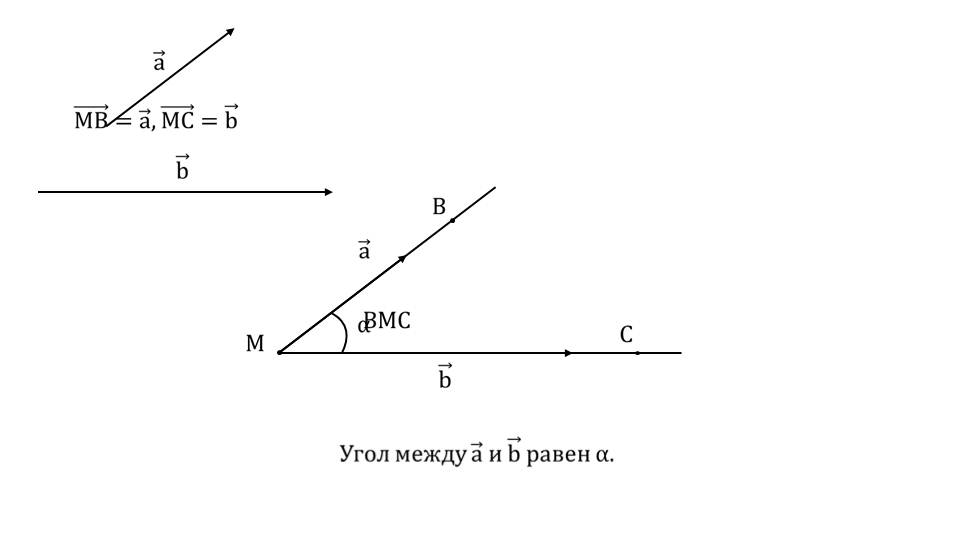
Демонстрация начинается с определения сонаправленных векторов. Отмечается, что два вектора будут коллинеарными, если они сонаправлены и с совпадающими направлениями. К определению прилагается изображение сонаправленных векторов a¯ и b¯. Далее демонстрируется, как найти угол между векторами a¯ и b¯ графически. На рисунке изображены векторы, которые с помощью параллельного переноса изображены с началом в одной точке М. Образующийся при этом угол α между лучами, на которых лежат вектора, является углом между векторами.
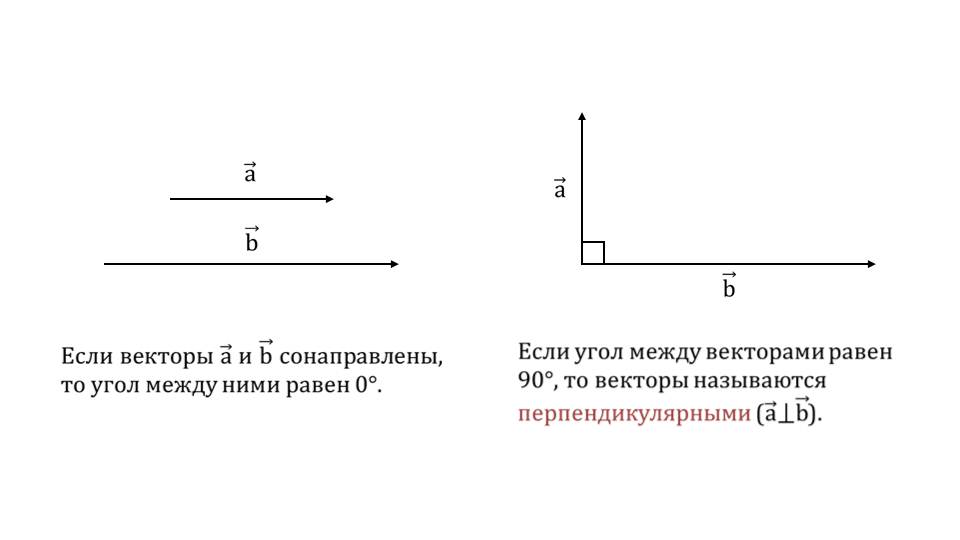
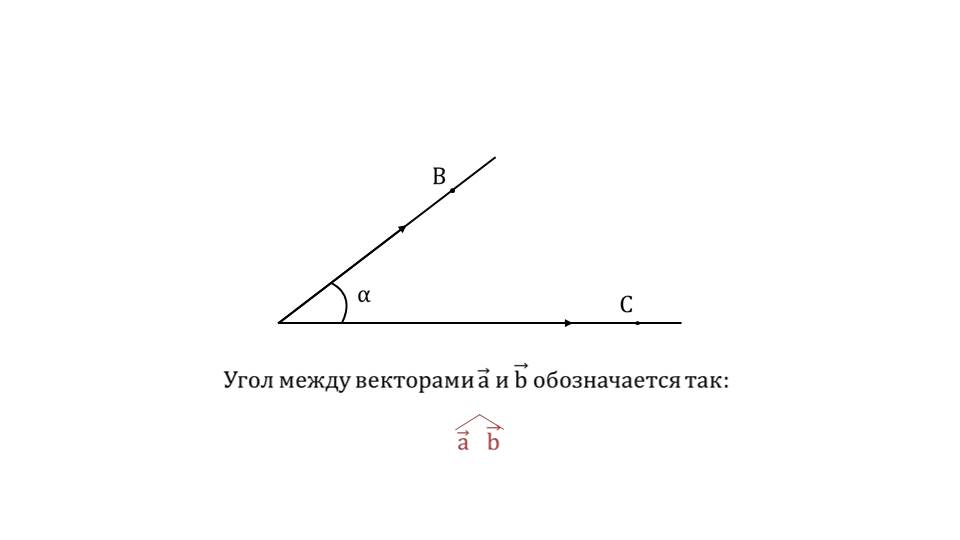
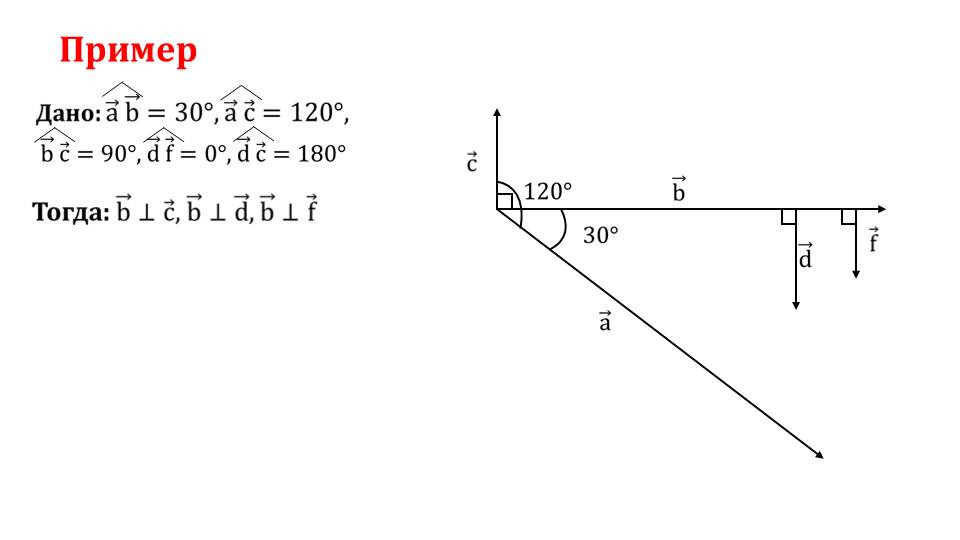
На третьем слайде изображены важные частные случаи расположения векторов – сонаправленные векторы a¯ и b¯ и перпендикулярные векторы. Отмечается, что в первом случае угол между векторами равен 0°, а во втором - 90°. На слайде 4 вводится обозначение угла между векторами a¯^b¯.На рисунке изображены два луча ОВ и ОС, составляющих угол α. Из начала лучей отложены векторы a¯ и b¯. Соответственно, угол между векторами α обозначается a¯^b¯. Примером, помогающим усвоить материал, является изображение нескольких векторов с различными углами между ними. На рисунке изображены векторы a¯, b¯, c¯, d¯, f¯. Между некоторыми векторами образуются острые и тупые углы, есть пример сонаправленных векторов, векторов, составляющих развернутый угол, перпендикулярный угол.
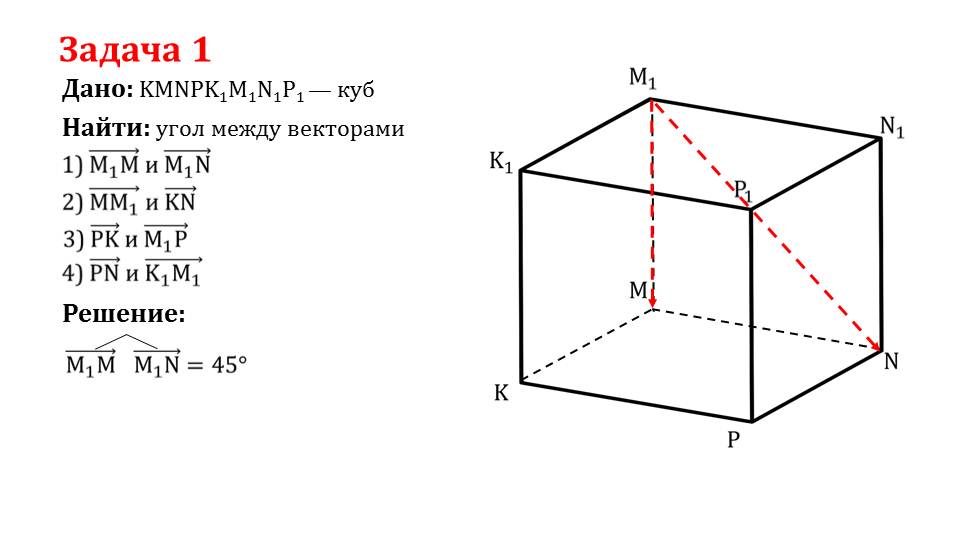
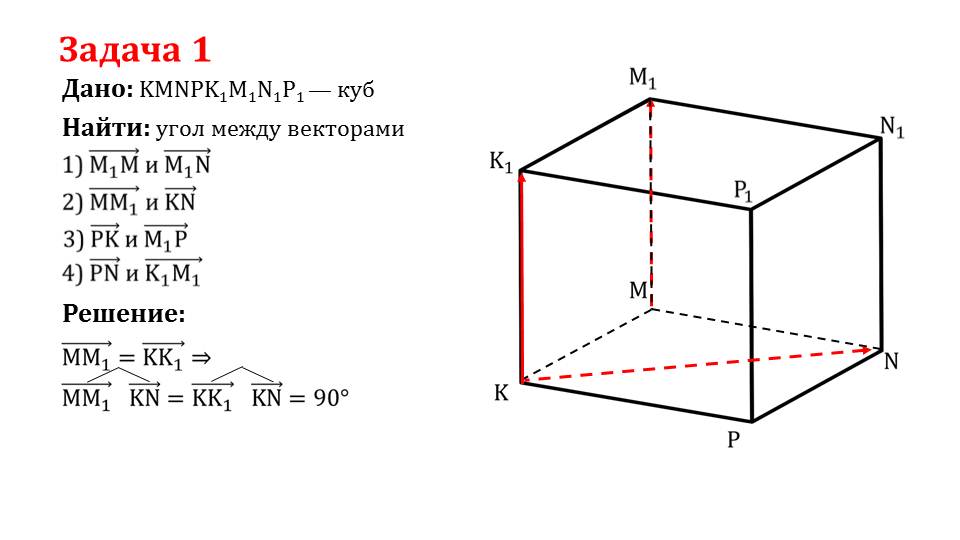
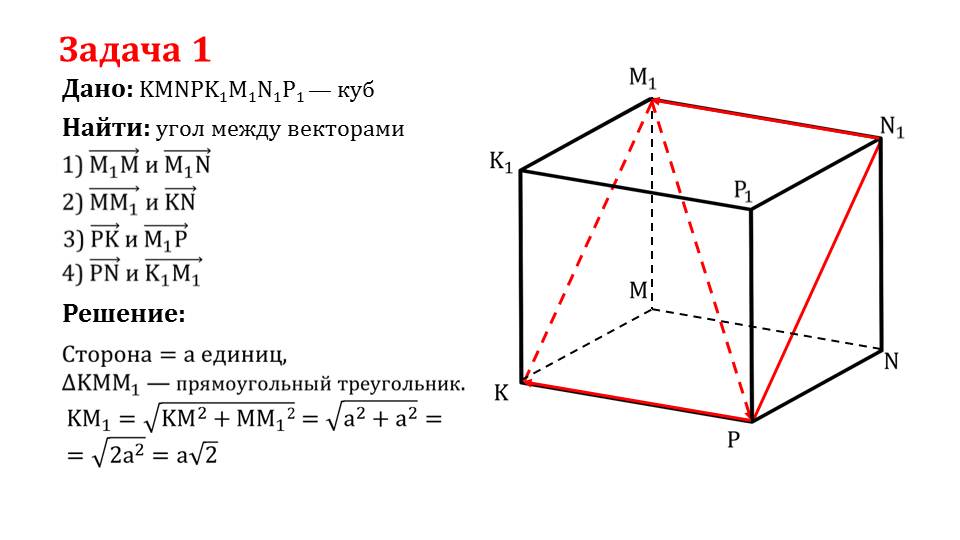
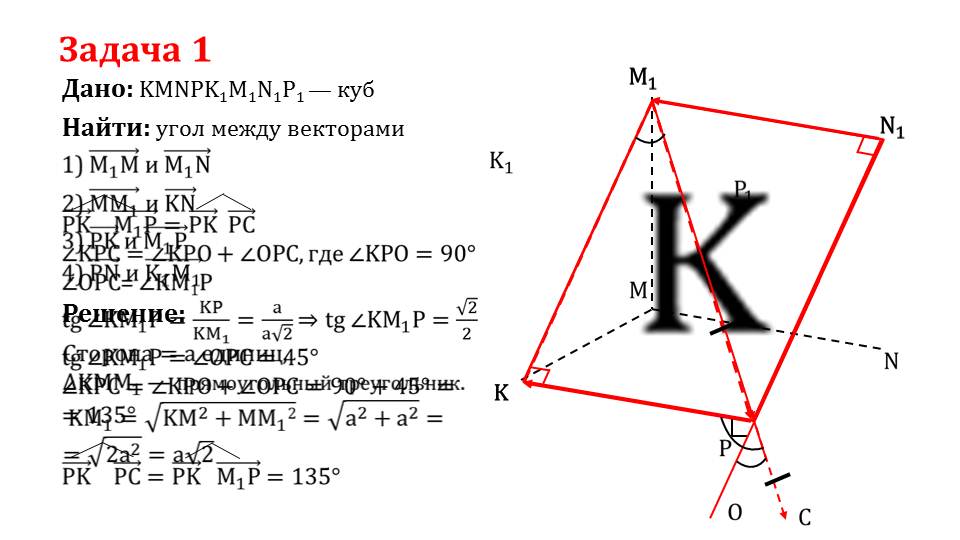
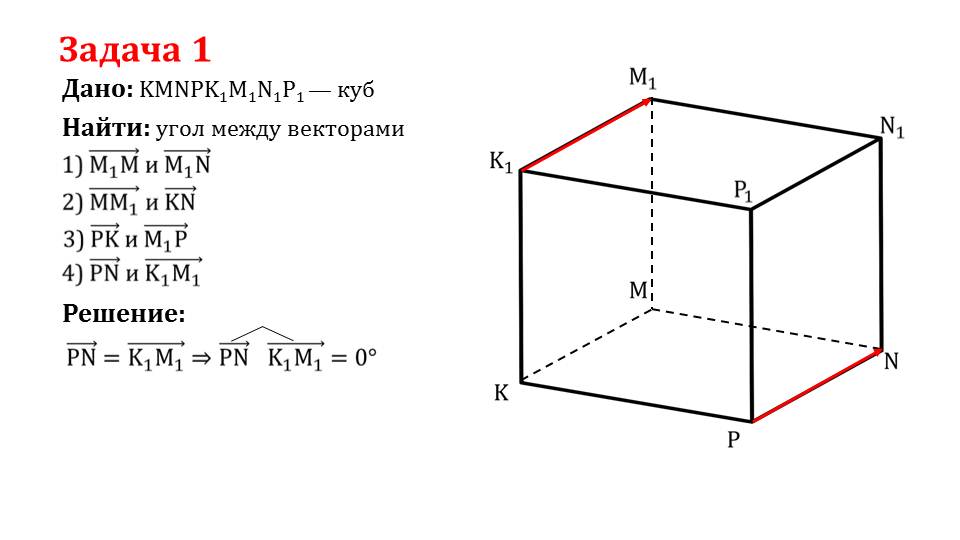
Далее рассматривается решение задачи 1, в которой дан куб KMNPK1M1N1P1. Для него необходимо найти углы между четырьмя парами векторов, которые совпадают с ребрами, диагоналями граней, диагоналями куба. На слайде 6 определяется угол медлу ребром куба и диагональю грани. На рисунке изображен куб, ребро ММ1 и диагональ грани М1N. Угол между соответствующими векторами составляет 45°. На слайде 7 на изображенном кубе выделены КК1 и KN. Из построения очевидно, что угол КК1^KN=90° и ММ1^KN=90°. На слайде 8 для нахождения остальных углов выделены ребра, диагонали граней и диагональ куба, принадлежащие плоскости диагонали куба. Из построенного таким образом прямоугольного треугольника ΔКММ1 определяется дина стороны КМ1=а√2. Пользуясь соотношениями сторон, известными фактами о величине углов в прямоугольном треугольном треугольнике определяются тупые углы, образуемые между ребрами и диагоналями граней РК^РС=РК^М1Р=135°. На слайде 10 отмечаются противолежащие ребра куба. Так как векторы, соответствующие этим ребрам, являются сонаправленными, угол между ними PN^K1M1=0°.
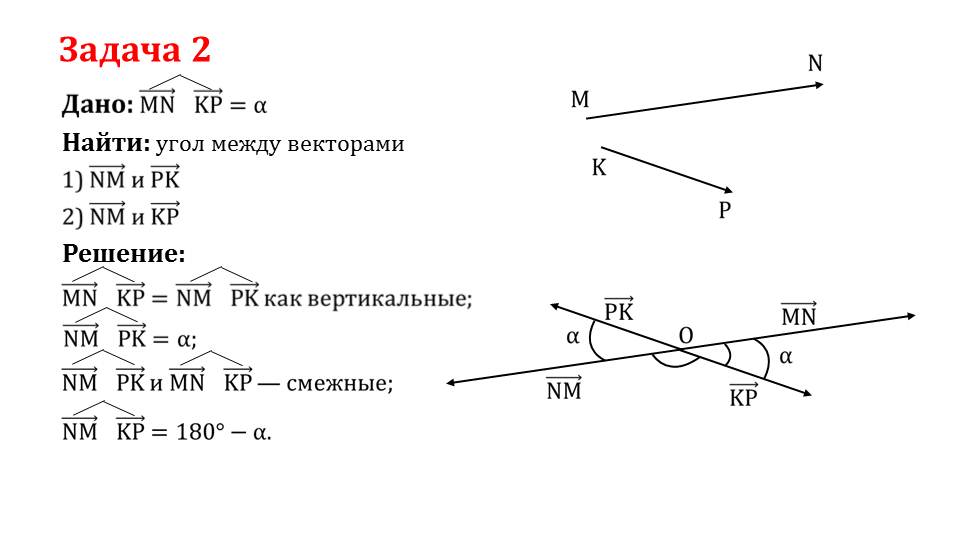
На последнем слайде описывается решение задачи 2, в которой даны два вектора MN¯ и KP¯, и необходимо найти угол между векторами MN¯ и KP¯, MN¯ и PК¯. Для нахождения соответствующих углов векторы перемещаются таком образом, что векторы начинаются из одной точки О. Угол между векторами MN¯ и KP¯= NM¯ и PK¯ равны как вертикальные. MN¯^KP¯=α. При этом из построения видно, что NM¯^PK¯ и MN¯ и KP¯ являются смежными и NM¯^KP¯=180°-α.
Презентация «Метод координат в пространстве. Угол между векторами» может применяться для повышения эффективности урока математики, улучшая наглядность представления материала. Также презентация может помочь достичь учебных целей учителю, осуществляющему дистанционное обучение. Материал может быть рекомендован для самостоятельного рассмотрения ученику, недостаточно хорошо усвоившему тему.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5550 |
| Номер материала | 960 |