
Презентация "Множество действительных чисел"

Краткое описание документа:
«Множество действительных чисел» интересная и обширная тема из школьной алгебры. Так как школьники уже ознакомились с множествами рациональных и иррациональных чисел, то они могут перейти к изучению действительных чисел, ведь они включают в себя и первое и второе множества.


слайды 1-2 (Тема презентации "Множество действительных чисел", определение множества действительных чисел)
Как и любое другое множество, множество действительных чисел имеет буквенное обозначение, - R. Это понятие захватывает все бесконечные и все конечные десятичные дроби. Таким образом, множество всех действительных чисел можно записать как интервал от минус бесконечности к плюс бесконечности, или наоборот, суть от чего не меняется. Эту информацию демонстрирует первый слайд.

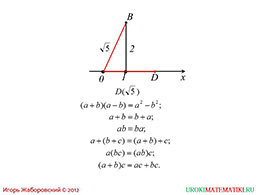
слайды 3-4 (примеры)
Далее, на следующей странице презентации «Множество действительных чисел» приводится текстовая информация. В ней говорится о том, что такое координатная прямая как геометрическая модель, и что такое числовая прямая. Прежде чем давать определение, слайд содержит некоторое предисловие, то есть текст, исходя из которого, можно лучше понять суть определения. Как видно, определения выделены желтым цветом, а само понятие – красным. Это поможет школьникам лучше сконцентрироваться на этом понятии и лучше его визуально запомнить.
Далее, следующая страница, содержит геометрическую запись числовой прямой, то есть – чертеж. Ниже приводятся основные формулы, которые будут очень полезны при преобразованиях или упрощениях громоздких и простых выражений. К ним относятся формула разности квадратов, правило перемещения при сумме и произведения, ассоциативное правило и др. С некоторыми из этих правил, школьники ознакомлены уже в предыдущих уроках по алгебре. Будет полезным вспомнить этот материал.


слайды 5-6 (примеры)
Далее приводятся три основных утверждения, которые школьники могут самостоятельно проверить на примерах.
На следующем слайде дается определение того, в каком случае число «а» будет называться меньше (или больше) некоторого другого числа. Речь идет о действительных числах.


слайды 7-8 (примеры)
Ниже демонстрируются через знаки сравнений случаи, при которых некоторое действительное число «а» (или выражение) является положительным, отрицательным.
На следующем слайде сравнивают некоторое число «а», принадлежащее множеству действительных чисел, с нулем через знаки «больше или равно» или «меньше или равно». Слева написаны сами неравенства, а справа - выводы.
Перейдем к следующему слайду. Он посвящен практическим примерам. В первом примере предлагается сравнить дробное число с целым положительным. Вначале, школьники могут попробовать самостоятельно справиться с примером. Ниже приводится решение.
Второй пример заключается в сравнении суммы рационального и иррационального числа чисел с целым положительным числом. Как видно из решения, при преобразованиях иррациональное число в виде квадратного корня записывается через бесконечную непериодическую дробь.
Третий пример является наиболее простым. Ведь предлагается сравнить отрицательное число с положительным. И вовсе неважно, к каким множествам принадлежат эти числа. Достаточно посмотреть на их знаки.

слайд 9 (пример)
Последний слайд также включает в себя примеры с решениями. Если школьникам удастся разобраться в практических примерах, то они смогут самостоятельно справляться с аналогичными заданиями из домашней работы или самостоятельных и контрольных работ.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 9578 |
| Номер материала | 278 |