
Урок "Уравнения и его корни"

Краткое описание документа:
В предложенном видео речь идет о понятии уравнения и его корнях. Для начала рассмотрена задача о гусях. В задаче стая гусей отвечает гусю, что если бы их было столько, сколько сейчас, да еще столько, да еще полстолька, да еще четверть столько, да еще он, то их было бы сто гусей. Вопрос: Сколько гусей в стае?
Неизвестное число гусей в стае обозначили через Х.
В результате получили: Х + Х +1/2Х+ 1/4Х + 1 = 100.
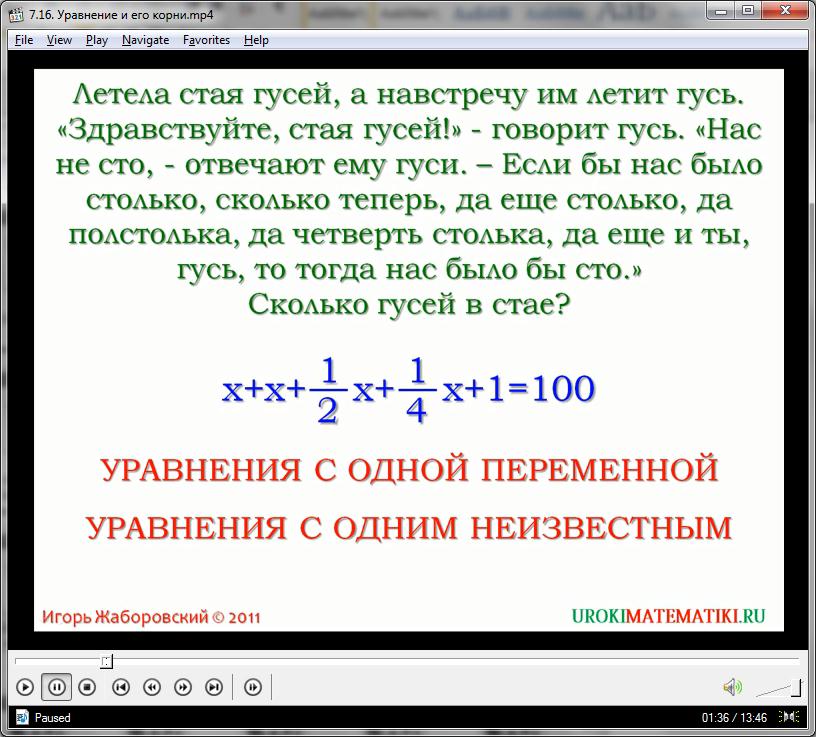
В этом равенстве присутствует неизвестная нам величина Х, значение которой мы ищем. Это значение мы можем найти из составленного нами равенства. Подобные равенства называют уравнениями с одной переменной, или уравнениями с одним неизвестным.
Искомую неизвестную величину принято обозначать буквой Х, хотя можно обозначать любой буквой. Впервые неизвестную величину обозначил буквой и составил уравнение в явном виде с неизвестным древнегреческий математик Диофант в своем труде «Арифметика».
В составленном уравнении необходимо найти такое значение переменной, которое превращает уравнение в правильное числовое равенство. Такое значение неизвестной называют корнем уравнения.
Делаем вывод, что корнем уравнения называется значение переменной, превращающее уравнение в верное числовое равенство. Решить уравнение означает найти множество его корней, число которых может быть различным. Корень может быть один, их может быть несколько, а может и не быть ни одного. В конечном итоге, чтобы решить уравнение, необходимо определить все его корни или убедиться, что у уравнения нет корней.
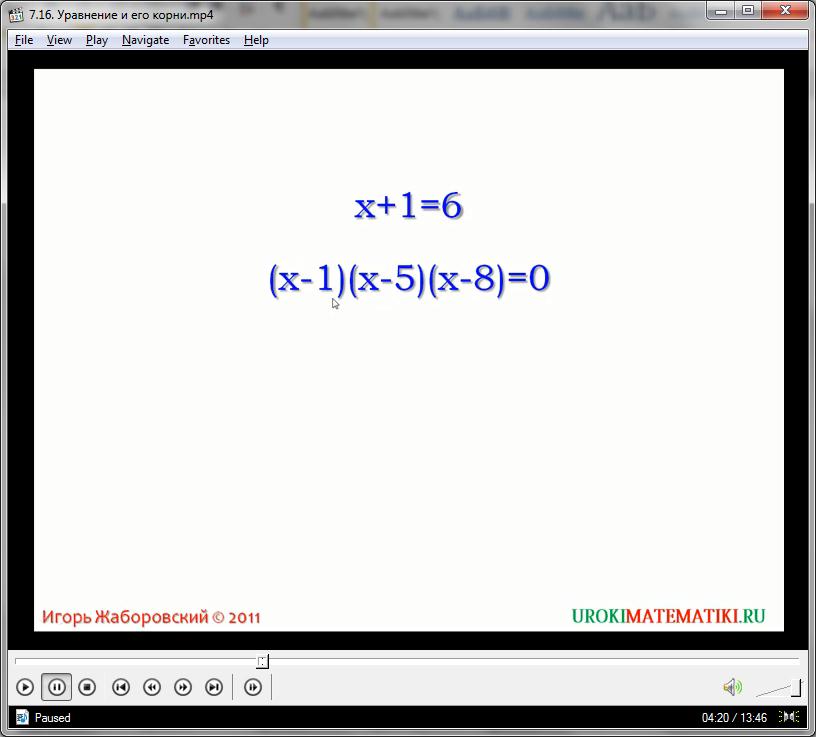
Количество корней уравнения может быть разным в зависимости от вида уравнения. В некоторых случаях и число может быть бесконечным, а может быть равно нулю. Для убедительности автор предлагает рассмотреть примеры уравнений, которые имеют разное количество корней. Это уравнения Х + 1 = 6, (Х – 1)(Х – 5)(Х – 8) = 0, Х = Х + 4, 3(Х + 5) = 3Х + 15. В первом случае корень один, так как только в случае, когда Х = 5, уравнение становится верным числовым равенством 6 = 6. Второе уравнение имеет три корня. Это числа 1, 5, 8. Именно при этих значениях переменной выражения в скобках по очереди принимают значение 0. При умножении на 0 все выражение становиться равным 0. Получаем равенство 0 = 0. Третье уравнение не имеет корней, потому что при любом значении Х правая часть принимает значение больше, чем левая. Четвертое уравнение в свою очередь имеет бесконечное число корней в силу применения сочетательного свойства умножения. После раскрытия скобок и левая, и правая части уравнения имеют одинаковый вид: 3Х + 15 = 3Х = 15.
Далее автор вводит понятие допустимых значений неизвестного. Для этого рассматриваются уравнения 17 – 3Х = 2Х – 2 и (25 – Х)/(Х – 2) = Х + 9. Если в первом случае неизвестное Х может принимать любые значения, то во втором при Х = 2 получаем деление на 0. Следовательно, значения переменной, которые можно подставлять в уравнение в первом случае все числа, а во втором – все числа, кроме 2.
Область определения уравнения – это множество значений переменно, при которых обе части уравнения имеют смысл.
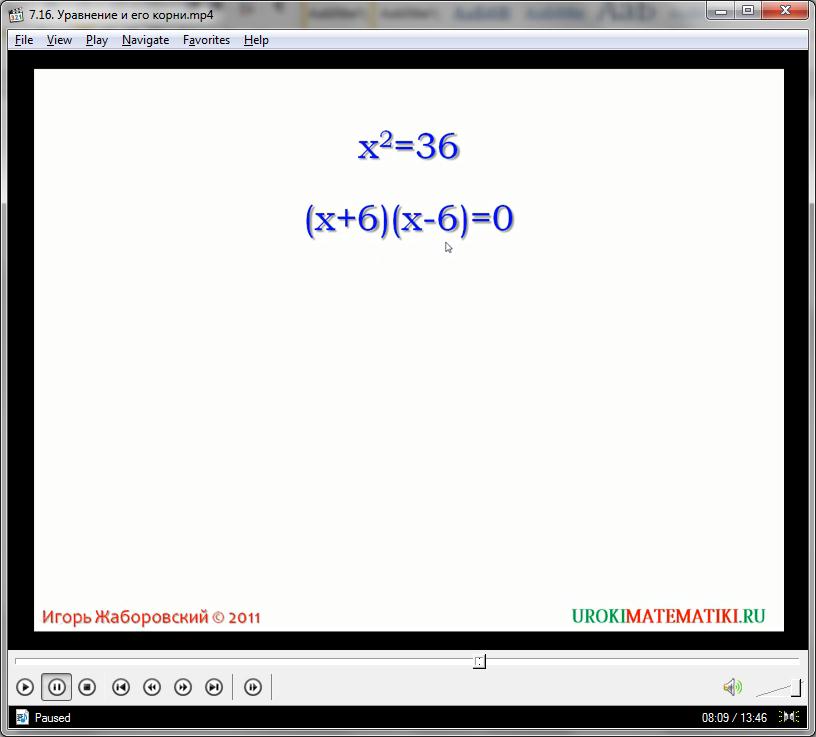
После этого вводится понятие равносильности уравнений. Рассматриваются уравнения Х2 = 36 и (Х – 6)(Х + 6) = 0. У этих уравнений одинаковые корни; такие уравнения принято называть равносильными.
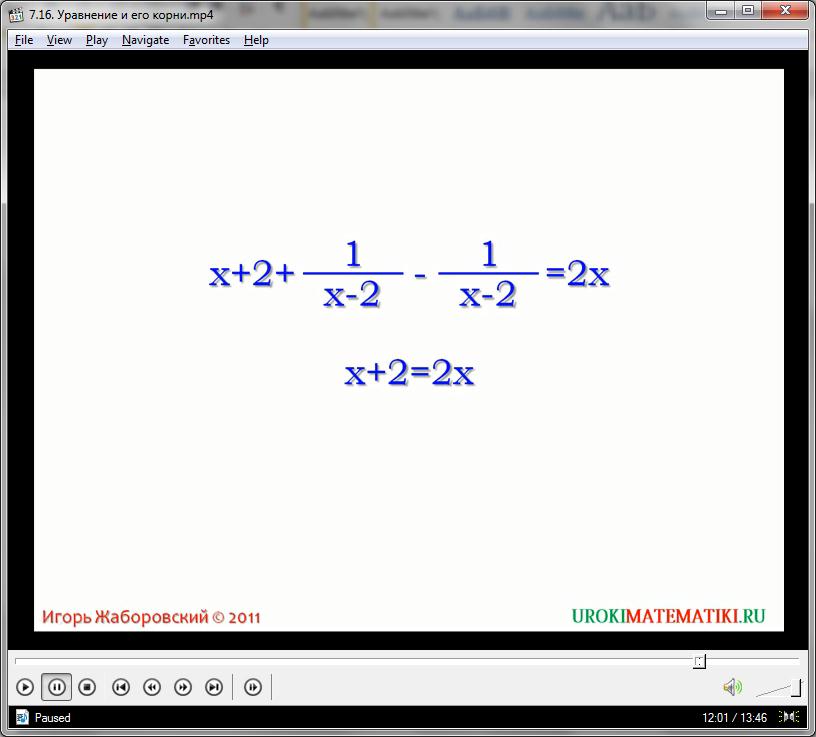
При решении уравнений их заменяют равносильными уравнениями, но более простыми по форме. Необходимо помнить некоторые правила замены уравнения на равносильное уравнение. Во время переноса слагаемого через знак равенства знак слагаемого меняем на противоположный. При умножении или делении обеих частей уравнения на одно и то же число, неравное 0, уравнение останется равносильным. Можно выполнять тождественные преобразования, если они не влияют на область определения уравнения.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5983 |
| Номер материала | 449 |