
Урок "Понятие квадратного корня из неотрицательного числа"

Краткое описание документа:
Дано уравнение x2 = 9. Попробуем решить его графическим способом. Для того, чтобы это сделать, необходимо нарисовать обычную систему координат и построить в ней параболу по формуле y = x2 и прямую – y = 9. Точками пересечения этих графиков будут (-3;9) и (3;9. Значения абсцисс этих точек и будут решением нашего уравнения. Итак, корни уравнения: x1 = -3, x2 = 3.
По аналогии можно решить и подобные уравнения: x2 = 16, x2 = 2, x2 = 25.
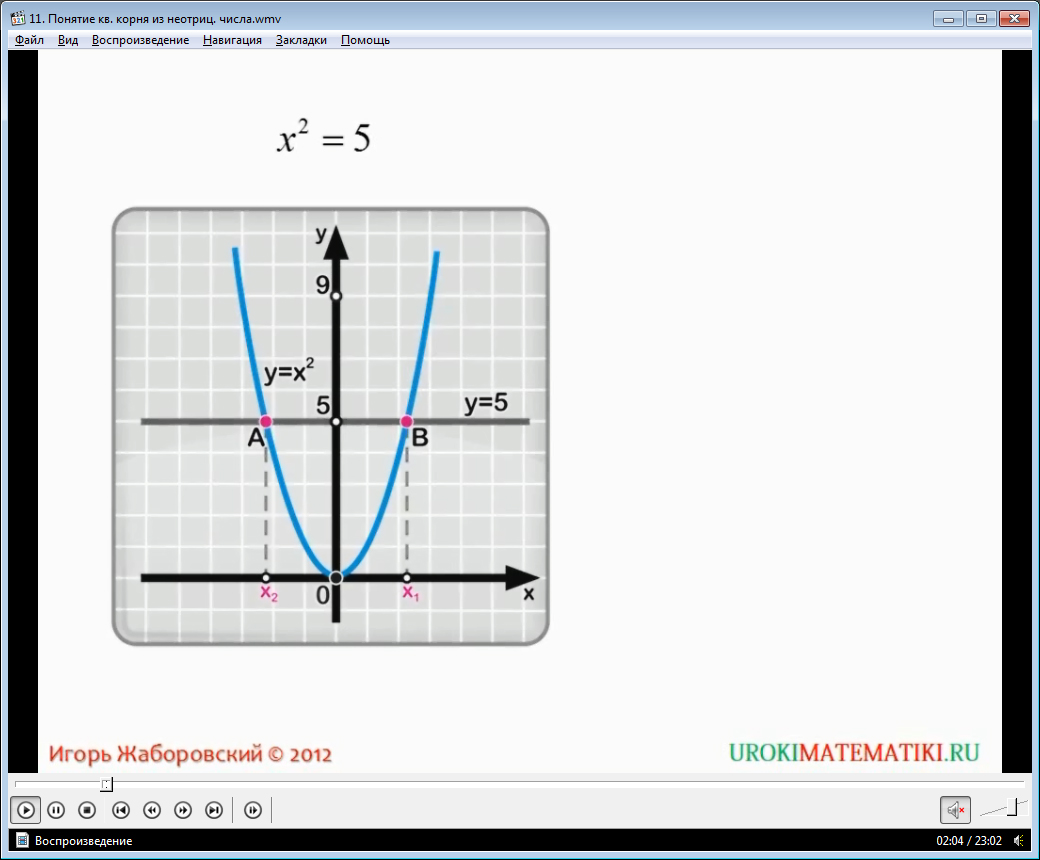
А сейчас давайте попробуем решить такое уравнение: x2 = 6. Естественно, что это уравнение имеет два корня – x1 иx2. По аналогии с вышерассмотренным примером, корни имеют одинаковые значения абсолютных величин, но с противоположными знаками. Использование графика облегчает процесс поиска корней. Воспользуемся им в данном примере. Из графика видно, что один из корней находится левее точки -2, а второй – правее 2. Так что же это за число, квадрат которого равен 6? Однозначно, это не 3, потому что 32 = 9, что определенно нам не подходит. Значит число, которое нас интересует, все-таки, находится в промежутке от 2 до 3. Но в этом интервале находится бесконечное множество рациональных чисел, например, 2,1; 2,0001 и т.д. Может быть, найдется и дробь вида m/nквадрат которой равен 6, тогда вы можете без сомнений написать, что x1 = m/n, x2 = -m/n. Однако, такой дроби, при которой данное равенство (m/n)2 = 6 было бы справедливо, не существует. Доказательство данного утверждения довольно-таки сложное, но необходимо для понимания. Вы можете посмотреть его в видеоуроке.
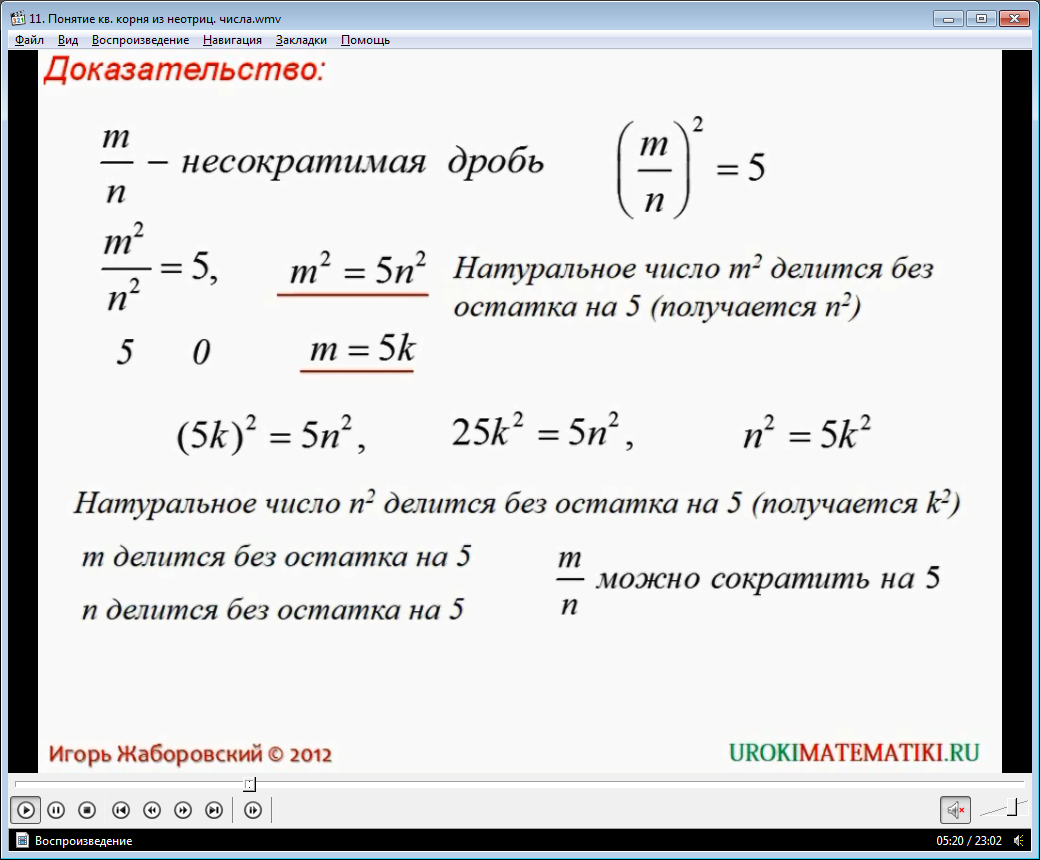
Итак, если вы знаете множество рациональных чисел, то решить уравнение x2 = 6 вам не удастся. Именно для таких случаев и был введен в широкое пользование новый символ √, который называется «квадратным корнем». И благодаря этому знаку вы можете записать решение уравнения как x1 = √6, x2 = -√6. Читать это выражение принято так: «корень квадратный из 6 и минус корень квадратный из 6». Абсолютно у каждого уравнения, которое имеет вид x2 = a, где a > 0, существуют корни, которые записываются √a и -√a.
Следует отметить, что √6 - это не целое и не дробное число. √6- число не рациональное, а из нового иррационального множества. Об этом множестве чисел вы сможете узнать из следующих видеоуроков.
Отметим, что число √6 находится в промежутке числами 2 и 3. 22 = 4, a 32 = 9, потому уточним следующее неравенство: 2,3 < √6 < 2,5. Принято считать, что число √6 равно или 2,44 или 2,45. В результате вы получите приблизительные значения: √6 приблизительно равен 2,44 или √6 приблизительно равен 2,45.
Рассматривая этот способ решения уравнения, вы попадете в типичную для математиков ситуацию, при которой нельзя воспользоваться стандартными приёмами. Выходом из этого положения будет изобретение новых символов и терминов. Проще говоря, следует ввести новое понятие, а после изучить его свойства. Так новый термин и символ закрепляются в математической терминологии.
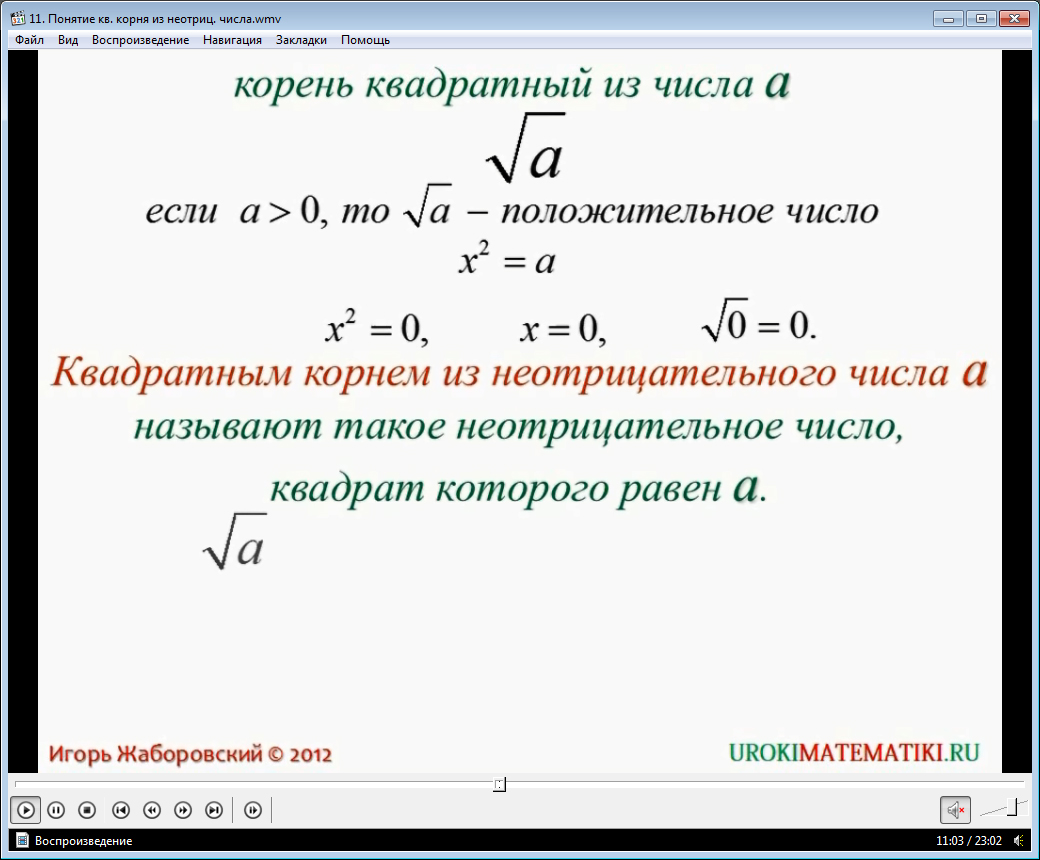
Строгое определение изучаемого вами понятия звучит так: Квадратным корнем из неотрицательного числа a называют такое неотрицательно число, квадрат которого равен a. Его записывают - √а, где называют подкоренным числом.
Следовательно, если a - неотрицательное число, то:
√а больше или равно
(√а)2 = а
Больше информации вы сможете получить из видеоурока.
Рациональные уравнения как математические модели реальных ситуаций
Как вы уже знаете из предыдущих видеоуроков, обычные уравнения могут быть математическими моделями различных ситуаций в реальной жизни. Давайте рассмотрим более подробно пример, при решении которого необходимо ввести рациональное уравнение.
Расстояние между соседними городами составляет 75км. Автобус должен проехать это расстояние, поддерживая постоянную скорость за определенное время, которое оговорено расписанием движения его маршрута. На выезде из первого города водитель попал в пробку и простоял в ней 15 мин. Выехав из нее, ему пришлось увеличить скорость на 20 км/ч, чтобы уложиться в расписание. С какой скоростью должна была быть поездка согласно расписанию?
Решение этой задачи условно можно разделить на несколько этапов.
Этап первый
Составим математическую модель данной ситуации.
Пусть х км/ч– скорость автобуса по расписанию, без учета пробки. Время, которое подразумевает расписание на преодоление расстояния между городами, составляет 75/х ч. Так как водителю пришлось увеличить свою скорость, то время, которое он затратил на переезд, составляет 75/(х + 20) ч. Из двух этих величин, первая больше второй на 15 минут, что составляет ¼ ч.
Составим рациональное уравнение:
75/х = 75/(х + 20) = 1/4.
Таким образом, была составлена математическая модель задачи.
Этап второй
Прежде всего, нам необходимо решить рационально уравнение, которое получилось в конце первого этапа.
75/х – 75/(х + 20) – 1/4 = 0
Приводим к общему знаменателю и упрощаем:
(75(4(х + 20) – 75(4х) – х(х + 20))/(4х(х + 20)) = 0;
(-х2 – 20х + 6000)/(4х(х + 20)) = 0;
Приравняем числитель к 0 и решаем обычное квадратное уравнение:
-х2 – 20х + 6000.
Его корнями являются х1 приблизительно равен 68 и х2 приблизительно равен -88.
Оба эти корня удовлетворяют условие 4х(х + 20) не равно 0. Это значит, что эти значения будут решениями квадратного уравнения.
Этап третий
В вопросе задачи спрашивалось, какова должна была быть начальная скорость согласно расписанию, которую мы приняли за x. Поскольку скорость не может быть отрицательной, то нам подходит значение первого корня. Собственно говоря, это и есть ответ на поставленный вопрос. Скорость, которой должен был держаться водитель согласно расписанию, приблизительно составляет 68 км/ч.
К этой задаче необходимо сделать некоторые пометки:
Ситуация в задаче идеальна. В реальной жизни вряд ли водитель смог бы удерживать одну и ту же скорость на протяжении всего маршрута, на каком-то участке он мог ехать быстрее, а на каком-то - медленнее. В математике такие ситуации сплошь и рядом, и приходится закрывать глаза на это.
Составление математической модели, то есть первый этап, - самый важный. Именно на нем происходит перевод задачи с обычного языка на математический. Это очень ответственная работа, потому что, составив неправильную модель, невозможно получить правильное решение задачи.
Смотрите в видеоуроке подробное рассмотрение аналогичной задачи и других примеров.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7111 |
| Номер материала | 535 |