
Урок "Линейное уравнение с одной переменной"

Краткое описание документа:
Для рассмотрения представлено видео по теме «Линейное уравнение с одной переменной». Рассказ основан на исторических фактах, запечатленных в древнеегипетском папирусе, который хранится в Московском музее изобразительных искусств имени Александра Сергеевича Пушкина. Речь идет о так называемом Московском папирусе, созданном около 2 тысячи лет до нашей эры в Древнем Египте.
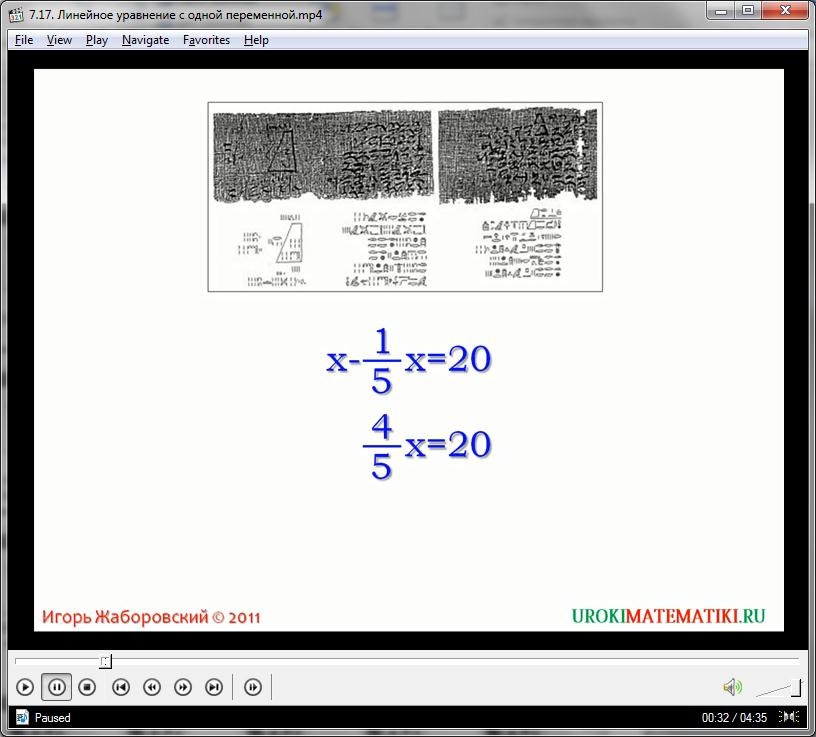
В папирусе описаны многие факты. Но одна из задач сводится к решению уравнения Х – 1/5Х = 20. Это уравнение, в свою очередь, равносильно уравнению 4/5Х = 20. Рассмотрим равносильность более подробно. Известно, что в записи Х подразумевается 1Х. Это выражение в свою очередь преобразуем для удобства к виду 5/5Х. В результате получим уравнение 5/5Х – 1/5Х = 20 или 4/5Х = 20.
Уравнения такого типа решали в Древнем Египте, Вавилоне, Древней Индии и Древнем Китае еще 2 тысячи лет до нашей эры.
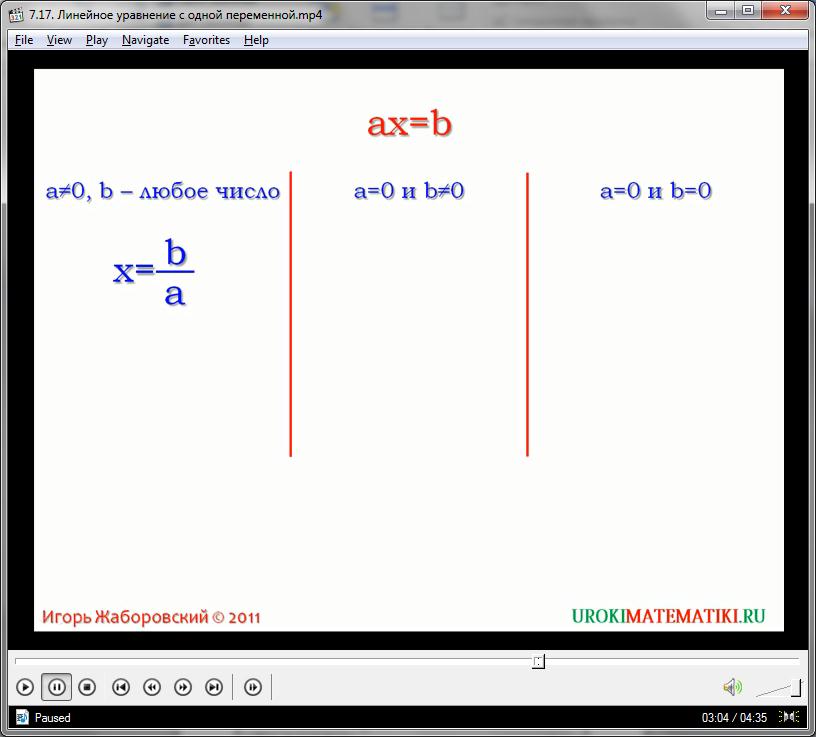
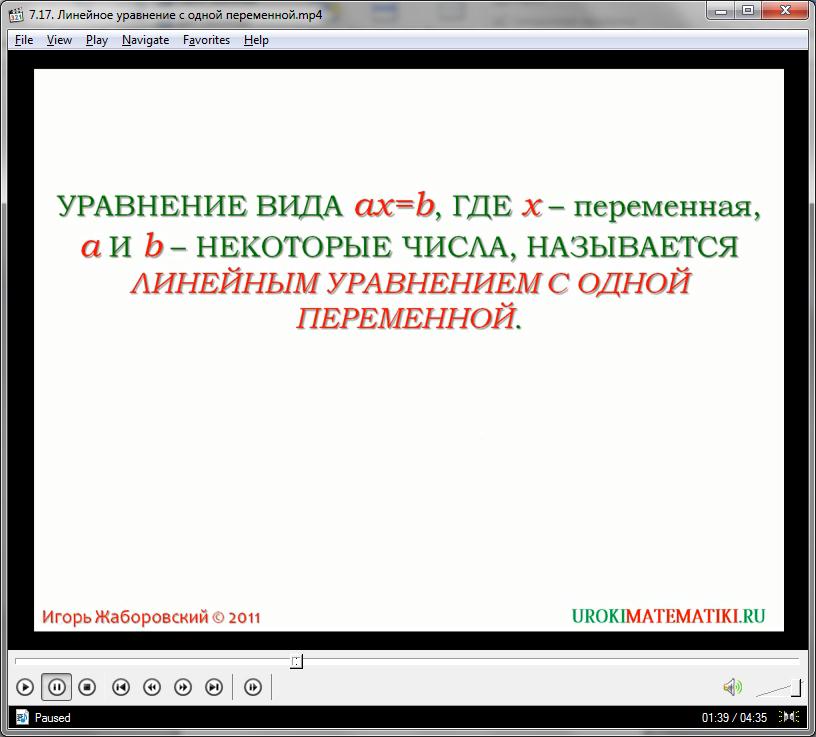
Уравнение 4/5Х = 20 имеет вид ax=b. В уравнениях такого типа a и b могут быть любыми числами. В случае данного уравнения a равно 4/5, а b – 20. Уравнения такого вида называют линейными уравнениями с одной переменной. Получим определение: Уравнение вида ax=b, где x переменная, a и b некоторые числа, называется линейным уравнением с одной переменной.
Примерами линейных уравнений с одной переменной могут служить уравнения, предложенные в рассматриваемом видео: 0,5Х = 2 (в этом случае а равно 0,5, b равно 2), 7Х = 0 (а равно 7, b равно 0), -Х = 4 ( а равно -1, b равно 4).
В уравнении ax=b число a называют коэффициентом уравнения, а число b свободным членом.
Следующий момент, рассмотренный в видео, это вопрос количества корней линейного уравнения. Для нахождения ответа на этот вопрос рассмотрены три случая. Первый, когда a не равняется 0 и b – любое число. Второй, когда a равняется 0 и b не равняется 0. Третий, когда a равняется 0 и b равняется 0.
В первом случае, если a не равно 0, разделим обе части уравнения на a. Получим, что x = b/a, так какax/a=x, а b/a=b/a. В этом случае уравнение такого типа имеет единственный корень и это b/a.
Второй случай имеет вид 0x=b. Такое уравнение не может иметь корней. Ведь любое из чисел при умножении на 0, будет равно 0. Получится что 0 равен числу b. А по условию b не равно 0. Значит, равенство не будет выполняться ни при каких значениях x.
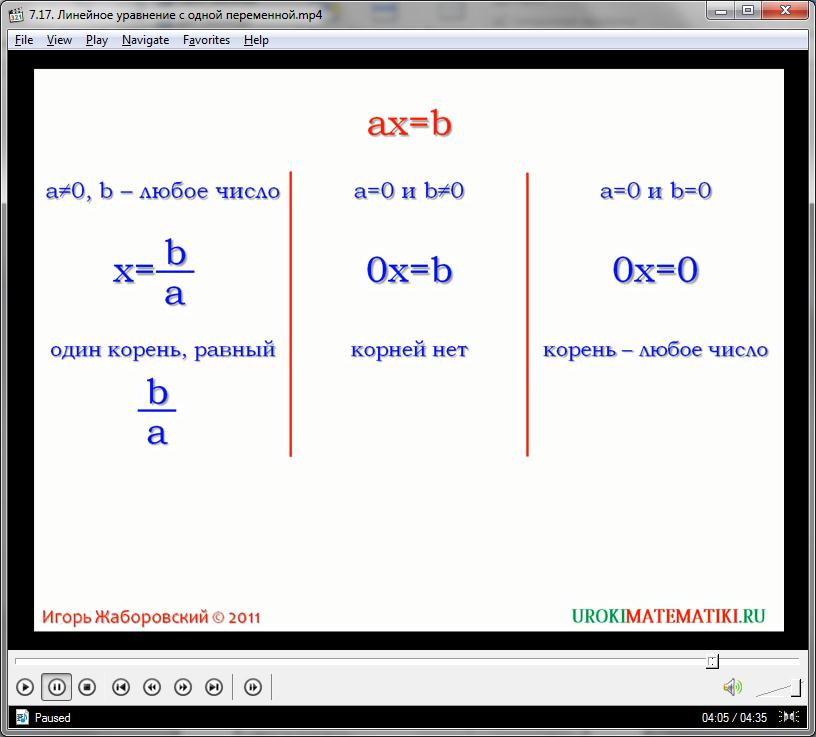
Третий случай представляет собой уравнение 0x=0. Множество решений такого уравнения будет бесконечным. Любое число, умноженное на 0, равно 0, следовательно, равенство будет выполняться при любых значениях переменной x. В этом случае от значения х не зависит ничего.
Можно сделать вывод, что множество корней линейного уравнения с одной переменной может составлять один элемент, как в первом случае, может быть пустым, то есть не иметь корней, во втором – либо быть бесконечным как в третьем случае, когда число корней бесконечно.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4500 |
| Номер материала | 450 |