
Презентация "Понятие квадратного корня из неотрицательного числа"

Краткое описание документа:
На этом уроке школьники познакомятся с таким понятием, как квадратный корень. Эта тема является одной из важных и базовых в курсе алгебры. Данная презентация посвящена арифметическому квадратному корню. Благодаря этому ресурсу понять суть этой темы будет несложно. Ведь каждое текстовое утверждение сопровождается иллюстрациями, графиками и примерами.

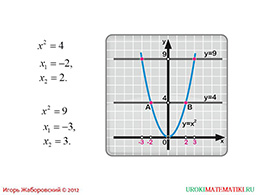
слайды 1-2 (Тема презентации "Понятие квадратного корня из неотрицательного числа", пример)
Итак, презентация начинается со знакомой уже многим школьникам, параболы на координатной оси. При этом школьники могут увидеть значения абсцисс и ординат. На графике видно, что значения ординат при различных значениях иксов являются его квадратом. То есть, например, при х =2 (или -2), значение функции в этой точке будет 4.
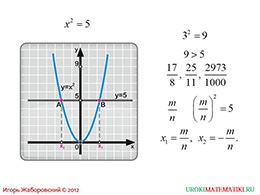

слайды 3-4 (пример, доказательство)
На следующем слайде, на примере этой же параболы, предлагается найти значение абсциссы, при значении ординаты, равной 5. Следовательно, нужно найти такое число, которое, при возведении в степень 2 будет равно 5. Графически найти это значение не составит никакого труда. Необходимо построить прямую y = 5, а далее – найти точки пересечения с нашей параболой. Но алгебраическими методами найти это значение (или значения) будет невозможно.
Следующий слайд заключается в доказательстве некоторого утверждения. Суть ее в следующем. Для начала x приводится в виде некоторой дроби, где и в числителе и в знаменателе натуральные значения. Дробь эта является несократимой. Если мы ее подставим вместо абсциссы в предыдущее выражение, где требовалось найти такое значение абсциссы, при котором ее квадрат будет равняться пяти, то, выяснится, что такая дробь не существует. Доказывается это очень просто. Собственно и это доказательство демонстрируется на данном слайде.


слайды 5-6 (метод доказательства от противного)
Раз дело коснулось доказательств, то на следующей странице приводится определение такого выражения, как «доказательство от противного». Что это такое, и с чем его едят, можно прочитать на этом слайде.
Вернемся к нашей проблеме. Так как алгебраически найти некоторое число, которое в квадрате даст нам 5, невозможно, был придуман знак арифметического корня. Как он записывает и как с ним работать будет демонстрировано на данном слайде. При этом, так называемое, подкоренное выражение, должно быть больше либо равно нулю. Если подкоренное выражение будет больше нуля, то, следовательно, корень от этого числа будет иметь также положительное значение.
Если подкоренное число будет отрицательным, то найти такое число, которое в квадрате даст неотрицательное число будет невозможным. Это говорит о том, что при решении уравнений, которые содержат переменные в подкоренном выражении, необходимо проверить условие его положительности.


слайды 7-8 (определение квадратного корня)
Далее школьники будут ознакомлены с понятием «извлечение квадратного корня». Дается определение понятным текстом, после чего приводится таблица, в которой с одной стороны демонстрируются примеры возведения степеней, с другой стороны – обратный процесс, то есть извлечение корня. Если есть возможность продемонстрировать данную презентацию на уроке, то учащимся можно предложить самостоятельно решить эти примеры, либо привести похожие.
Эта презентация, как и все остальные, традиционно, содержит примеры. Например, на этом слайде приводится восемь примеров, ниже чего описаны их подробные решения. Как видим, среди этих примеров есть и очевидные. При решении каждого из них, автор показывает, что в первую очередь необходимо проверить подкоренное выражение. Если оно меньше нуля, то решить пример не имеет никакого смысла. Ведь квадратного корня от отрицательного числа не существует.


слайды 9-10 (примеры)
Так как подкоренные числа могут быть довольно большими, стоит знать, как их извлекать. Извлечение корня в этом случает довольно трудоемкий процесс. Для начала необходимо включить интуицию и подобрать несколько таких чисел, квадраты которых посчитать будет нетрудно. Например, числа 50 или 60 возвести в квадрат не составит никакого труда. Из примера видно, что подкоренное число находится между квадратами этих чисел. Перебирая квадраты всех возможных чисел, которые находятся между 50 и 60, можно найти искомое число. Таким образом, можно без помощи калькулятора найти арифметический корень из достаточно больших чисел.


слайды 11-12 (пример)
Далее приводится задача о нахождении гипотенузы некоторого прямоугольного треугольника. Из условия видим, что катеты уже заданы. По теореме Пифагора можно найти неизвестную сторону. Суть теоремы Пифагора заключается в том, что если треугольник прямоугольный, то квадрат гипотенузы этого треугольника равен сумме квадратов катетов этого же треугольника. Следовательно, при решении этого уравнения школьники столкнуться с арифметическим корнем. Другим способом записать ответ будет невозможно. На примере этой задачи можно показать практическое применение извлечения корня квадратного.
Где еще может применяться корень квадратный? Об этом говориться на следующем слайде. Здесь приведено квадратное уравнение. Для решения простых квадратных уравнений, то есть, для нахождения их корней, необходимо знать формулу дискриминанта, которая необходима для нахождения, непосредственно, корней. Подробное решение приведено ниже. Вот еще один пример применения арифметического корня, в этом случае, уже в алгебре.

слайд 13 (пример)
Далее приводится задача о нахождении гипотенузы некоторого прямоугольного треугольника. Из условия видим, что катеты уже заданы. По теореме Пифагора можно найти неизвестную сторону. Суть теоремы Пифагора заключается в том, что если треугольник прямоугольный, то квадрат гипотенузы этого треугольника равен сумме квадратов катетов этого же треугольника. Следовательно, при решении этого уравнения школьники столкнуться с арифметическим корнем. Другим способом записать ответ будет невозможно. На примере этой задачи можно показать практическое применение извлечения корня квадратного.
Где еще может применяться корень квадратный? Об этом говориться на следующем слайде. Здесь приведено квадратное уравнение. Для решения простых квадратных уравнений, то есть, для нахождения их корней, необходимо знать формулу дискриминанта, которая необходима для нахождения, непосредственно, корней. Подробное решение приведено ниже. Вот еще один пример приРаз существует квадратный корень, то становится очевидным факт существования корня кубического. Как она алгебраически записывается, демонстрирует последний слайд этой презентации. Также приводятся примеры корня 4й степени, 5й. Также приводится общая запись корня n-ой степени.
Данная тема является очень важной и, одновременно, не очень понятной на первый взгляд. Нужно как можно подробно и понятно объяснить школьникам арифметический корень квадрантный. Каждый школьник в этом возрасте должен научиться работать с ним, извлекать квадратный (или энный) корень, ведь при решении различных алгебраических или геометрических задач не обойтись без них. Даже в физике будут встречаться формулы, содержащие корни квадратных. Если есть возможность продемонстрировать параллельно объяснениям темы во время урока подобные мультимедийные файлы, то школьники смогут лучше воспринимать и запоминать информацию.менения арифметического корня, в этом случае, уже в алгебре.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7767 |
| Номер материала | 276 |