
Урок "Иррациональные числа"

Краткое описание документа:
Вы уже знаете, что числа бывают - натуральные, - целые и - рациональные. Числа, которые мы привыкли использовать, называются рациональными. Это можно легко отметить на примере рассмотрение треугольника. Пусть катеты будут равны 2 см и 3 см, тогда длинна гипотенузы, исходя из теоремы Пифагора, будет равна 22 + 32 = с. В данном примере с = √13 см, а √12,а это не является рациональным числом. Возьмем, к примеру, уравнение x2 = 3, корни которого также не будут рациональными числами: √3 и -√3. Так что же тогда мы можем считать не рациональным числами? На этот вопрос ищите ответ в видеоуроке.
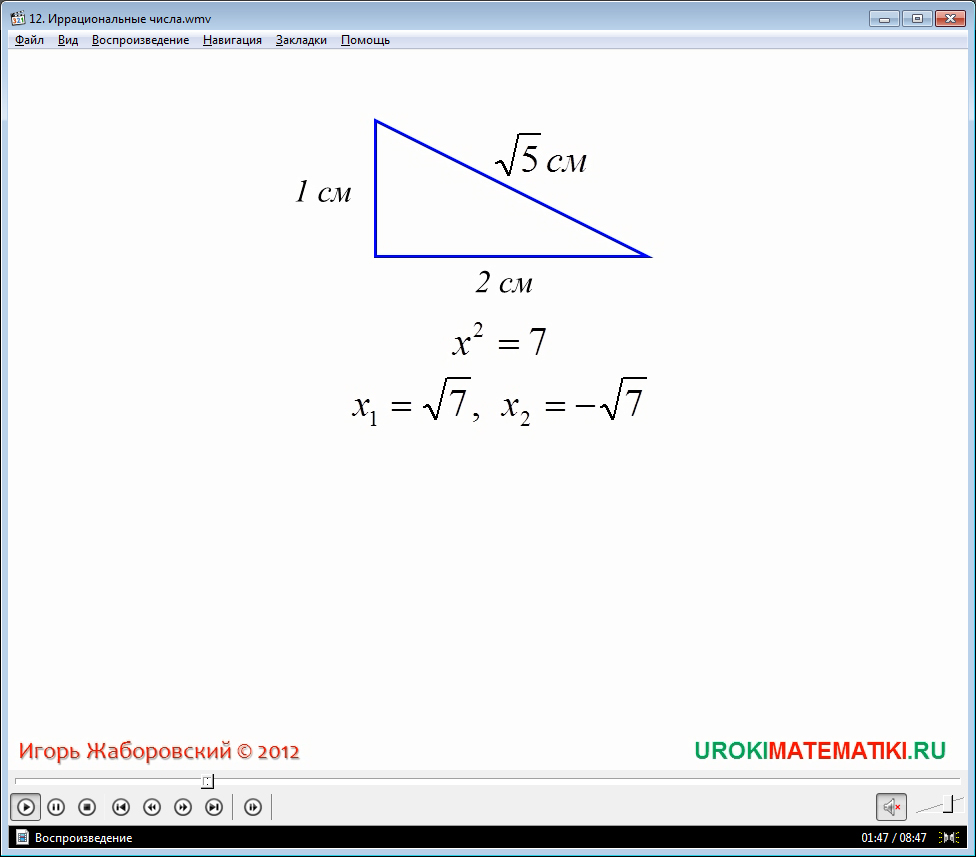
Во-первых, следует отметить, что такое понятие в математической терминологии, как «нерационально число», не принято использовать, ему на замену употребляют термин «иррациональное число». История терминов «рационально число», «иррациональное число» очень давняя и зародилась она от слова ratio, что в переводе с латинского означает «разум».
Приступим к рассмотрению иррационального числа, которые мы уже упоминали -√13. Это число находится в промежутке между числами 3 и 4. Прибегнув к точности, отметим, что √13 находится в промежутке 3,6055 < √13 < 3,6057. И это не предел, границы можно отметить и до пятого, шестого знака и далее. Известно, что √13 приблизительно равен 3,6056, но это значение неточное, и если считать, что для числа √13 будут выписаны последующие десятичные знаки, то имеет место запись √13 приблизительно равен 0,6056 …. Это число является бесконечной десятичной дробью. В предыдущих видеоуроках вы познакомились с бесконечными десятичными дробями, но они выражались при помощи рациональных чисел и были периодическими. А вот число √13 - это бесконечная десятичная непериодическая дробь. Такие числа встречаются не только во время извлечения корня, но и во многих других случаях.
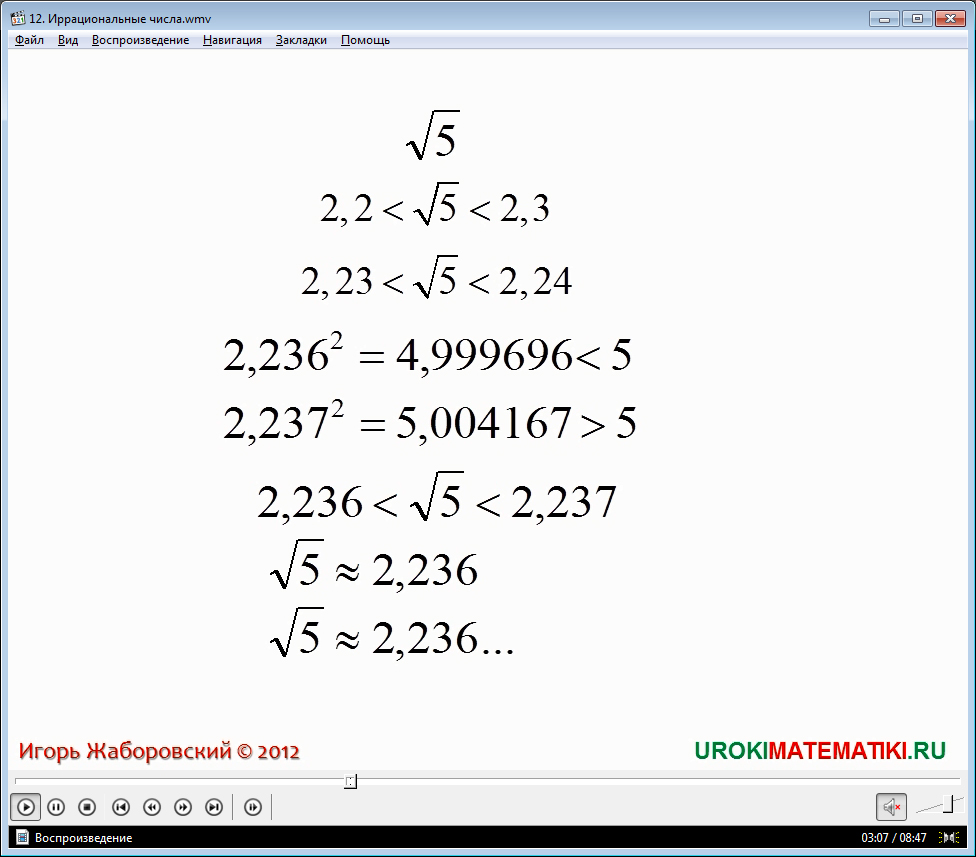
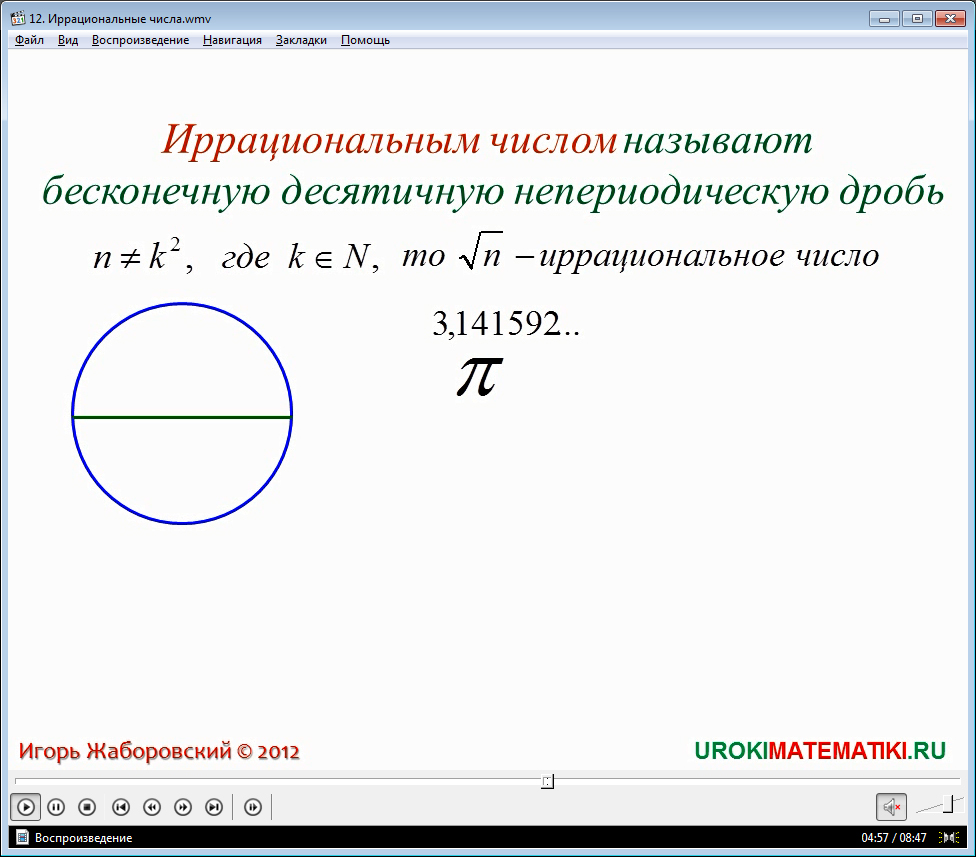
Иррациональное число – это бесконечная непериодическая дробь.
Рассмотрим пример. Разделив длину окружности на её диаметр, получим иррациональное число 3,141595 …. И это неоспоримый факт, который был установлен еще далеко до нашей эры великим философом и математическим учёным Архимедом. Специально для этого числа в математике существует обозначение – Пи. Исходя из логических соображений, любая арифметическая операция над рациональными числами в результате приводит к рациональному числу. Интересно, как обстоят дела с иррациональными числами. На самом деле, дать определенный ответ невозможно. Давайте рассмотрим это на примере: √13 – иррациональное число, √13 * √13 = 13 и это уже рациональное число, то есть произведение двух иррациональных чисел – рациональное число.
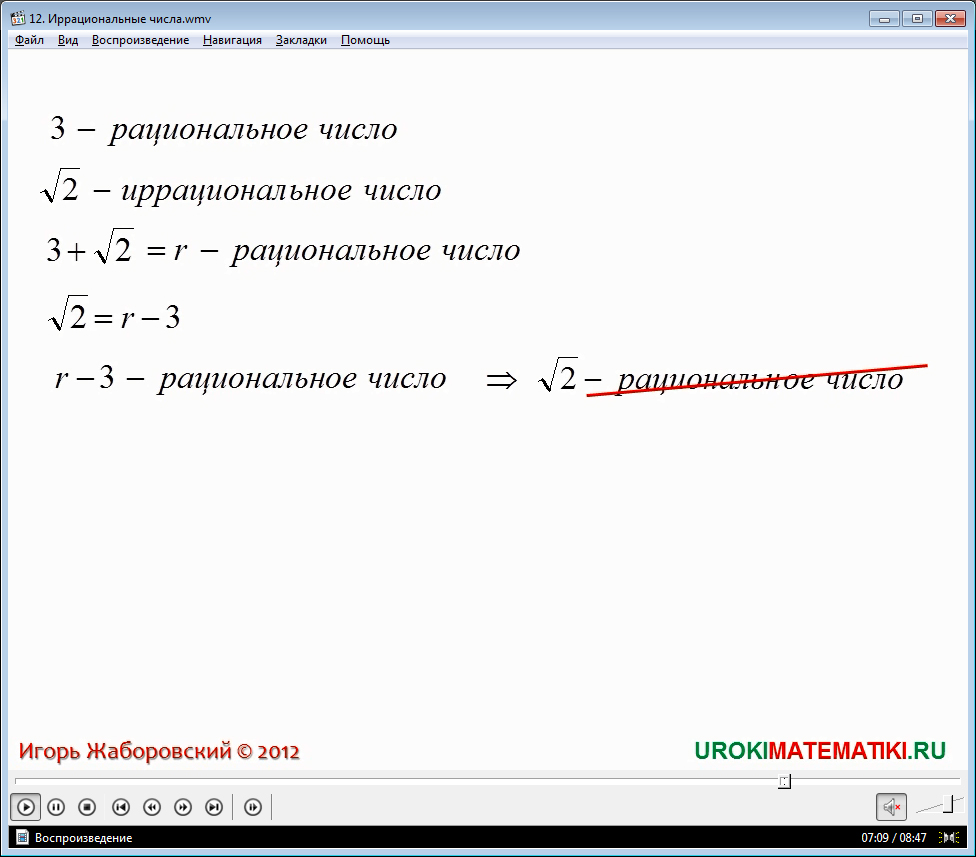
Другой пример. Возьмем два иррациональных числа √13 и √7 - иррациональные числа, их произведение √91- иррациональное число. То есть при различных математических операциях в результате мы можем получить как рациональное, так и иррациональное число. С аналогичными примерами и доказательственным методом от противного вы ознакомитесь при просмотре видеоурока.
Подведем небольшой итог:
- При выполнении любого арифметического действия с рациональными числами (исключая деление на 0) в результате вы получите рациональное число.
- Арифметическая операция над иррациональными числами может дать в результате как иррациональное, так и рациональное число.
- В случае, если в арифметической операции задействовано иррациональное и рациональное число, в итоге вы получите иррационально число.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 11534 |
| Номер материала | 536 |