
Презентация по математике Богомягковой Е. (10 "А" класс) на тему "Задания №8 из ЕГЭ (геометрия)"









Описание презентации по отдельным слайдам:
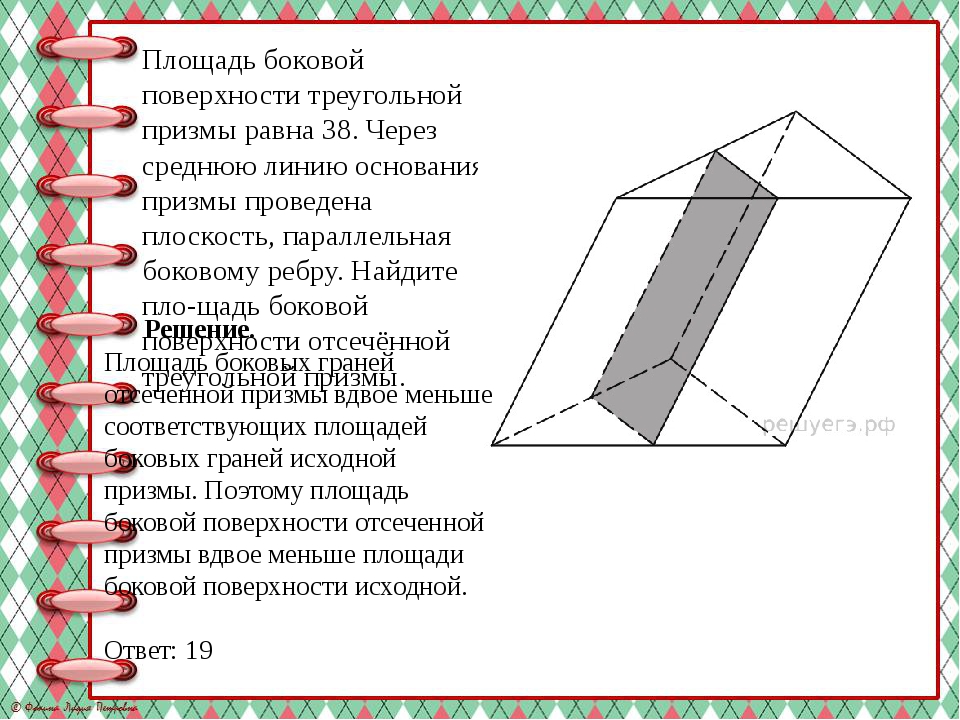
Площадь боковой поверхности треугольной призмы равна 38. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите пло-щадь боковой поверхности отсечённой треугольной призмы. Решение. Площадь боковых граней отсеченной призмы вдвое меньше соответствующих площадей боковых граней исходной призмы. Поэтому площадь боковой поверхности отсеченной призмы вдвое меньше площади боковой поверхности исходной. Ответ: 19
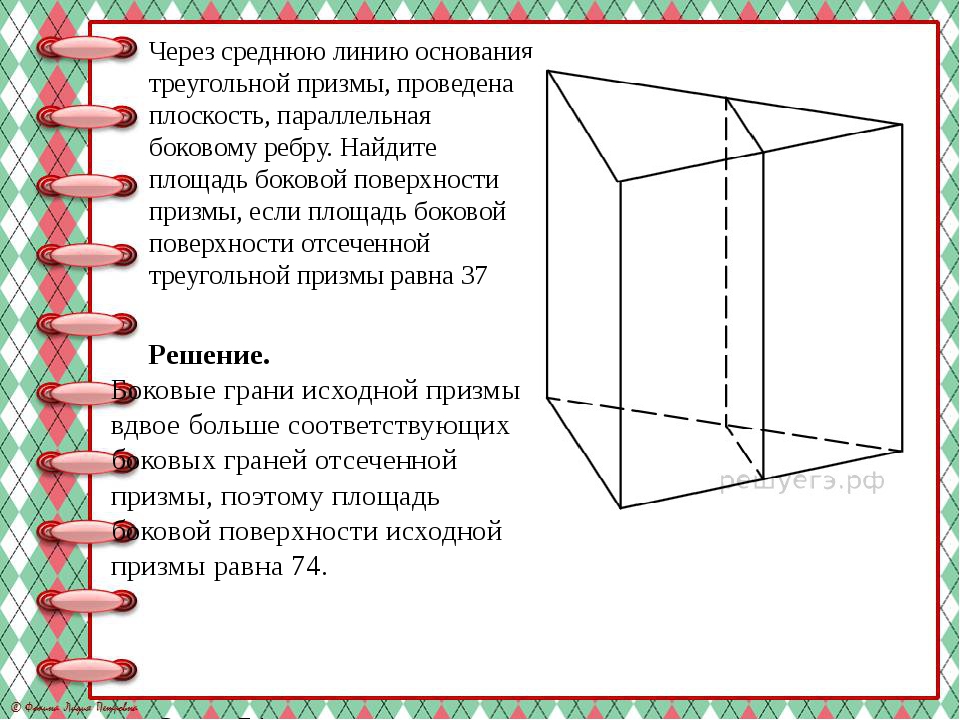
Через среднюю линию основания треугольной призмы, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности призмы, если площадь боковой поверхности отсеченной треугольной призмы равна 37 Решение. Боковые грани исходной призмы вдвое больше соответствующих боковых граней отсеченной призмы, поэтому площадь боковой поверхности исходной призмы равна 74. Ответ:74
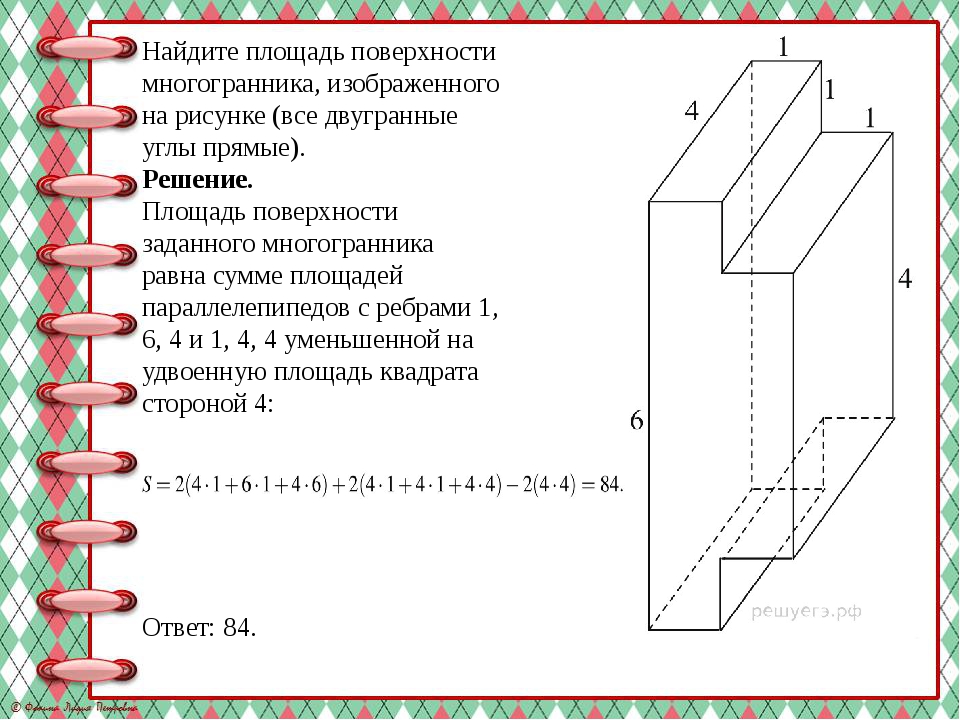
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Решение. Площадь поверхности заданного многогранника равна сумме площадей параллелепипедов с ребрами 1, 6, 4 и 1, 4, 4 уменьшенной на удвоенную площадь квадрата стороной 4: Ответ: 84.
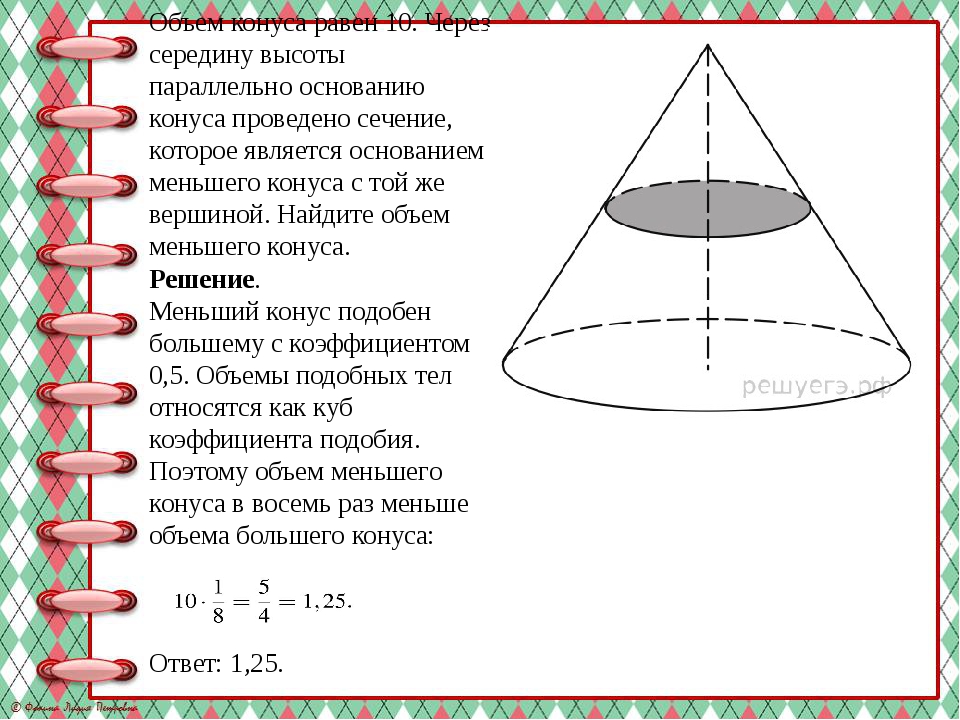
Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Решение. Меньший конус подобен большему с коэффициентом 0,5. Объемы подобных тел относятся как куб коэффициента подобия. Поэтому объем меньшего конуса в восемь раз меньше объема большего конуса: Ответ: 1,25.
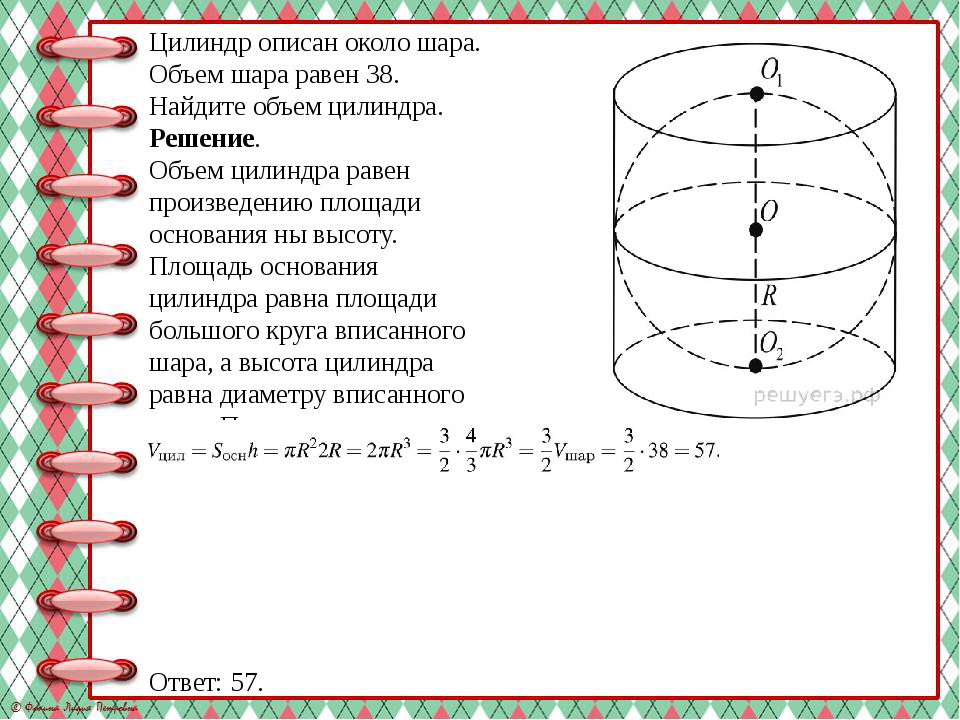
Цилиндр описан около шара. Объем шара равен 38. Найдите объем цилиндра. Решение. Объем цилиндра равен произведению площади основания ны высоту. Площадь основания цилиндра равна площади большого круга вписанного шара, а высота цилиндра равна диаметру вписанного шара. Поэтому Ответ: 57.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Решение. Площадь поверхности тела равна сумме поверхностей трех составляющих его параллелепипедов с измерениями 2, 4, 6; 1, 6, 2 и 2, 2, 2: Ответ: 152.
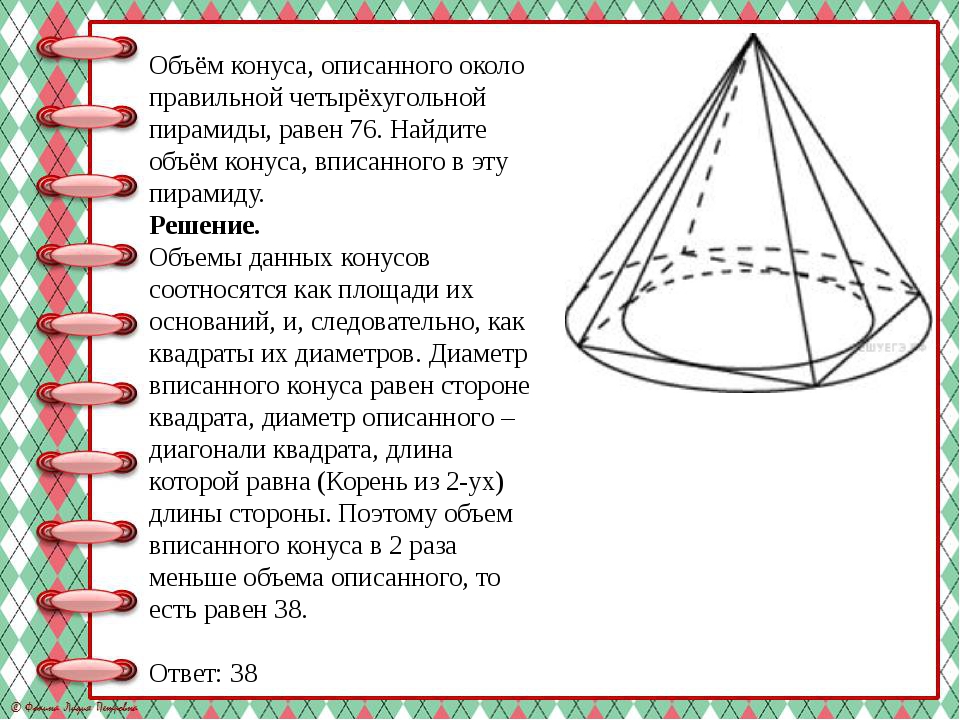
Объём конуса, описанного около правильной четырёхугольной пирамиды, равен 76. Найдите объём конуса, вписанного в эту пирамиду. Решение. Объемы данных конусов соотносятся как площади их оснований, и, следовательно, как квадраты их диаметров. Диаметр вписанного конуса равен стороне квадрата, диаметр описанного – диагонали квадрата, длина которой равна (Корень из 2-ух) длины стороны. Поэтому объем вписанного конуса в 2 раза меньше объема описанного, то есть равен 38. Ответ: 38
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов. Решение. Крест состоит из 7 одинаковых кубов, поэтому его объем в 7 раз больше объема одного куба. Ответ: 7.
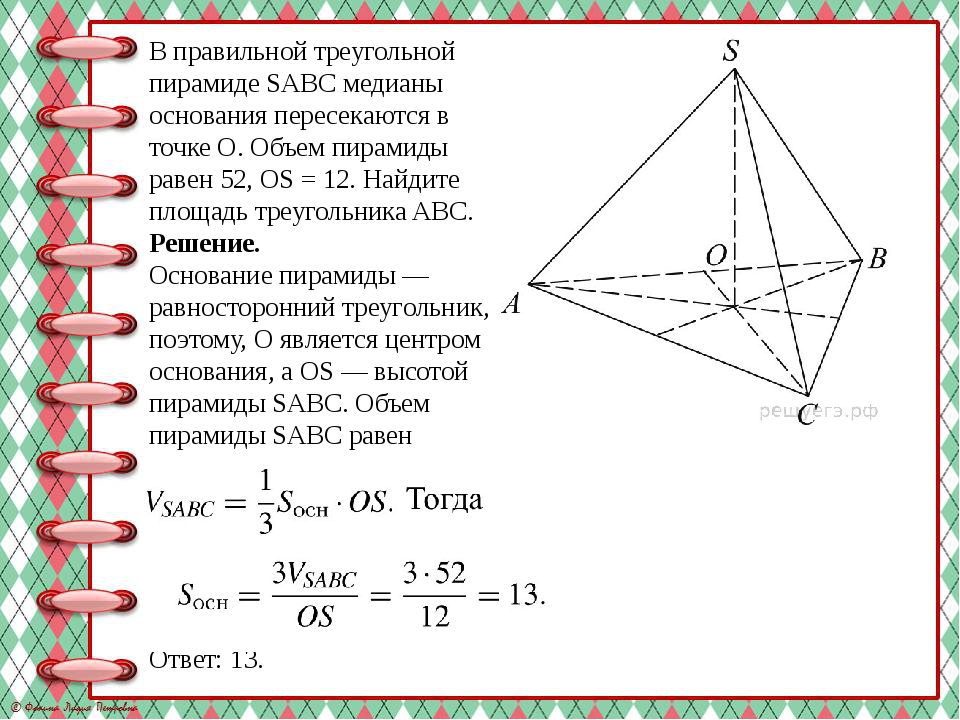
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке O. Объем пирамиды равен 52, OS = 12. Найдите площадь треугольника ABC. Решение. Основание пирамиды — равносторонний треугольник, поэтому, O является центром основания, а OS — высотой пирамиды SABC. Объем пирамиды SABC равен Ответ: 13.
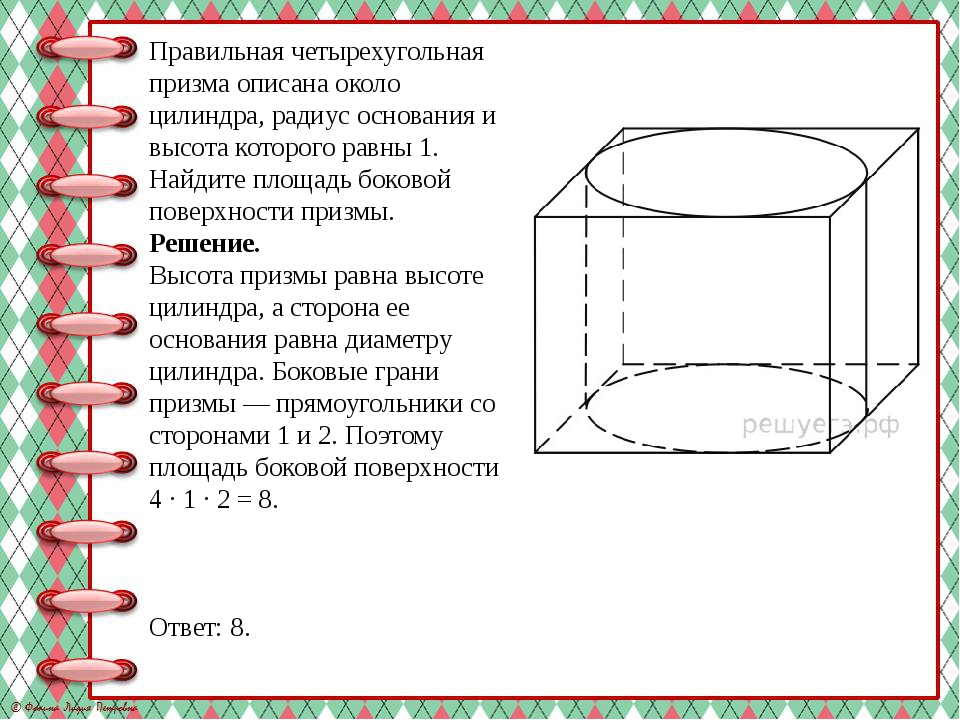
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Решение. Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8. Ответ: 8.
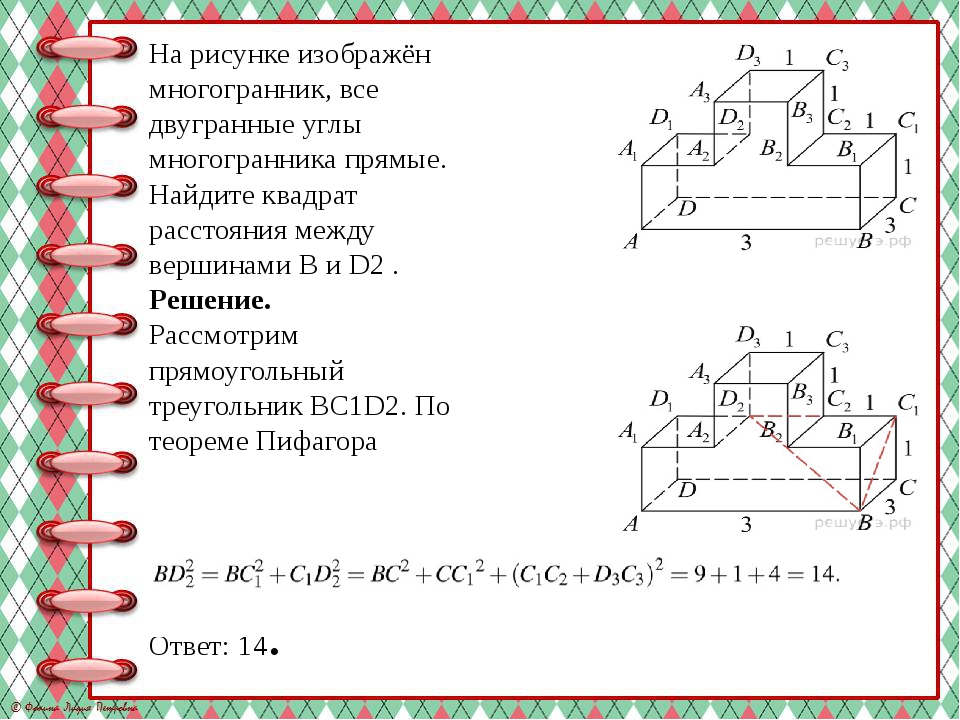
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами B и D2 . Решение. Рассмотрим прямоугольный треугольник BC1D2. По теореме Пифагора Ответ: 14.
Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба? Решение. Объемы подобных тел относятся как куб коэффициента подобия, поэтому один из кубов в 2 раза больше другого. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия, поэтому их отношение равно 4. Ответ: 4.
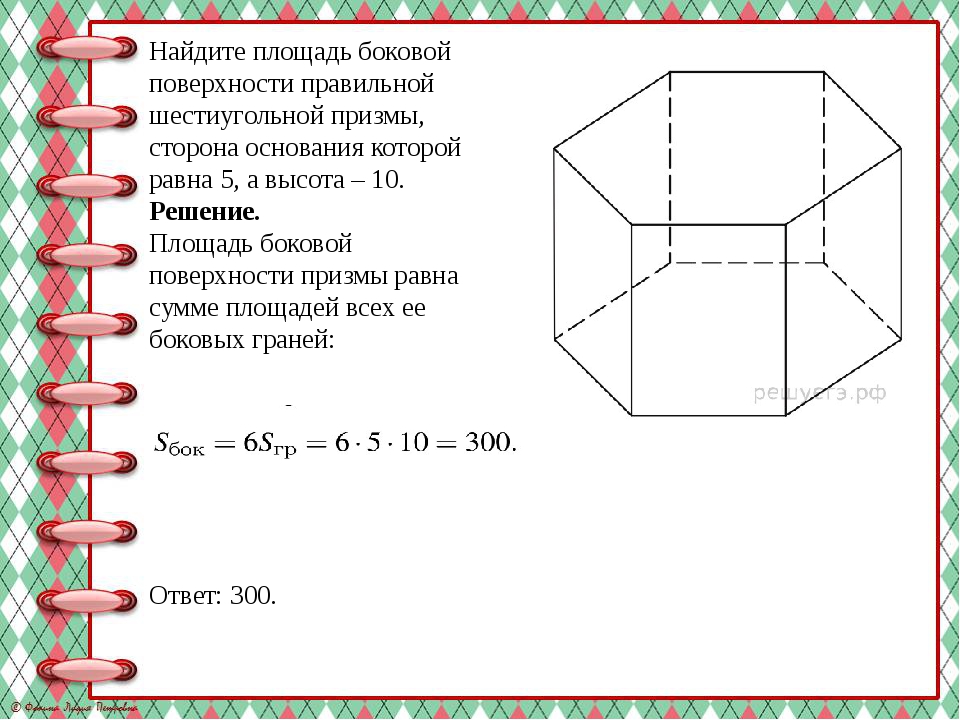
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10. Решение. Площадь боковой поверхности призмы равна сумме площадей всех ее боковых граней: Ответ: 300.
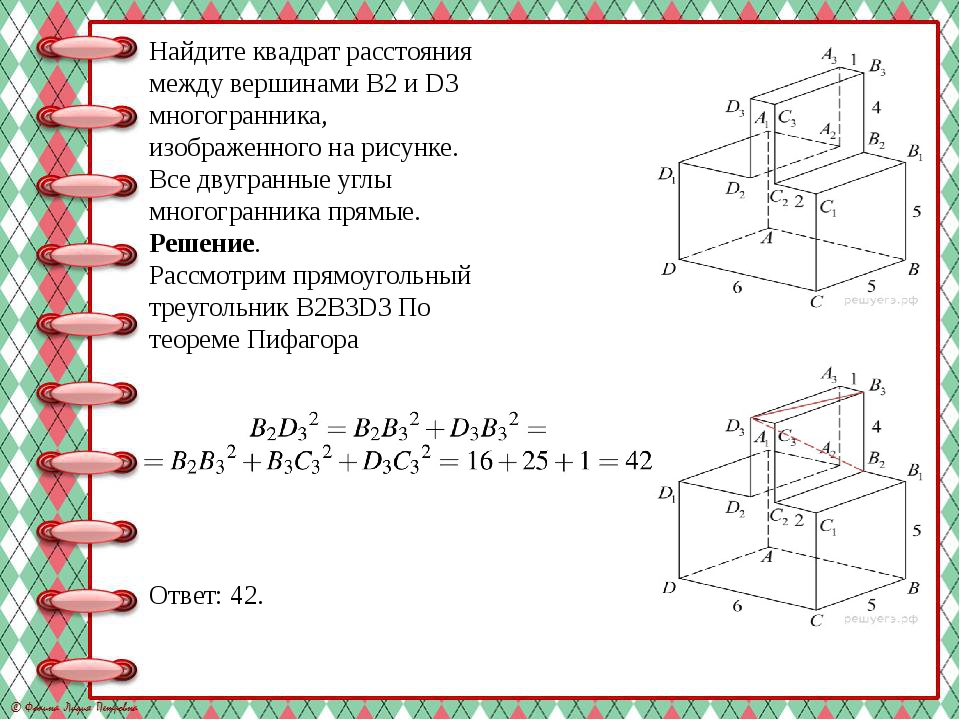
Найдите квадрат расстояния между вершинами B2 и D3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Решение. Рассмотрим прямоугольный треугольник B2B3D3 По теореме Пифагора Ответ: 42.
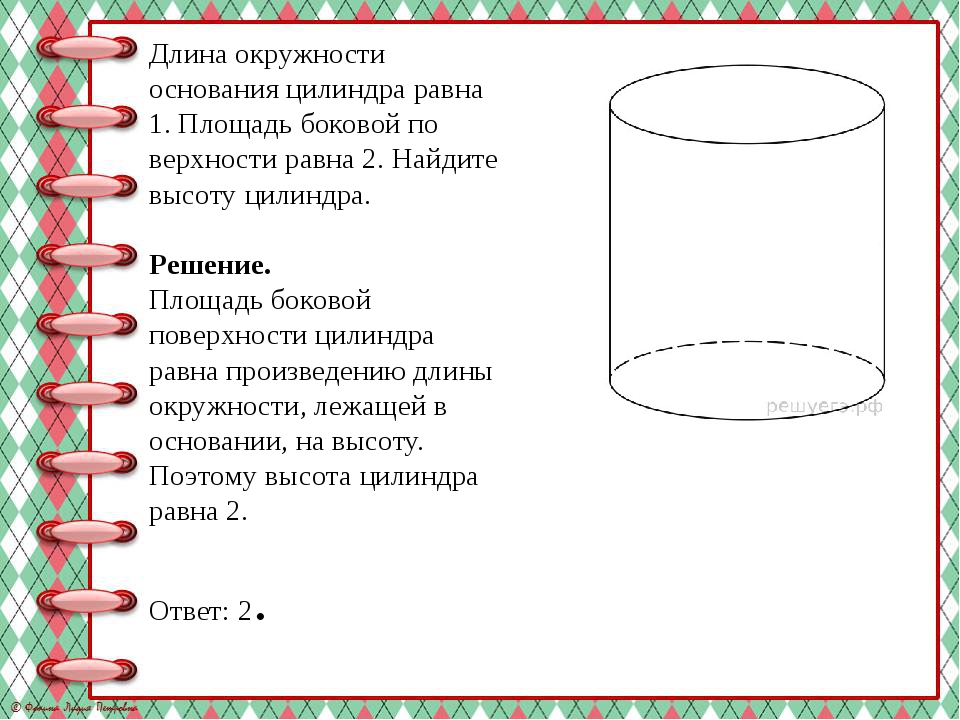
Длина окружности основания цилиндра равна 1. Площадь боковой по верхности равна 2. Найдите высоту цилиндра. Решение. Площадь боковой поверхности цилиндра равна произведению длины окружности, лежащей в основании, на высоту. Поэтому высота цилиндра равна 2. Ответ: 2.
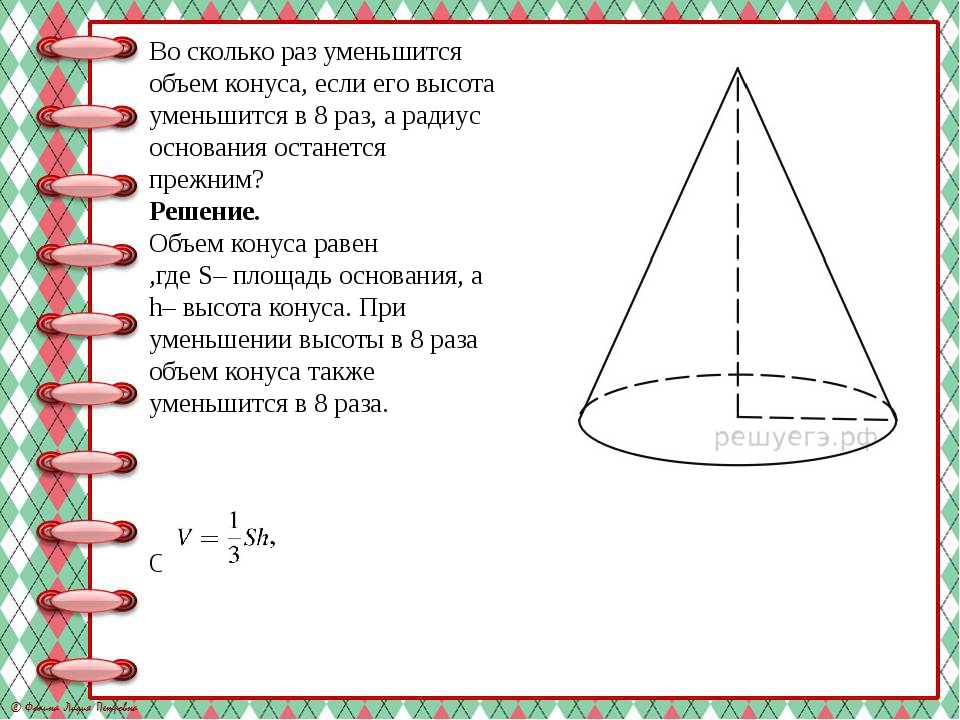
Во сколько раз уменьшится объем конуса, если его высота уменьшится в 8 раз, а радиус основания останется прежним? Решение. Объем конуса равен ,где S– площадь основания, а h– высота конуса. При уменьшении высоты в 8 раза объем конуса также уменьшится в 8 раза. Ответ: 8
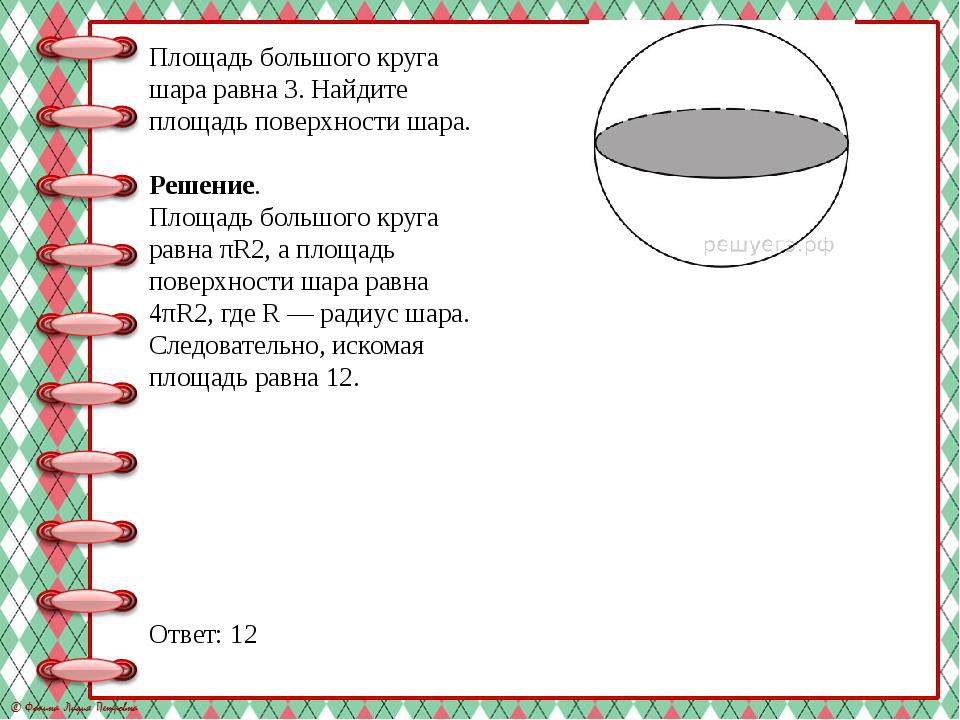
Площадь большого круга шара равна 3. Найдите площадь поверхности шара. Решение. Площадь большого круга равна πR2, а площадь поверхности шара равна 4πR2, где R — радиус шара. Следовательно, искомая площадь равна 12. Ответ: 12
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые). Решение.Площадь поверхности многогранника — площадь параллелепипеда со сторонами 5, 3, 2 за вычетом двух "боковых" площадей прямоугольников со сторонами 2 и 1: S=2(5*3+3*2+5*2)-2*2*1=58 Ответ: 58.
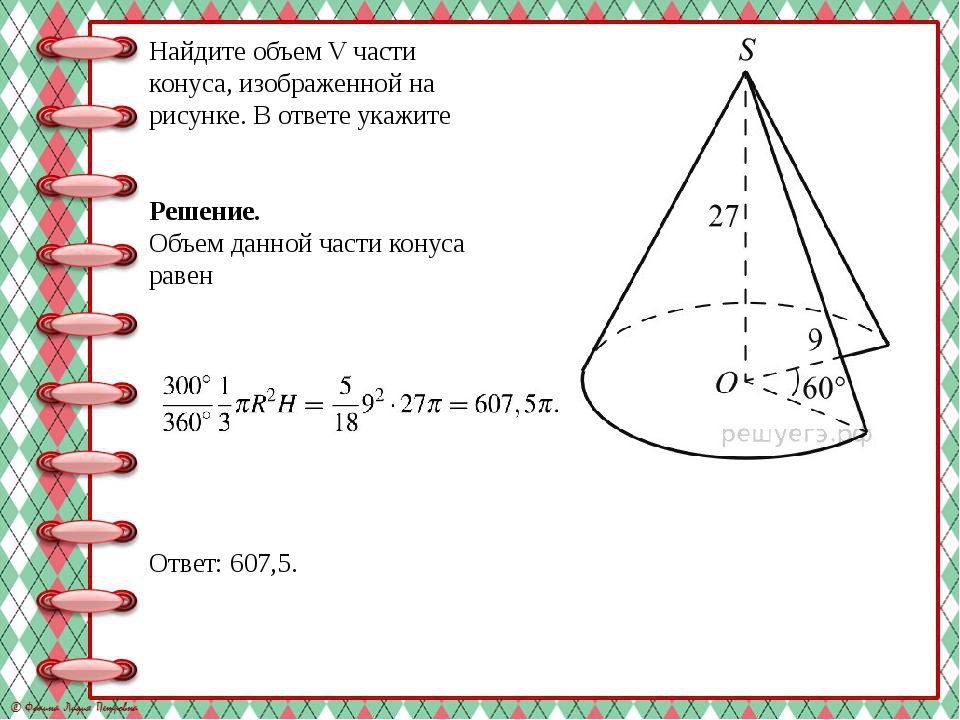
Найдите объем V части конуса, изображенной на рисунке. В ответе укажите Решение. Объем данной части конуса равен Ответ: 607,5.
Радиусы двух шаров равны 21 и 72. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров. Решение. Ответ: 75.
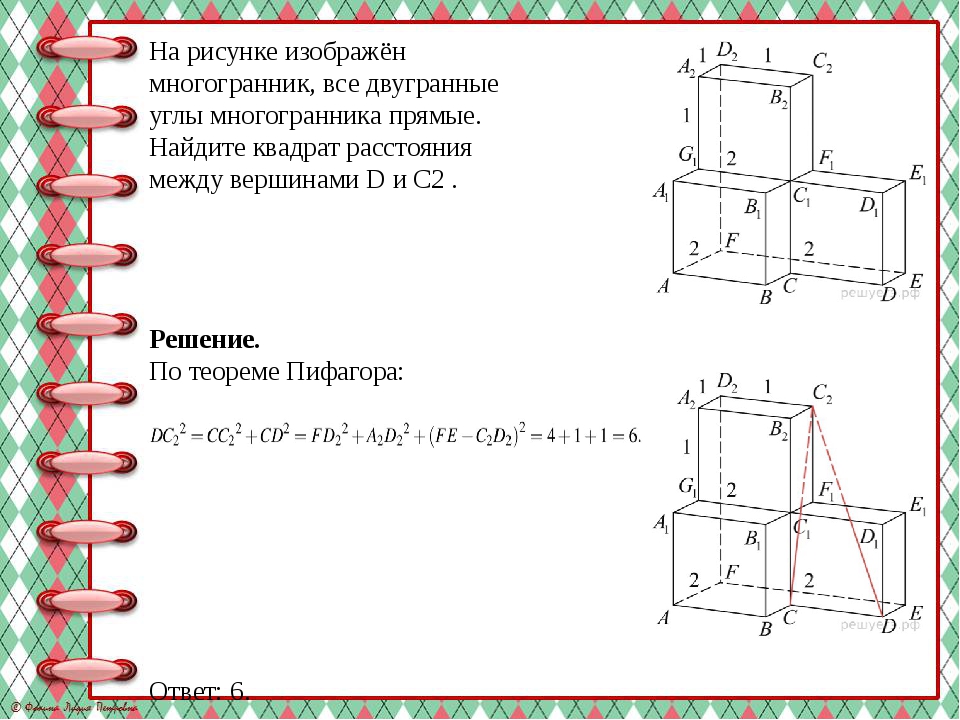
На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите квадрат расстояния между вершинами D и C2 . Решение. По теореме Пифагора: Ответ: 6.
В куб вписан шар радиуса 3. Найдите объем куба. Решение. Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем: Ответ: 216.
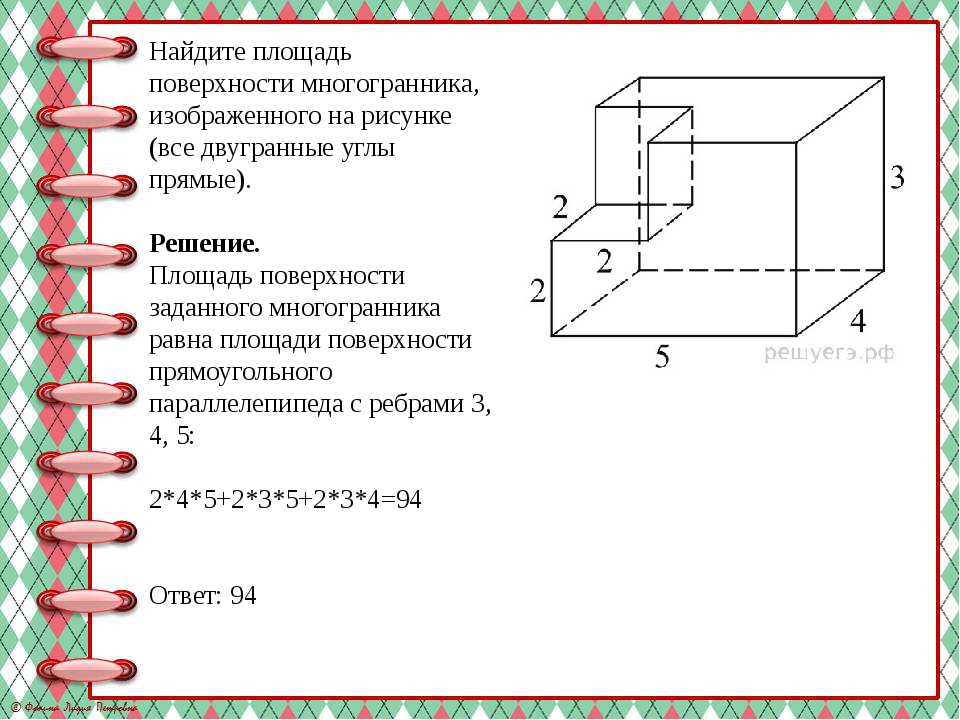
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Решение. Площадь поверхности заданного многогранника равна площади поверхности прямоугольного параллелепипеда с ребрами 3, 4, 5: 2*4*5+2*3*5+2*3*4=94 Ответ: 94
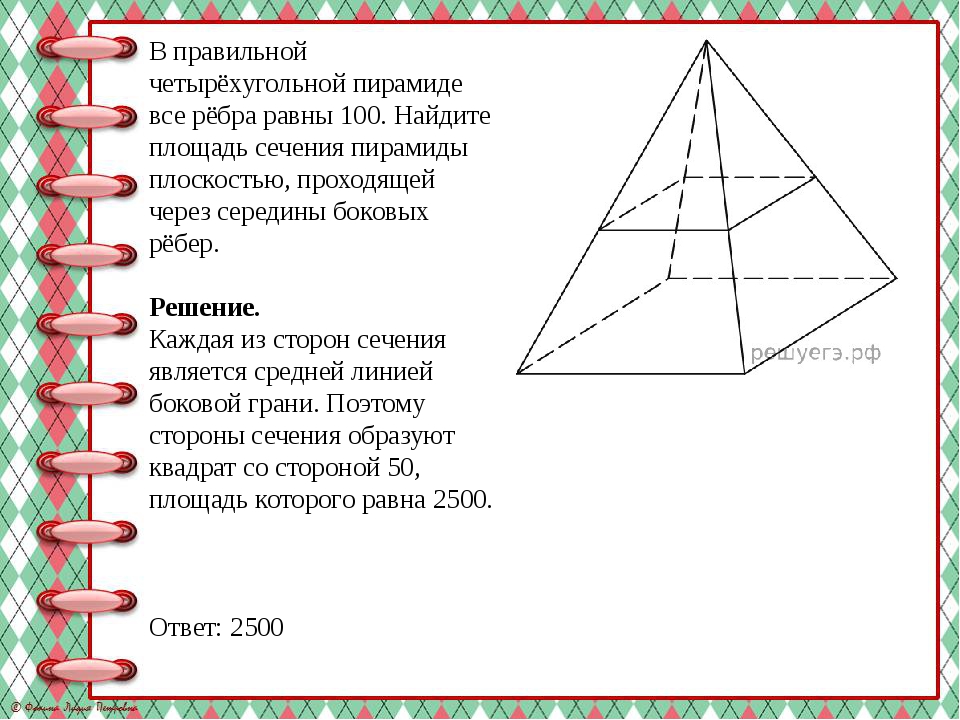
В правильной четырёхугольной пирамиде все рёбра равны 100. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер. Решение. Каждая из сторон сечения является средней линией боковой грани. Поэтому стороны сечения образуют квадрат со стороной 50, площадь которого равна 2500. Ответ: 2500
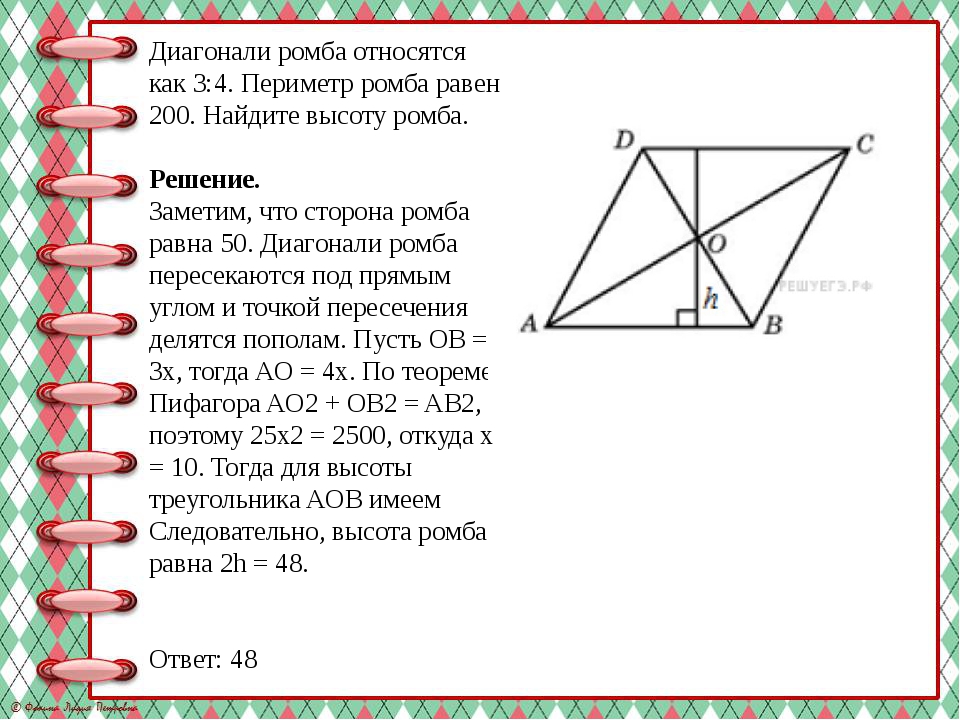
Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба. Решение. Заметим, что сторона ромба равна 50. Диагонали ромба пересекаются под прямым углом и точкой пересечения делятся пополам. Пусть OB = 3x, тогда AO = 4x. По теореме Пифагора AO2 + OB2 = AB2, поэтому 25x2 = 2500, откуда x = 10. Тогда для высоты треугольника AOB имеем Следовательно, высота ромба равна 2h = 48. Ответ: 48

| Автор | |
|---|---|
| Дата добавления | 03.06.2019 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 4145 |
| Номер материала | 6246 |