
Презентация "Построение треугольника по трём элементам"

Краткое описание документа:
На сегодняшнем уроке мы более подробно познакомимся с задачами на построение. Построение треугольника по трём элементам и задачи на построение в целом – это объёмный класс. С простейшими из них мы сталкивались при работе с теоремами, а теперь стоит применить все наработанные теоретические знания на решение типичных задач.

слайды 1-2 (Тема презентации "Построение треугольника по трём элементам", пример)
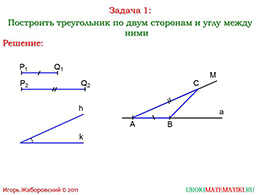
Итак, в условие нашей задаче есть три элемента: две стороны и угол между этими сторонами. Мы знаем признак равенства треугольника по двум сторонам и углу. Значит, когда две стороны и угол одного треугольника соответственно идентичны двум сторонам и углу другого треугольника, то такие треугольники равные. То есть, может быть бесчисленное множество таких треугольников на доске в разных углах, но по факту это будет один и тот же треугольник. Таким образом, две стороны и угол однозначно задают треугольник, который в конечном итоге можно перемещать по плоскости. Так вот такой треугольник нам и нужно построить.
Нарисуем треугольник «АВС», который нам нужно будет построить. Используем достаточно стандартные обозначения.
Получается, нам дан некоторый отрезок «P1Q1». Второй отрезок «P2Q2», оба отрезка являются искомыми треугольника. Также дан угол «hk». Величина угла задана, но не определена. Однако мы помним, что она не может быть выше ста восьмидесяти градусов.
Возьмём прямую и на ней отложим отрезок «P2Q2», длину которого мы можем измерить с помощью циркуля. Мы знаем, что на прямой мы можем отложить отрезок от заданной точки, зная его длину. Что мы, собственно и делаем. Далее от заданного луча измеряем заданный угол и из нашей точки продолжаем луч под определённым углом. Угол можно измерять с помощью транспортира. На новом луче откладываем отрезок «P1Q1». Конечные точки на лучах необходимо соединить, и получим треугольник. Является ли треугольник искомым? Да, потому что использованы все необходимые данные.
слайды 3-4 (примеры)
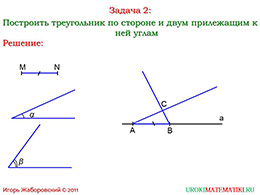
Эта задача также соответствует признаку равенства треугольников, который говорит о том, что треугольники равны, если сторона и два прилежащих к ней угла идентичны. Конкретно данная задача заключается в следующем. Также нарисуем треугольник, который нам следует построить и обозначим его «АВС». Нам дан отрезок, длиною «MN», угол «бета» и «альфа».
На произвольной прямой откладываем точку «А». От данной точки откладываем необходимый отрезок, предварительно измерив его длину циркулем. Далее из точки «А» откладываем угол «альфа», а из вершины «В» откладываем необходимый угол «бета». Точка пересечения тих лучей будет являться третей вершиной заданного треугольника. Утверждаем, что треугольник «АВС» искомый. Почему? Потому что сторона «АВ» равна исходной стороне «MN», а заданные углы мы находим при основании полученной фигуры. Строить треугольники можно в разных плоскостях, они в любом случае будут искомыми.
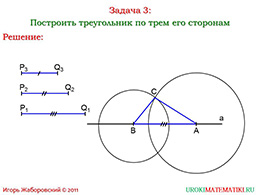
Для закрепления третий пример необходимо дать учащимся на самостоятельный разбор, который потом проанализирует преподавать вместе с одним из учащихся. Изначально даны некоторые отрезки длиной «P1Q1», «P2Q2», «P3Q3». Мы видим, что отрезки различной длины, то есть никакие из них не равны, поэтому у нас получится произвольный треугольник. Для решения задачи вновь понадобиться линейка и циркуль.
Построим некоторую прямую «а», на которой поставим точку «В». От этой точки отложим отрезок длиною «P1Q1», так как он самый большой. Далее циркулем измеряем отрезок «P3Q3» и рисуем окружность с центром в точке «В». После этого повторяем действие, но уже в точке «А» рисуем окружность с радиусом «P2Q2». На точке пересечения окружностей находится третья вершина нашего треугольника. Этих точек будет две, но не важно, в какой плоскости вы нарисуете треугольник, потому что в любом случае он будет искомым.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 8763 |
| Номер материала | 265 |