
Презентация "Расстояние от точки до прямой. Расстояние между параллельными прямыми"

Краткое описание документа:
В данном уроке мы подробнее остановимся на расстоянии от точки до некоторой прямой, а также проанализируем расстояние между двумя параллельными прямыми. Итак, говорим о расстоянии между различными фигурами. Мы знаем, что при наличии точек «А» и «В» расстоянием между ними будет являться длина отрезка «АВ». Данные точки являются элементарными геометрическими фигурами. Длина отрезка является самым коротким путём, который идёт из одной точки в другую. Более длинным расстояние может стать, если путь будет идти ломано через какую-то другую точку или по дуге.

слайды 1-2 (Тема презентации "Расстояние от точки до прямой. Расстояние между параллельными прямыми", пример)
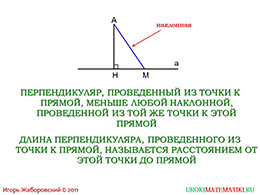
Что тогда мы можем назвать расстоянием от точки «А» до прямой «а»? Вспомним, что ключевым словом является «минимизация» расстояния между двумя геометрическими фигурами. Мы можем провести отрезки на различные части прямой, но что будет самым коротким путём для того, чтобы соединить некую точку с некой прямой? Ответ прост: используем перпендикуляр.
Опустим перпендикуляр из точки «А» на прямую «а». Теперь необходимо доказать, что перпендикуляр «АН» короче любой наклонной. Рассмотрим треугольник «АНМ» и увидим, что катетом является длина перпендикуляра «АН», а наклонная «АМ» выступает гипотенузой. Нам известно, что гипотенуза длиннее любого катета, потому что она лежит напротив самого большого угла – прямого угла «Н», который равен девяносто градусов. Поэтому вполне естественно назвать ближайшее расстояние от точки «А» до прямой «а» - тот перпендикуляр, который мы к прямой провели.
То есть, исходя из главного принципа минимизации расстояния, мы определили, что расстоянием от точки до прямой является длина перпендикуляра.
Естественно нам придётся находить длину этого перпендикуляра в разных задачах, причём достаточно строго. Однако, зная свойства и признаки прямоугольных треугольников, это не составит труда.

слайды 3-4 (пример, теорема)
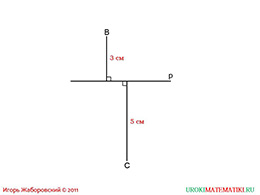
Мы уже знаем, что является кратчайшим расстоянием между двумя точками (отрезок), а также кратчайшим расстоянием от точки до прямой (перпендикуляр). Обратим внимание на пример, где дано два перпендикуляра из точек «В» и «С» на прямую «Р». Эти точки лежат в разных полуплоскостях, но являются кратчайшим расстоянием до прямой. Попробуем доказать равенство или неравенство треугольников «ВОМ» и «СМО».
Итак, оба треугольника прямоугольные, потому что мы имеем дело с перпендикулярами, соответственно углы «ВОМ» и «СМО» равны девяносто градусов. Более того, у нас есть общая сторона «МО». Получается, что у нас есть равенство прямого угла и катета. Если вспомним все признаки прямоугольного треугольника, то поймём, что необходимо дополнительно знать, что прилежащие острые углы равные или же вторые катеты. К сожалению, равенство углов мы доказать не можем, но мы видим неравенство вторых катетов, поэтому треугольники «ВОМ» и «СМО» не равны.
Теперь есть две прямые «а» и «b», причём они параллельны между собой. Что мы можем назвать расстоянием от одной прямой к другой? Мы уже знаем, что такое расстояние между двумя точками, что такое расстояние между точкой и прямой и теперь переходим к более сложным геометрическим фигурам.
Возьмём произвольную точку «А» на прямой «а» и опустим перпендикуляр «АВ» на прямую «b». Хотелось бы именно его назвать расстоянием между двумя прямыми. А что, если взять другую точку на прямой, например, точку «Х» на этой же прямой? Тогда опустим перпендикуляр на прямую «b» и также получим кротчайшее расстояние «ХУ». Разная ли будет длина у этих отрезков? Попробуем доказать, что, если «АВ» перпендикулярна «b», а «ХУ» перпендикулярна данной прямой, то они буду равны между собой. То есть, мы должны доказать равенство всех перпендикуляров в параллельных прямых, не обращая внимание на то, какую точку мы взяли.


слайды 5-6 (примеры)
Доказав предыдущее утверждение, мы и поймём, чем является расстояние между параллельными прямыми. Заметим, что если отрезок «АВ» перпендикулярен прямой «b», а прямые «а» и «b» параллельны, то отсюда следует, что «АВ» не только перпендикулярна прямой «b» по построению, но и перпендикулярна прямой «а». Идентично с отрезком «ХУ», который перпендикулярен обеим прямым. Соединим точки «А» и «У».
Теперь рассмотрим треугольник «АУВ» и треугольник «АУХ». Наша цель – доказать равенство «АВ» и «ХУ», которые спрятаны в наших треугольниках. То есть, доказав равенство треугольников, мы докажем равенство этих сторон. Именно такой приём часто помогает при решении геометрических задач.
Эти два треугольника прямоугольные, имеют общую сторону «АУ», которая выступает гипотенузой. В силу того, что прямые «а» и «b» параллельны, их накрест лежащие углы равны. Таким образом, треугольник «АУВ» равен треугольнику «АУХ» по гипотенузе и острому углу, а значит отрезки «АВ» и «ХУ» равны.
Вовсе не сложно доказать и обратную теорему, где расположение равноудалённых от одной прямой точек находится на параллельной прямой, если все эти точки в одной полуплоскости (обратим внимание на формулировку).
Итак, мы вспомнили, что такое расстояние между простейшими двумя фигурами: точками. Наименьшее расстояние – длина самого отрезка. Далее, мы ввели кротчайшее расстояние от точки до прямой, которое выступило перпендикуляром. Мы определили расстояние между параллельными прямыми, введя любую точку, опустив перпендикуляр. После ясности определений необходимо уметь находить все эти расстояния и, соответственно, строить их.
В задачах необходимо обращать внимание на малейшие детали: наличие точек в одной плоскости, равенство катетов и гипотенуз. В таком случае, зная свойства и признаки прямоугольных треугольников, можно будет быстро найти решение, и геометрия станет одним из любимых предметов для учащихся.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 8653 |
| Номер материала | 264 |