
Презентация "Преобразование выражений, содержащих операцию извлечения квадратного корня"

Краткое описание документа:
При преобразовании различных выражений, как простых, так и сложных, во время курса алгебры, школьники столкнуться с необходимостью извлекать квадратные корни. Именно этому посвящена данная презентация. Благодаря этому обучающему ресурсу понять эту тему будет проще, ведь в ней приводятся простые примеры.

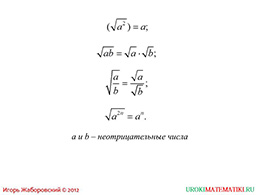
слайды 1-2 (Тема презентации "Преобразование выражений, содержащих операцию извлечения квадратного корня", пример)
На первом слайде приводятся четыре основных свойства, которые уже были изучены в предыдущих уроках. К этим свойствам относятся: извлечение корня от выражения, которое возведено в квадрат, свойства умножения и деления дробей и извлечение корня квадратного из степенного выражения. При этом, школьникам напоминается, что подкоренное выражение, ни в коем случае, не может являться отрицательным числом.


слайды 3-4 (примеры)
Сразу же после этого, автор предлагает перейти к практическим примерам. Первый пример состоит из двух аналогичных заданий. Школьникам приводятся выражения, которые необходимо упростить. Решения, разумеется, также приводятся. Прежде чем просмотреть решения, ученики могут попробовать самостоятельно решить эти примеры. Они могут просмотреть решение, чтобы проверить свои результаты.
Во втором примере, который приводится на этом же слайде сразу после первого примера, необходимо вынести из-под знака корня квадратного множитель. Зная свойства корней квадратных, выполнить эти действия, школьники смогут самостоятельно. Так что учителя могут не спешить с демонстрированием их решений.
Третий пример, который приводится на последующей странице презентации, предлагает выполнить обратный процесс, то есть необходимо внести под знак корня квадратного некоторые множители. Решения приводятся.


слайды 5-6 (примеры)
В четвертом примере необходимо выполнить действия, которые приводятся на странице. Для того, чтобы справиться с этим заданием, школьники должны вспомнить формулу разности квадратов и свойства квадратных корней. Очень полезно периодически ссылаться на изученный ранее материал, чтобы ученики его не забывали. В примере б) необходимо вспомнить формулу квадрата суммы.
Перейдем к следующему слайду. Здесь на примере приводится упрощение выражения. При упрощении используется изученный материал. Выполнив этот пример, материал закрепится в памяти учащихся.


слайды 7-8 (примеры)
В следующем примере необходимо избавиться от корней в знаменателе. Чтобы выполнить это задание школьники должны знать важное свойство дробей. Заключается оно в следующем: при умножении или делении на некоторое выражение и числитель, и знаменатель, значение дроби не измениться. При этом необходимо помнить, что в знаменателе не может быть ноль. Так же, как и в предыдущем примере, используются знания некоторых формул.


слайды 9-10 (пример)
Следующая страница содержит в себе текст. В ней говорится о том, в каких случаях говорят, что знаменатель содержит иррациональность и что означает «избавляться от иррациональности». Предыдущий слайд привел пример, в котором мы избавлялись от иррациональности в знаменателе, то есть от корней.
Также, на этом слайде говорится о том, что же является сопряженным выражением. Текст написан на таком уровне, чтобы школьники смогли воспринять информацию.
И последний заключающий слайд приводит решение примера, в котором рассматриваются все моменты, которые описывались в этой презентации. Выполняется упрощение выражения поэтапно и понятно. Ученики могут выполнить самостоятельно это задание, а потом сравнить ответы.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7322 |
| Номер материала | 282 |