
Урок "Функция y=√x, её свойства и график"

Краткое описание документа:
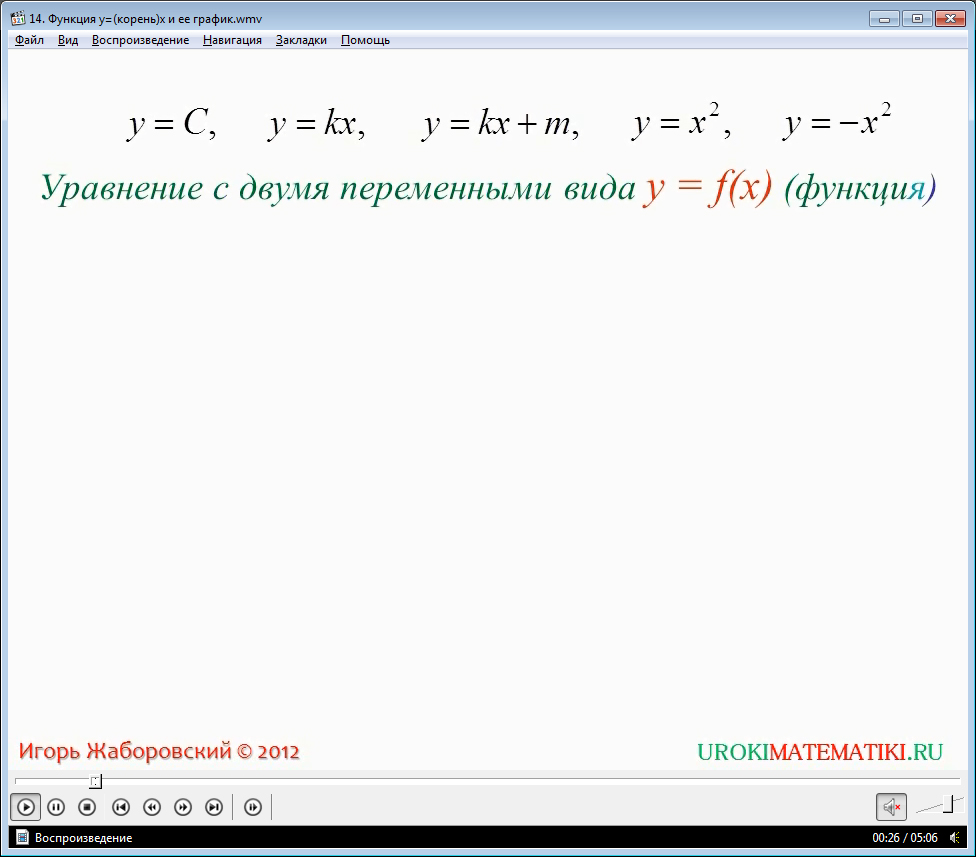
Ранее вы уже встречались с понятием функции и с некоторыми её разновидностями. Вспомним: функция – это удобная интерпретация записи зависимости зависимой переменной (у нас это y) от независимой переменной (в данном случае это x). Проще говоря, мы просто используем математическую запись того, как y зависит от x вот в таком виде – y = f(x)
Например:
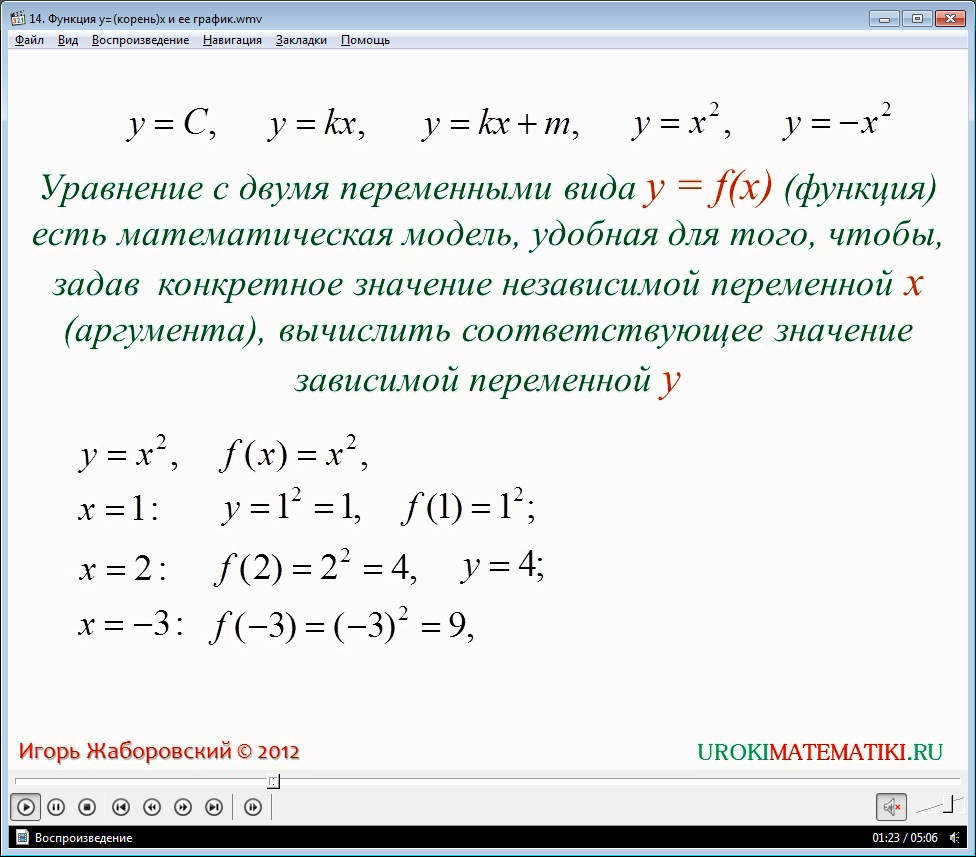
Если нам дана функция y = x3 или же f(x) = x3, то найти значение игрикаможно, подставляя различные значения икса.
Если x=0, то y = 03 = 0, или же f(0) = 03 = 0.
Так, изменяя аргумент функции (икс), мы получаем различные значения игрика:
если x=1, то y = 13 = 1 * 1 * 1 = 1, или же f(1) = 13 = 1.
если x=2, то y = 23 = 2 * 2 * 2 = 8, или же f(2) = 2 = 8.
если x=3 то y = 33 = 3 * 3 * 3 = 27, или же f(3) = 33 = 27.
и так далее.
Из встречавшихся вам ранее функций можно записать такие:
y = C, y = kx, y = kx + m y = x2, y = -x2
но, как вам уже известно, разнообразие всех возможных формул не ограничивается лишь описанными выше.
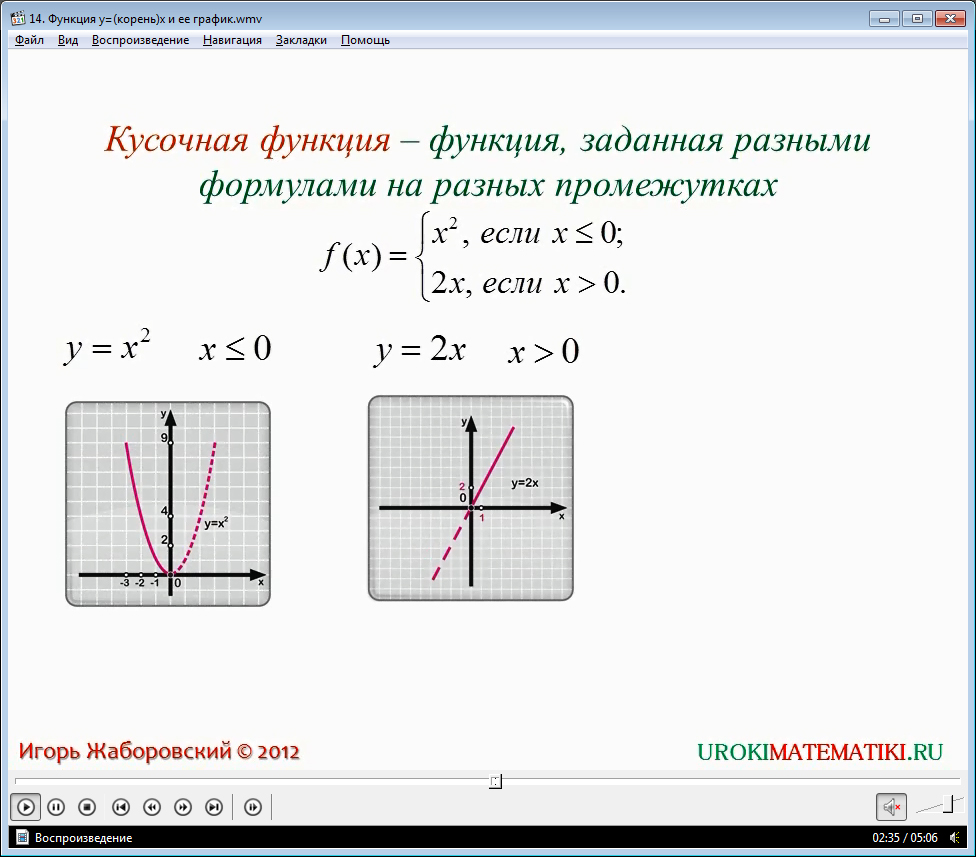
К примеру, ранее вам уже приходилось иметь дело с кусочными функциями.
Кусочная функция – это такая функция, которая на разных её промежутках описывается разными формулами.
{ y = 3x, при х ≤ 1
{ y = x3, при х > 1
Для того чтобы построить кусочную функцию, нам для начала нужно построить еще две обычных: y = 3x и y = x3. Сначала построим первую, и условно проведем вертикальную черту в точке x = 1, а всё, что находится правее неё, сотрем. На другом рисунке построим вторую функцию и, аналогично с первой мысленно проведем такую же вертикальную черту в той же точке, и сотрём всё, что находится слева от нее (включая значение и в самой точке, строго следуя условиям уравнений). И последним шагом будет нанесение на одну координатную плоскость нарисованных нами двух функций.
С примером построения подобной функции можно познакомиться в видеоуроке.
Как бы странно это не звучало, но в нашем мире очень часто встречаются функции, просто мы их не замечаем. Мало того, абсолютно всё, что нас окружает, можно описать с помощью формул. Потому важным шагом в изучении математики и геометрии является знание как можно большего количества функций.
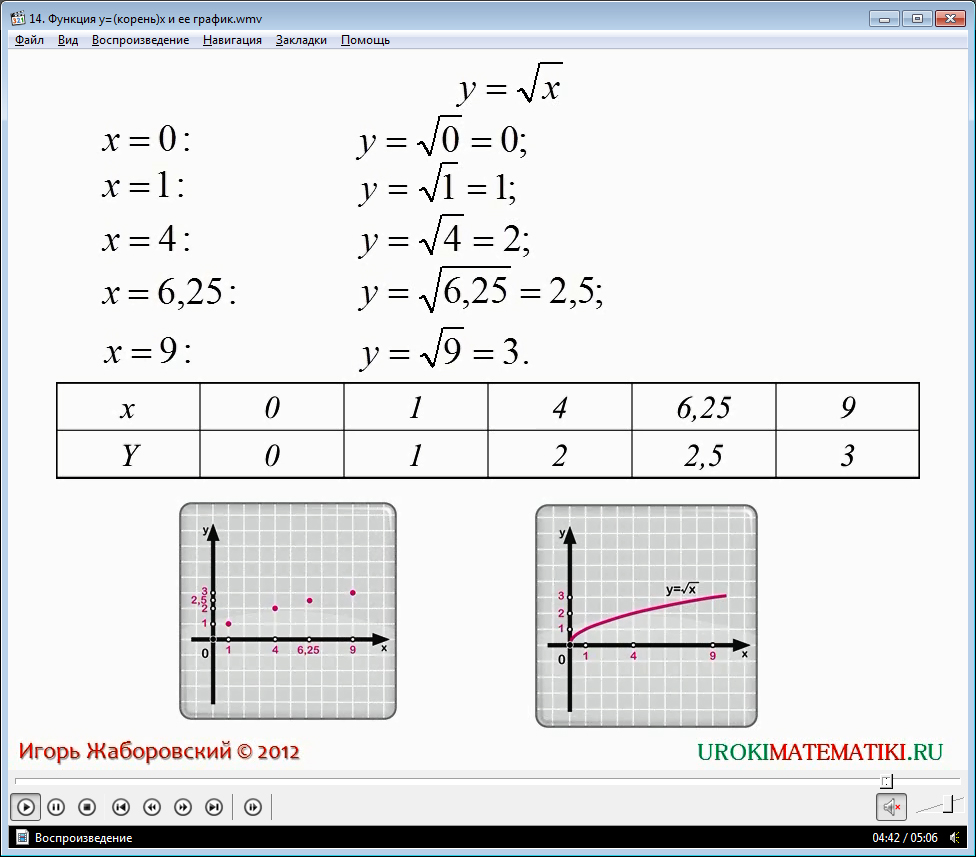
В данном видеоуроке мы познакомимся с функцией y = √x.
Для того чтобы это сделать, нам необходимо её для начала хотя бы увидеть. Для этого нам нужно её построить, потому проведем уже знакомые нам действия:
1) Найдем несколько значений функции (зависимой переменной) при разных значениях её аргумента (проще говоря, икса). Для простоты и удобства значения икса будем выбирать такими, чтобы от них легко брался корень, то есть 0 ,1 ,4, 9, 16.
Если x = 0, то y = √0 = 1, или же f(0) = √0 = 0,
если x = 1, то y = √1 = 1, или же f(1) = √1 =1,
если x = 4, то y = √4 = 2, или же f(2) = √4 = 2,
если x = 9, то y = √9 = 3, или же f(3) = √9 = 3,
если x = 16, то y = √16 = 4, или же f(4) = √16 = 4.
2) Теперь нанесем эти точки на координатную плоскость и соединим их в линию.
Как вы могли заметить, полученная фигура уже встречалась ранее, но она слегка повёрнута – её «рога» смотрят вправо, а не вверх. Действительно, функции y = √x и y = x в квадрате, очень похожи.
Замечание: при выборе значений аргумента очень важно выбирать положительные числа, поскольку корень от отрицательного числа не имеет смысла, по крайней мере, пока что. На дальнейших этапах изучения математики вы познакомитесь с понятием «мнимая единица» и смело сможете брать корень от любого числа.
Пример и детальное построение функции y = √x вы сможете увидеть в видеоуроке.
Для закрепления материала и лучшего его освоения рекомендуется сделать несколько упражнений:
1) Нарисовать графики функций: y = C, y = kx, y = km + m, y = x2, y = -x2
2) Нарисовать и вырезать график функции y = x2, нарисовать график функции y = √x и убедиться в том, что они идентичны, за исключением поворота на 45 градусов.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10336 |
| Номер материала | 538 |