
Урок "Свойства квадратных корней"

Краткое описание документа:
В этой главе мы познакомимся с еще одним математическим действием – извлечением корня из положительных чисел. Оно, как и все остальные, имеет ряд свойств, которые мы сейчас разберем.
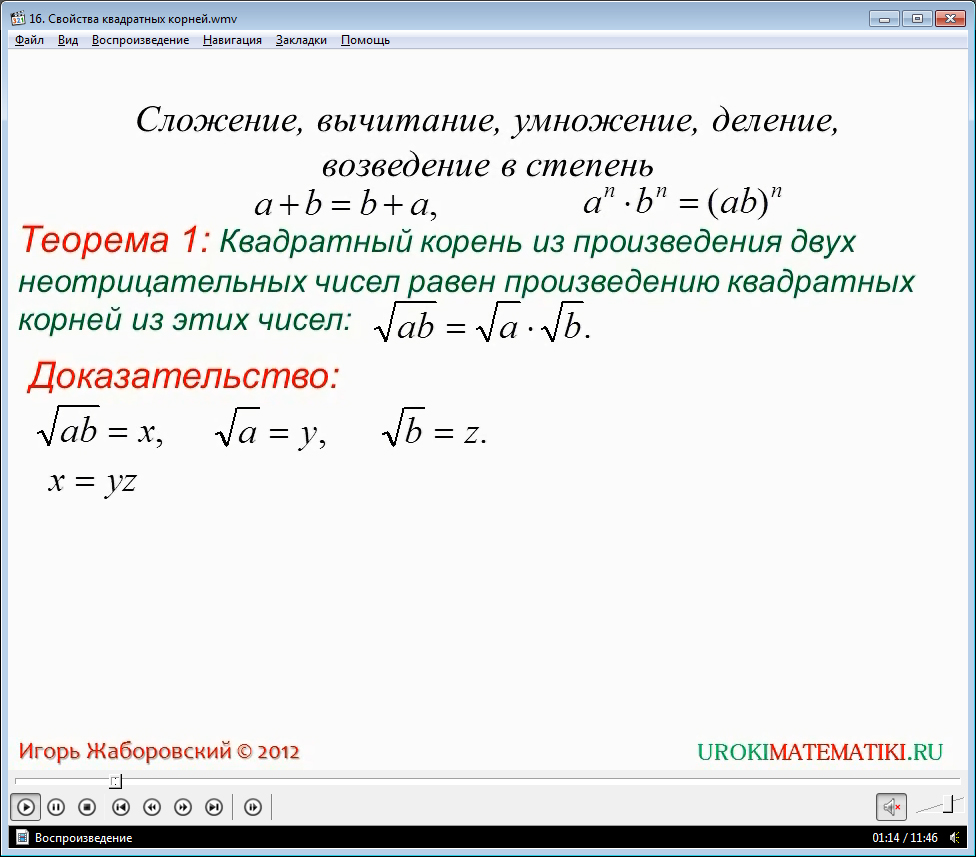
1) Квадратный корень произведения чисел равен произведению квадратных корней этих чисел. В математическом виде это свойство выглядит как:
√(a * b) = √a * √b
Доказательство:
Пускай √(a*b) = x, √a = y, √b = z, где все числа – положительные.
Нужно доказать, что выполнятся равенство x = y * z
Для этого выразим x2, y2 и z2:
x2 = a * b, y2 = a, z2 = b
Тогда x2 = y2 * z2 или x2 = (y * z)2
Исходя из того, что квадраты чисел равны, и сами числа равны (x = y * z)
Практическое применение этого свойства можно представить в виде:
√3 * √4 = √(3 * 4) = √12
2) Второе свойство гласит, что справедливо равенство √(a/b) = √a/√b, если a ≥ 0 и b > 0. То есть корень дроби равен дроби от корней.
Доказательство:
Как и при доказательстве прошлого свойства, воспользуемся заменами:
√(a/b) = x, √a = y, √b = z
Нам необходимо, чтобы выполнялось равенство x = y/z
Выразим x2, y2 и z2:
x2 = a/b, y = a, z2 = b
Тогда x2 = y2/z2 или же x2 = (y/z)2
И в итоге получаем то, что и требовалось доказать – x = y/z
Разберем несколько примеров, которые наглядно покажут, как можно использовать данные свойства для облегчения решения примеров.

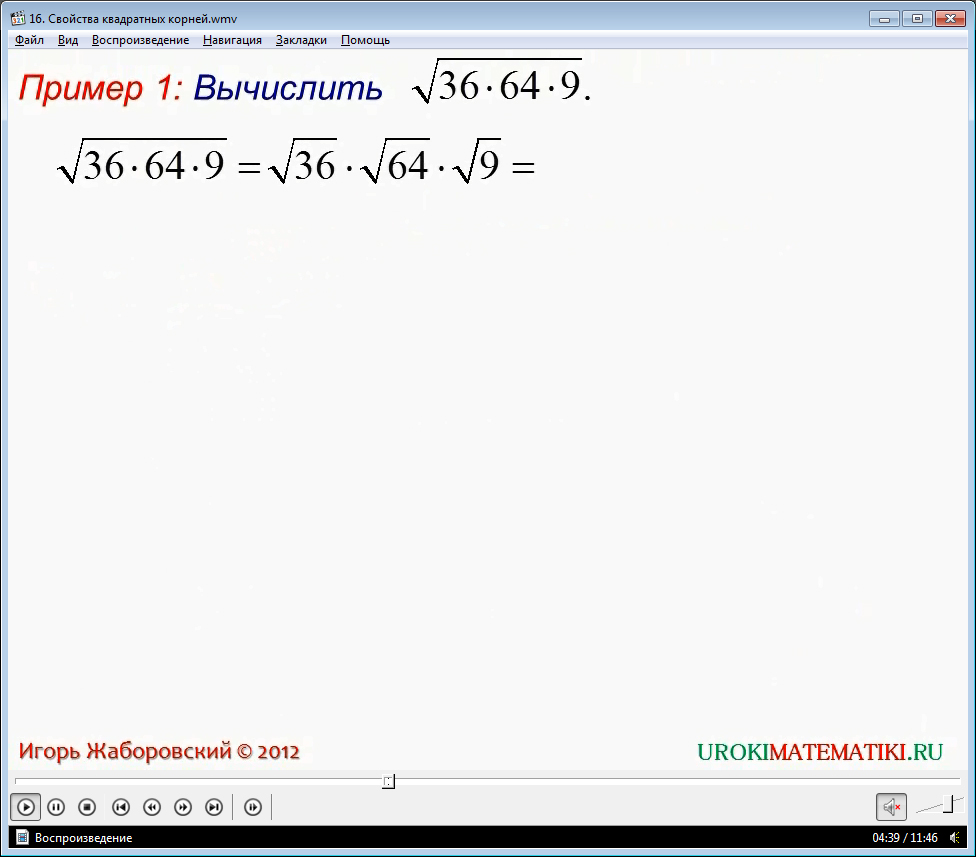
Пример 1
Вычислить √(36 * 121 * 9)
√(36 * 121 * 9) = √36 * √121 * √9 = 6 * 11 * 3 = 198
Здесь мы воспользовались первым свойством. Конечно, можно было бы сначала перемножить числа 36, 121 и 9, а потом из получившегося вычесть корень, но не всегда под рукой есть калькулятор, да и воспользоваться им можно не везде.
Пример 2
Вычислить значение под корнем десяти целых девяти шестнадцатых
Приведем к общему знаменателю:
10(9/16) = 10 + 9/16 = 160/16 + 9/16 = 169/16
Далее воспользуемся вторым свойством и элегантно решим пример:
√(169/16) = √169/√16 = 13/4 = 1(1/4)
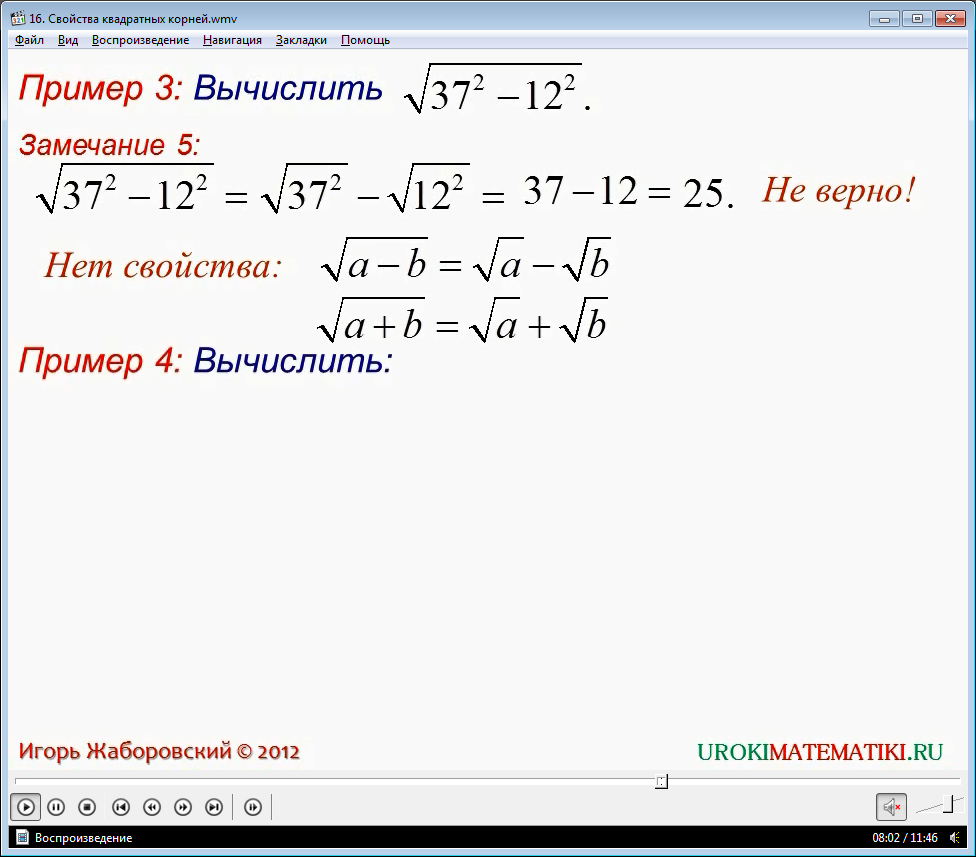
Пример 3
Вычислить √(372 - 122)
Для наглядности того, что всегда по возможности намного выгоднее и быстрее пользоваться свойствами корней, чем решать «в лоб», «победим» этот пример двумя способами.
Первый способ
Посчитаем квадраты чисел 37 и 12
372 = 1369, 122 = 144,
372 – 122 = 1369 – 144 = 1225
И с помощью калькулятора или таблицы квадратов запишем
√1225 = 35
Второй способ
Воспользуемся формулой упрощенного умножения для разности квадратов
a2 – b2 = (a – b) * (a + b)
372 – 122 = (37 – 12) * (37 + 12) = 25 * 49
Теперь воспользуемся первым свойством и перепишем
√(25 * 49) =√25 * √49 = 5 * 7 = 49
Таким образом, во втором способе нам не понадобились ни калькулятор, ни таблица квадратов, достаточно было лишь знание свойств квадратных корней и таблицы умножения.
Чтобы предотвратить одну из самых частых ошибок, следует заметить, что свойств квадратных корней всего два, и в них присутствует только умножение и деление. Многие пытаются использовать в корне неверные формулы:
√(a2 + b2) = √a2 + √b2
√(a2 – b2) = √a2 - √b2
Пример 4
Следует отметить, что рассмотренные нами равенства в свойствах могут использоваться как слева направо, так и справа налево. Это означает, что можно из произведения под корнем делать произведение корней, и наоборот. То есть, справедливы и идентичны по равноправию формулы:
√(a * b) = √a * √b и √a * √b = √(a * b)
√(a/b) = √a/√b и √a/√b = √(a/b),
a) Вычислить√24 * √6
√24 * √6 = √(24 * 6) = √144 = 12
b) Вычислить√24 / √6
√24\√6 = √(24/6) = √4 = 2
Также есть еще одно небольшое, но иногда очень полезное свойство. Если a≥0 и n – натуральное число, то
√a2n = an
Это равенство доказывается очень просто. Квадратный корень – это тоже в какой-то мере обычная степень. Если квадрат и куб числа мы записываем как a2 и a3, то квадратный и кубичный корень записываем как 2√a(принято писать просто √a ) и 3√a.
Квадратный, кубичный, да и корень любой степени можно не рисовать, а записывать просто в степень числа.
√a = a1\2
3√a = a1\3
и так далее.
Если же у нас число под корнем степени m стоит в какой-то степени n, то записать это можно как:
m√an = an/m
Потому, если у нас есть √a2n то мы просто запишем как a2n/2, сократим двойки и получим просто an.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6154 |
| Номер материала | 540 |