
Урок "Свойства функции y=√x"

Краткое описание документа:
В предыдущий раз мы познакомились с этой функцией и её видом. Сейчас же мы более детально поговорим о свойствах, которые вытекают из её геометрического вида – параболы.
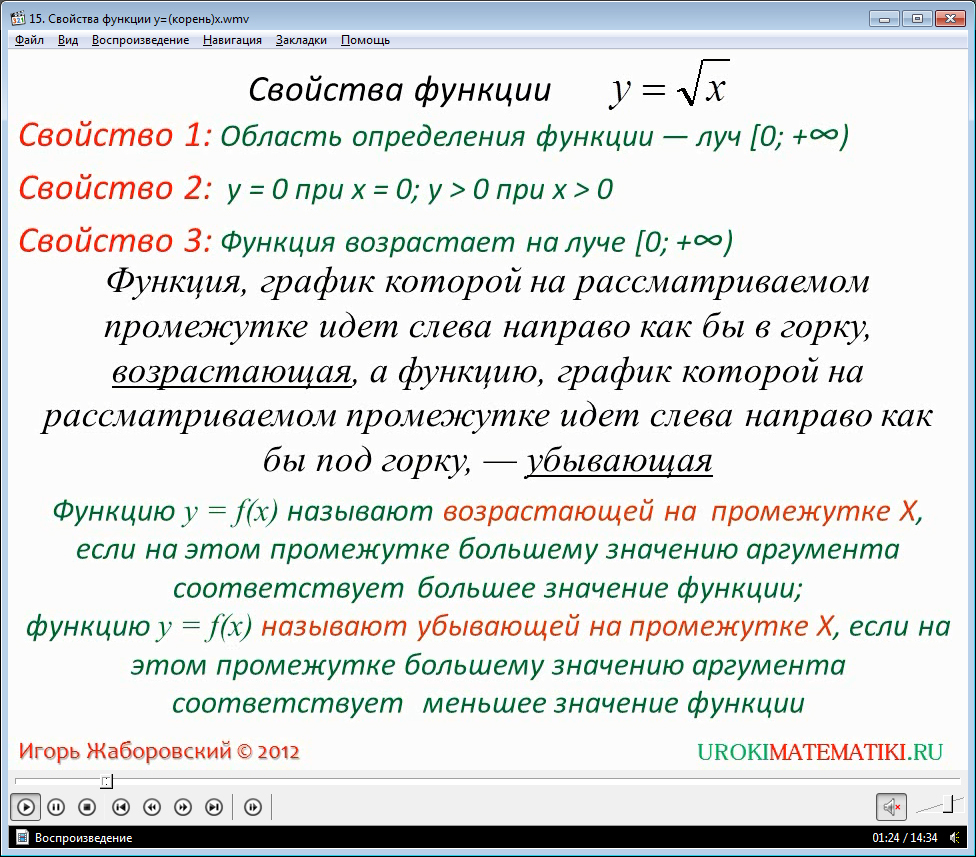
1) Функция определена в области [0;+∞);
Это свойство говорит нам о том, что икс принимает значения от нуля и до бесконечности. Самым главным здесь является то, что все значения строго положительные, и игрик просто не существует при значениях x<0.
2) x=0 при y=0; y>0 при x>0;
Это свойство следует понимать как то, что функция берет начало в координатах [0,0], а при увеличении значения аргумента (икса) увеличивается и значение самой функции.
3) На промежутке [0;+∞) функция возрастает;
Если представить себе график функции как настоящую горку и отправиться по ней в путешествие в сторону увеличения икса, то мы всегда будем подниматься всё выше и выше. Это и есть свойство возрастания функции.
К данному примеру это не относится, но если взять другую, убывающую функцию, то путешествие по ней (опять же, в сторону увеличения икса) будет легче, чем в первом случае, потому что нам придется все время спускаться, тратя меньше сил.
4) ymin= 0 при x = 0; ymax не существует
ymin– наименьшее значение функции
ymax – наибольшее значение функции
Как мы уже заметили выше, функция начинает своё существование в начале координат. Именно там и находится её наименьшее значение, которое она может принимать. А наибольшего значения не существует, потому что она всегда возрастает, сколь большим бы мы не брали значение аргумента. Но если же мы поставим какие-то рамки, например, x = [0,9], то ymax примет значение 3.
5) Функция y = √x – непрерывная.
Это свойство говорит о том, что у функции нет разрывов. Можно провести аналогию с электрическим проводом. Если представить, что график функции – это провод, то он сплошной и проводит электричество только в том случае, если не имеет разрывов. Если его разорвать, он уже ни на что не сгодится. Так же и с функциями – они непрерывны только в том случае, если не имеют разрывов.
В предыдущем уроке говорилось о том, что две функции y = x2 и y = √x очень похожи (они совпадают, если повернуть любую из них). Это так, и на этом схожести не заканчиваются. Все свойства, описанные выше для функции y = √x абсолютно идентичны и для функции y = x2, что сильно смущало математиков, потому что они – люди очень придирчивые к мелочам. По их мнению, не может существовать двух разных функций с одинаковыми свойствами.
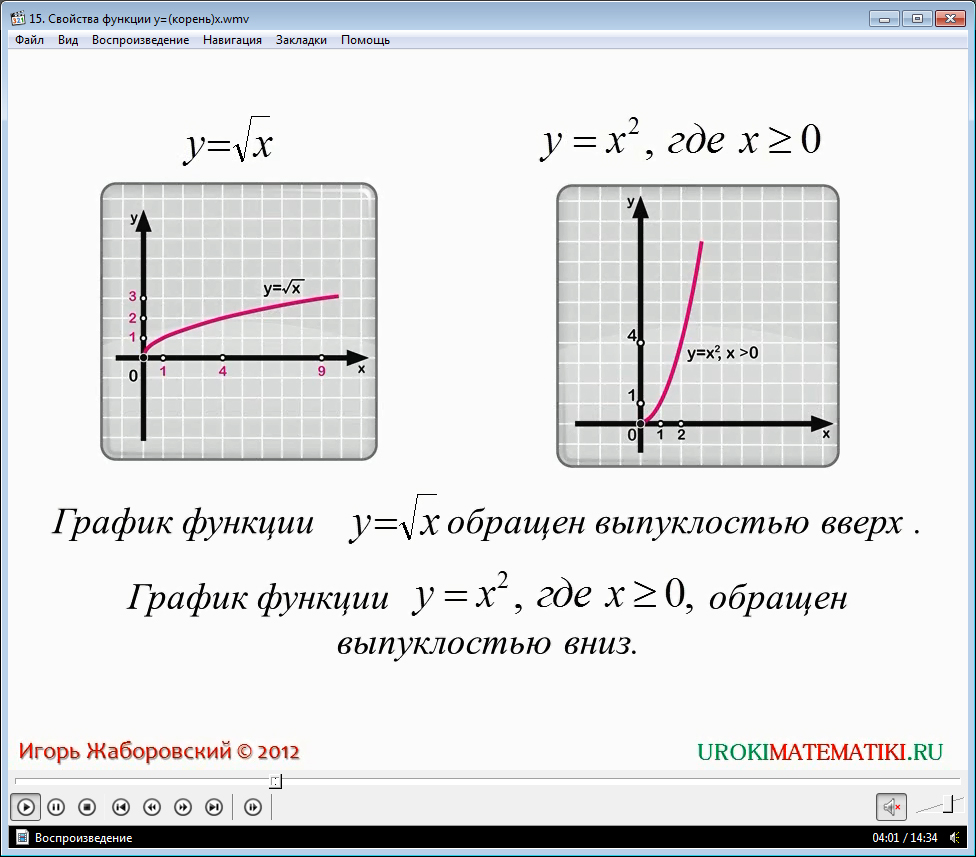
Они обнаружили принципиальные различия между этими двумя функциями. Если говорить определением, то разница заключалась в том, куда направлена выпуклость функции – вниз или вверх. Выпуклость можно себе представить как тарелку. Если тарелка стоит донышком вниз – то выпуклость направлена вниз. Если тарелка стоит донышком вверх – то и выпуклость направлена вверх.
На функциях это выглядит таким образом: мы берем две любые точки на графике (лучше всего первую взять в начале координат, а другую как можно дальше) и соединяем их прямой линией. Получившуюся фигуру закрашиваем и получаем выпуклость. На графике функции y = x2 выпуклость будет направлена вниз, а у функции y = √x – вверх.
В видеоуроке выпуклости детально проиллюстрированы.
Разберем несколько примеров типичных задач.
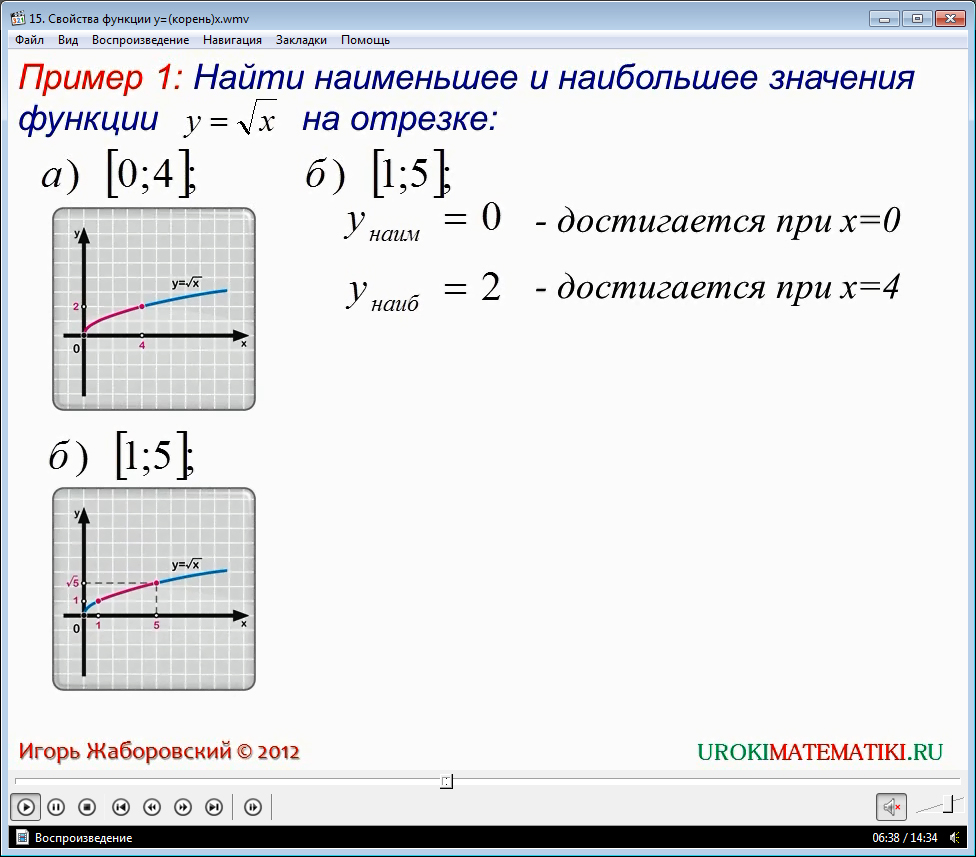
Найти максимальное и минимальное значение функции y = √x на отрезке
- x = [0,9]
- x = [2,4]
Решается эти задачи очень просто, если помнить о том, что наша функция непрерывно растет вверх вместе с увеличением её аргумента (икса). Потому, если у нас дан любой отрезок, имеющий начало и конец, то минимальное значение функции всегда будет в начале этого отрезка, а максимальное - в конце.
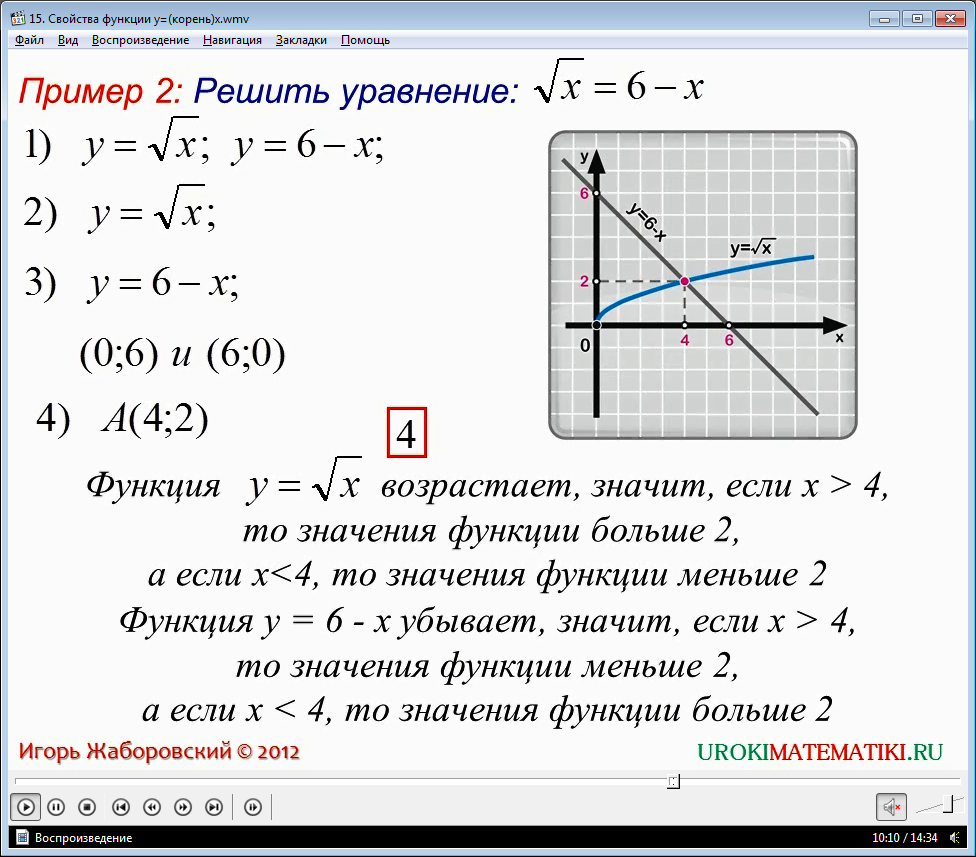
Так, для примера, а ymin= 0, а ymax= √9 = 3,
А в примере bymin= √2, aymax= √4 = 2
Множество других решений задач вы можете увидеть в видеоуроке.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 3379 |
| Номер материала | 539 |