
Урок "Множество действительных чисел"

Краткое описание документа:
Множество действительных чисел - это совокупность дополнения рациональных чисел иррациональными. Обозначается это множество буквой R, а в качестве символа принято использовать запись (-∞, +∞) либо (-∞,∞).
Описать множество действительных чисел можно следующим образом: это множество конечных и бесконечных десятичных дробей, конечные десятичные дроби и бесконечные десятичные периодические дроби – рациональные числа, а бесконечные десятичные и непериодические дроби – иррациональные числа.
Любое действительное число можно указать на координатной прямой. Также уместно и обратное утверждение: любая точка на координатной прямой имеет действительную координату. На математическом языке это звучит так: между множеством точек координатной прямой и множеством R действительных чисел можно установить взаимно однозначное соотношение. Для самой координатной прямой зачастую используют термин «числовая прямая», так как координатная прямая является геометрической моделью множества действительных чисел.
Оказываться, что ваше знакомство с координатной прямой было давно, но пользовать ею вы начнете только сейчас. Почему? Ответ вы сможете найти в примере из видеоурока.
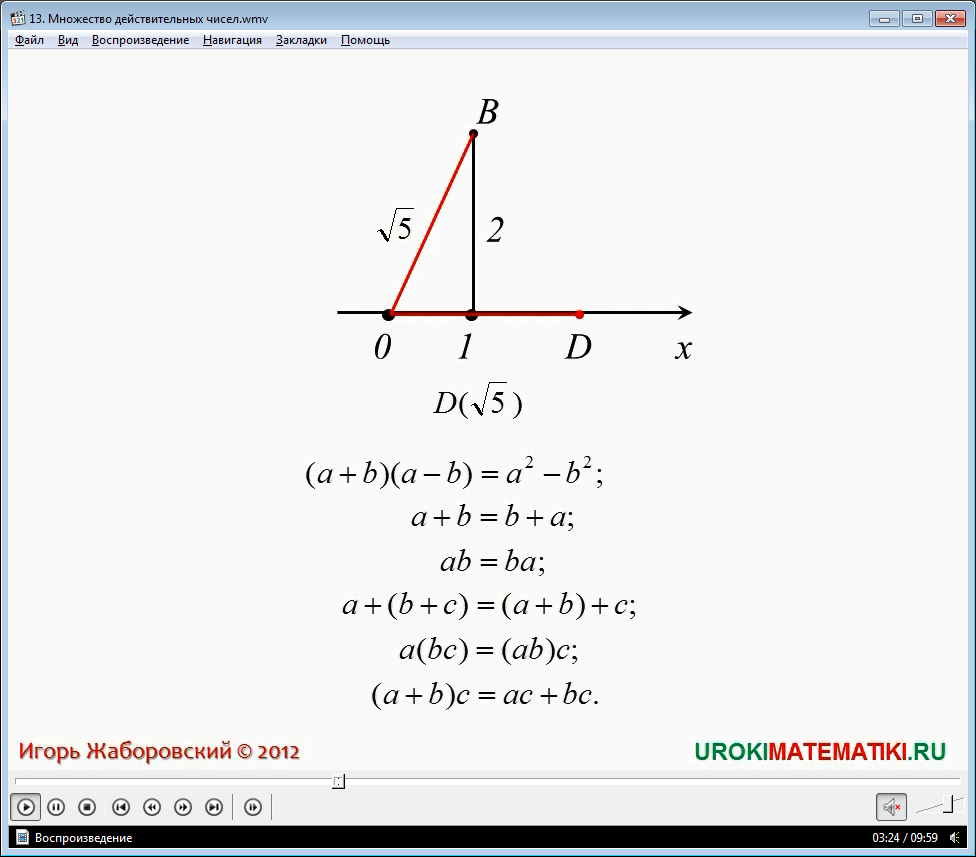
Известно, что для действительных чисел a и b выполняются уже хорошо известные вам законы сложения и умножения: коммуникативный закон сложения, коммутативный закон умножения, ассоциативный закон сложения, дистрибутивный закон умножения относительно сложения и другие. Проиллюстрируем некоторые из них:
a + b = b + a;
ab = ba;
a + (b + c) = (a + b) + c;
a(bc) = (ab)c;
(a + b)c = ac + bc
Также выполняются следующие правила:
1. В результате произведения (частного) двух отрицательных чисел получается число положительное.
2. В результате произведения (частного) отрицательного и положительного числа получается число отрицательное.
Сравнить действительные числа друг с другом можно, опираясь на определение:
Действительное число a больше или меньше действительного числа b, в том случае, когда разность a – b является положительным или отрицательным числом.
Записывается это так: a > b, a < b.
Это значит, что а является положительным числом, а b – отрицательное.
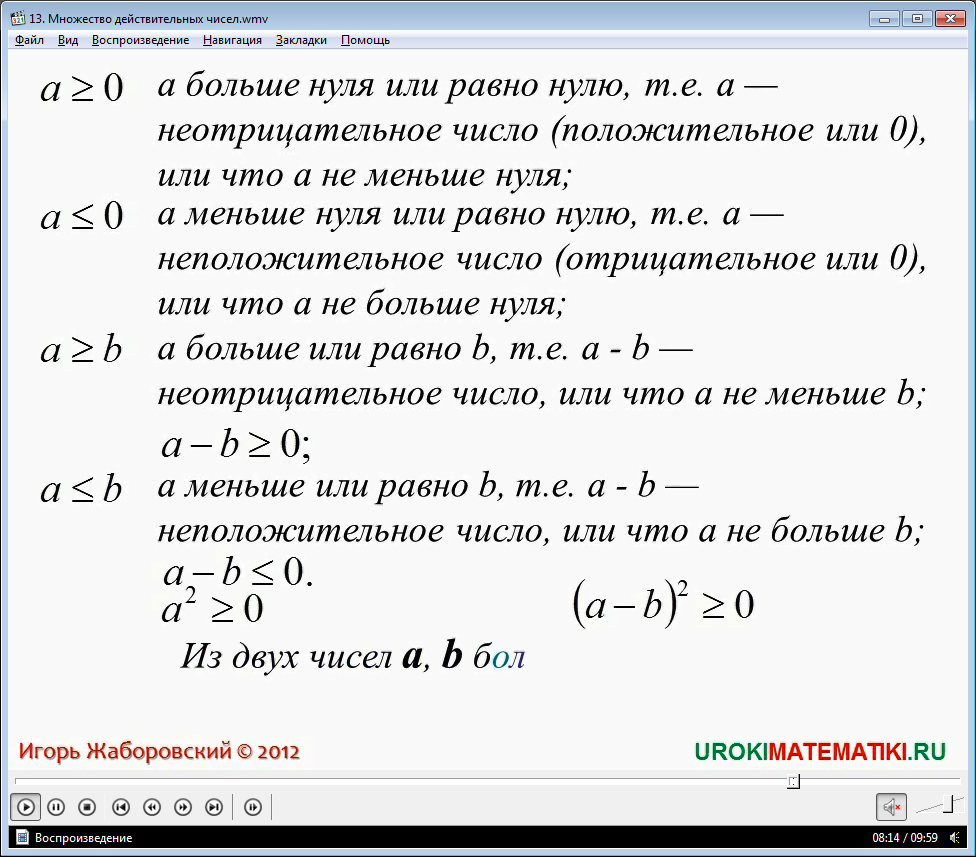
То есть, в случае, когда a > 0 => a положительно;
a < 0 => a отрицательное;
a > b, то a – b положительно => a – b > 0;
a < b, то a - b отрицательное => a – b < 0.
Помимо знаков (<; >) строгих неравенств, используются и знаки нестрогих неравенств – (≤;≥).
Например, для любого числа b, выполняется неравенство b2 ≥ 0.
Примеры сравнения чисел и расположения их в порядке возрастания Вы можете в видеоуроке.
Благодаря геометрической модели множества действительных чисел – числовой прямой, операция сравнения выглядит особо наглядно.
Основное свойство алгебраической дроби
Мы продолжаем знакомство с алгебраическими дробями. Если на предыдущем уроке речь шла об основных понятиях, то на этом уроке вы узнаете об основном свойстве алгебраической дроби. Определение основного свойства дроби известно из курса математики 6 класса (сокращение дробей). В чем же оно состоит? Часто при решении задач, уравнений возникает необходимость преобразовать одну «неудобную» для вычислений дробь в другую, «удобную». Именно для выполнения таких преобразований и необходимо знать её основное свойство и правила изменения знаков, с которыми вы познакомитесь, просмотрев видеоурок.

Значение обыкновенной дроби останется неизменным при умножении или делении числителя и знаменателя на одно и то же число (кроме нуля). В этом и состоит основное свойство дроби.
Рассмотрим пример:
7/9 = 14/18
Имеем две дроби, тождественно равные друг другу. Числитель и знаменатель в данном случае умножили на 2, при этом значение дроби не изменилось.
Что происходит с дробью при делении числителя и знаменателя на одно и то же число, вы узнаете из видеоурока.
Алгебраическая дробь – это, в принципе, та же самая обыкновенная дробь, над ней можно выполнять те же действия, что и над обыкновенной.
Выражение, стоящее в числителе, и выражение, стоящее в знаменателе дроби, можно домножить или разделить на одно и то же буквенно-цифровое выражение (многочлен или одночлен), одно и то же число (кроме нуля: если выражение или число, стоящее в знаменателе дроби, умножить на ноль, он примет нулевое значение; а, как известно, на ноль делить нельзя). Такое преобразование алгебраической дроби называют её сокращением. В этом и состоит основное свойство алгебраической дроби. Как оно реализуется на практике – вы можете узнать из видеоурока.
Преобразование дробей в дроби с одинаковыми знаменателями называют приведением дробей к общему знаменателю. Для выполнения данного действия необходимо выполнить определенную последовательность действий, состоящую в следующем:
• Разложив все знаменатели на множители , определяем НОК для числовых коэффициентов.
• Записываем произведение, с учетом НОК коэффициентов и всех буквенных множителей. Если множители одинаковые, берём множитель один раз. Из всех степеней, у которых одинаковые основания, берем множитель с максимальным показателем степени.
• Находим значения, являющиеся дополнительными множителями для числителя каждой из дробей.
• Для каждой дроби определяем новый числитель - как произведение старого числителя на дополнительный множитель.
• Записываем дроби с новым числителем, который определили, и общим знаменателем.
Пример 1: Привести следующие дроби a/4b2 b a2/6b3 к общему знаменателю.
Решение:
Для начала определим общий знаменатель. (Он равен 12b2).
Затем, следуя алгоритму, определим дополнительный множитель для каждой из дробей. (Для первой – 3b, для второй – 2).
Выполнив умножение, получим результат.
(a*3b)/(4b2*3b) = 3ab/12b3 и (a2*2)/(6b2*2) = 2a2/12b2 .
Пример 2: Привести дроби c/(c – d) и c/(c + d) к общему знаменателю.
Решение:
(c+d)(c-d)=c2-d2
c*(c + d)/(c – d)(c + d) = (c2 + cd)/(c2 – d2)
c*(c – d)/(c + d)(c - d) = (c2 – cd)/(c2 – d2)
Более подробное решение аналогичных примеров вы найдете в видеоуроке.
Основное свойство алгебраической дроби имеет следствие в виде правила изменения знаков:
a – b/c – d = b – a/d - c
В этом случае числитель и знаменатель дроби умножили на -1. Аналогичные действия можно производить не со всей дробью, а только с числителем или только со знаменателем. Как изменится результат, если, например, только числитель или только знаменатель умножить на -1, вы узнаете, просмотрев видеоурок.
Теперь, изучив основное свойство алгебраической дроби и вытекающее из него правило, нам по силам решать более сложные задачи, а именно: вычитание и сложение дробей. Но это уже тема следующего урока.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 7484 |
| Номер материала | 537 |