
Презентация "Равенство векторов"

Краткое описание документа:
Презентация на тему «Равенство векторов» является прекрасным интерактивным учебным материалом, использование которого на уроках в средней школе приведет к значительной оптимизации учебного процесса и сделает его более интересным и продуктивным. Информация, представленная в данной презентации, представляет собой материал, являющийся продолжением темы «Вектор». Вся информация имеет четкую и логичную структуру, а слайды представлены по мере усложнения учебного материала.
Для более полного усвоения материала, каждое утверждение подтверждено буквенными выражениями и графическими изображениями. Возможность использования интерактивный материал имеет огромное количество плюсов, так как значительно экономится время, которое учитель обычно тратит на рисование и писание на доске. Все основные определения представлены взору учащихся и могут быть переписаны с доски, а не под диктовку учителя. Также при необходимости существует возможность вернуться к тому или иному уже рассмотренному слайду и еще раз обратить внимание на материал, представленный на нем, что исключает необходимость воспроизводить стертый с доски материал еще раз.

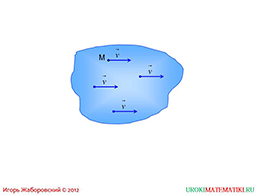
слайды 1-2 (Тема презентации "Равенство векторов", пример)
На втором слайде презентации представлены графические изображения четырех векторов, лежащих в одной плоскости, направленных в одном направлении, и имеющих одинаковые названия. При более внимательном рассмотрении становится ясно, что каждый из векторов имеет одинаковую длину.


слайды 3-4 (определение коллиниарных векторов, пример)
Следом идет слайд, на котором находится несколько определений, для более полного усвоения которых, представлены как графические изображения, так и буквенные выражения. Первое определение, представленное на третьем слайде, раскрывает понятие коллинеарного вектора. Согласно определению, коллинеарными называются вектора, которые лежат либо на одной прямой, либо на прямых, которые являются параллельными друг другу.
В связи с тем, что нулевой вектор представляет собой точку, через которую можно провести бесконечное множество прямых, в том числе и прямую, которая будет параллельна другой прямой, на которой лежит тот или иной вектор, то нулевой вектор можно считать коллинеарным абсолютно любому вектору. Далее следует информация, смысл которой заключается в том, что два коллинеарных вектора могут быть направлены как в одном направлении, так и в противоположных направлениях. В этом случае их называют сонаправленными или противоположно направленными. Примерами служат изображения нескольких векторов, имеющих различное направление, а также на слайде презентации показано, как правильно обозначать сонаправленные и противоположно направленные вектора.
На четвертом слайде презентации даны различные вариации того, как три коллинеарных вектора могут быть направлены по отношению друг к другу. На первом примере представлены три вектора, которые являются соноправленными, на втором и третьем примере показаны три вектора два из которых являются сонаправленными, а третий противоположно направленным. Примеры предназначены для того, что бы учащиеся научились определять взаимное направление двух векторов, зная их направление по отношению к третьему общему вектору, который не является нулевым.

слайд 5 (определение равных векторов)
На заключающем слайде презентации вниманию учащихся представлено условие, при котором два вектора можно назвать равными. Для того, что бы данное определение было хорошо понято и не вызвало никаких проблем при его усвоении и была подробно рассмотрена информация, представленная на предыдущих слайдах, без знания которой, понять условия равенства векторов будет очень сложно.
Основываясь на уже полученных знаниях, учащиеся должны понять, что равными можно считать два вектора только в том случае, если они являются сонаправленными и их длины равны. Знание условия равенства двух векторов является очень важным, так как оно будет очень часто применяться при решении различных задач на протяжении всего курса изучения предмета.
Применение новых нестандартных методов преподнесения материала играет чрезвычайно важную роль в оптимизации учебного процесса. Учащихся данной возрастной категории интересует все новое и интересное, а использование доски и мела никак нельзя назвать чем-то необычным.
Воспроизводиться данная презентация может не только с помощью компьютера, но также и с помощью специального оборудования, например, интерактивных досок, что значительно улучшит учебный процесс и сделает информацию, представленную на слайдах презентации доступной для аудитории, в которой находится большое количество учащихся.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 3782 |
| Номер материала | 357 |