
Презентация "Решение линейных уравнений с двумя переменными в целых числах"

Краткое описание документа:
Тема этого урока важна особенно, потому что является прикладной. Школьная математика подробно останавливается на уравнениях с одной переменной (их формат, решение). Однако ученикам не должно составлять сложности решать и элементарные уравнения с двумя переменными. Именно поэтому есть огромная необходимость остановиться на этой актуальной теме подробнее.


слайды 1-2 (Тема презентации "Решение линейных уравнений с двумя переменными в целых числах", пример)
Напомните, что координаты точки пишут в круглых скобках, где на первом месте находится «х», а на втором – «у». Наиболее удобно отмечать точки, когда координаты являются целыми числами (например, минус пять и девять, один и один, четыре и шесть). Далее покажите учащимся уравнение, где разность пять «х» и трёх «у» равняется двум. Являются ли перечисленные пары значений верными для данного уравнения?
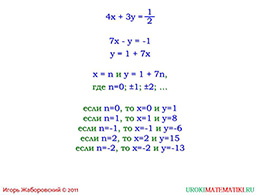

слайды 3-4 (примеры)
Далее дайте попробовать детям решить пример, когда свободный член является дробным числом. Вызовите одного ученика к доске, чтобы он наглядно показал решение, и подскажите, где необходимо исправить ошибки.
Далее стоит подробнее остановиться на уравнении, где разность семь «х» и «у» равняется минус одному. Решить данное уравнение будет удобнее всего, находя значение «у», потому что перед данной переменной нет коэффициента, а значит, не придётся делать деление.
Выражаем «у» через «х» и видим, что «х» может иметь бесконечное множество значений (переменная «n»). То есть, если «n» равняется нулю, то и «х» ему равняется, а функция будет равна единице. Спросите у учеников, как будет выглядеть график данной функции. Далее варьируйте значение «х» от минус двух до двух.
Оба использованные примеры сравните со стандартной записью линейного уравнения с двумя переменными, где сумма «ax» и «by» равняется «с». Уточните, где расположены независимые переменные, какие перед ними стоят коэффициенты, где расположен свободный член.


слайды 5-6 (примеры)
Рассмотрим более сложный пример, где необходимо вводить дополнительную переменную. Уравнение, где сумма двадцать «х» и три «у» равняется десяти. Пытаемся отождествить уравнение так, чтобы в скобках оказалось две переменные. Далее вводим переменную «k», которая равна сумме шести «х» и «у». Попробуем ввести ещё одну переменную «n», которая будет равна сумме «k» и «х». Тогда мы можем найти наиболее лёгкое значение «n», после чего находим «х» и, подставляя все значения, видим, чему равна переменная «у». В результате получаем, что «х» равно сумме минус десяти и трёх «n», а «у» равно разности семидесяти и двадцати «n». Переменная «n» может иметь бесчисленное множество значений (например, если «n» равно трём, то «х» равен минус одному, а «у» равен десяти). Чему будут равны переменные «х» и «у», если «n» является нулём?
Напоследок, рассмотрим задачу с книгами, где необходимо найти количество купленных книг, если известна общая сумма покупки, а также стоимость разных видов книг. В данном случае необходимо ввести две переменные. Попробуйте дать возможность ученикам самостоятельно решить данный пример. Если видите, что большинству это ещё составляет сложность, то вновь поэтапно анализируйте каждый шаг данной задачи, чтобы прийти к верному ответу. Для закрепления материала, задайте в конце учащимся вопросы по данной теме.
Обычно решение линейных уравнений с двумя переменными является сложной темой для большей части класса. Именно поэтому традиционная форма лекции не настолько эффективна, как метод проблемно-диалогического обучения. Таким способом вы вовлекаете учащихся в диалог, формирую тему и вопрос. Далее ученики накапливают знания в результате собственных открытий и так получают наиболее подлинный материал, который освоен ими максимально эффективно.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4463 |
| Номер материала | 217 |