
Презентация "Уравнения с двумя неизвестными"

Краткое описание документа:
Объявите учащимся тему урока, чтобы они понимали, что сегодня будут рассмотрены уравнения с двумя неизвестными. Уточните у школьников, какое различие между уравнением и неравенством, что такое переменные.


слайды 1-2 (Тема презентации "Уравнения с двумя неизвестными", пример)
Рассмотрим уравнение, где сумма «х» в квадрате и два «у» равняется шести. Мы видим, что оно содержит две переменные: «х» и «у». Именно такие примеры известны в математике как уравнения с двумя переменными. Попробуем подставить следующую пару чисел: например, два вместо «х» и один вместо «у». Решив уравнение, мы видим, что получили верное равенство. В данном случае подобранная пара чисел и является решением уравнения (их также называют «х» нулевое и «у» нулевое).

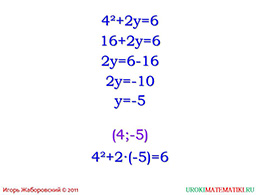
слайды 3-4 (решение уравнения, пример)
Далее необходимо дать чёткое определение того, что является решением уравнения. Расскажите о том, что «х» нулевое и «у» нулевое также называются частными выражениями уравнения, то есть при подстановке этой пары мы получаем верное уравнение (как в нашем примере).
Если даже значение «х» и «у» поменять местами (то есть пускай «х» равен единице, а «у» нулю), то мы не получим равное уравнение, поэтому данная пара чисел не подходит. Подходящая пара значений в итоге записывается в скобках, где первым значением является «х», а вторым – «у». Например, решение нашего уравнения мы запишем как (2; 1).
Если в наше уравнение вместо «х» подставить какое-то значение (например, четыре), то получаем уравнение с одной переменной, где мы можем найти «у». Таким образом, мы находим ещё одну пару чисел, которая является решением уравнения – (4; -5).
Получается, задача состоит в том, чтобы найти или изобразить на плоскости множество всех решений (ключевое слово – всех, пропусти нельзя ни одного, потому что их бывает бесчисленное множество).


слайды 5-6 (равносильные уравнения, свойства уравнений с двумя переменными)
Можно достаточно долго подбирать все возможные значения уравнения. Поэтому для начала стоит решить само уравнение в двумя переменными. Попробуем выразить переменную «у» с помощью переменной «х», перенося слагаемое «х» в квадрате в правую часть уравнения. Получили, то изначальное и полученное уравнения имеют одинаковое множество решений, поэтому они являются равносильными.
Далее стоит перечислить все свойства уравнения с двумя переменными, ссылаясь на наш пример. Первое свойство, которое говорит о равносильности данных при переносе переменных из одной части в другую со сменой знака. В нашем случае мы переносили «х» в квадрате из левой части в правую, меняя знак на минус.
Второе свойство позволяет обе части уравнения умножать и делить на число, отличное от нуля, оставляя уравнение равным. В нашем примере, мы делили обе части уравнения на число два, чтобы избавиться от коэффициента перед «у».
Последнее свойство позволяет нам делать тождественные преобразования в обеих или одной частях, что оставит уравнение равносильным. Какие тождественные преобразования известны? Это раскрытие скобок, приведение подобных и другие. Однако есть случаи, когда тождественные преобразования невозможны: как в указанном примере, где при наличии скобок мы видим, что областью определение не может быть ноль, а при раскрытии скобок область определения расширяется. Именно поэтому при решении уравнения важна проверка.
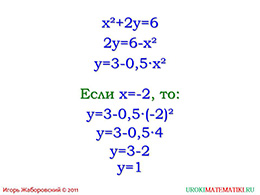

слайды 7-8 (примеры)
Вернёмся к нашему уравнению и вместо «у» подставим то значение, которое мы получили. Вместо значения «х» попробуем подставить значение минус два. Тогда областью значения будет один. Предложите учащимся решить данное уравнение, если «х» равен нулю или единице.
Уравнения с двумя переменными могут иметь множество значений или же иметь лишь одно решение, как выше упомянутый пример. Здесь мы видим, что правильной парой может быть только (0; 0).
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4049 |
| Номер материала | 215 |