
Урок "Функция y=x^3. Степенная функция с нечетным показателем"

Краткое описание документа:
Все алгебраические зависимости, имеющие вид у = (х)n именуются степенными функциями. Любая степенная функция представляет собой некоторую формулу взаимосвязи между двумя числовыми множествами, одно из которых представляет собой набор чисел другого множества, возведенные в определенную степень. В предыдущем видеоматериале мы ознакомились с общими принципами степенных зависимостей, а также изучили квадратичную функцию как представителя класса четных степенных функций.
Следует отметить, что из-за особых свойств степени любая степенная функция (как и многие другие математические конструкции) весьма зависит от четности самой степени. По этому признаку бесконечное множество степенных зависимостей можно поделить на две группы: четные и нечетные степенные функции. При этом разница между свойствами этих групп может быть довольно заметной.
Изучим функцию с нечетной степенью. Исключая вариант вырожденной степенной зависимости (с n = 1), простейшая функция с нечетной степенью имеет вид:
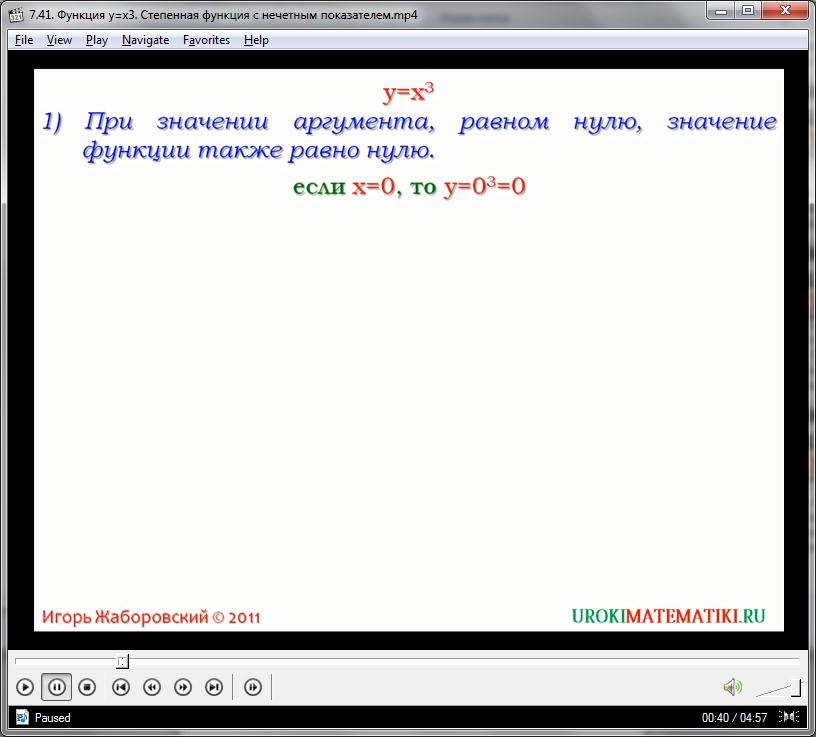
у = х3
Подобная зависимость именуется кубической функцией. На практике она часто представлена формулой нахождения объема куба:
V = а3
Первое свойство кубической зависимости вполне схоже с подобным свойством квадратичной функции – при нулевом значении аргумента значение самой функции так же будет равно нулю. На графике это обозначено принадлежностью центральной точки (0, 0) графику и кубической, и квадратной функций.
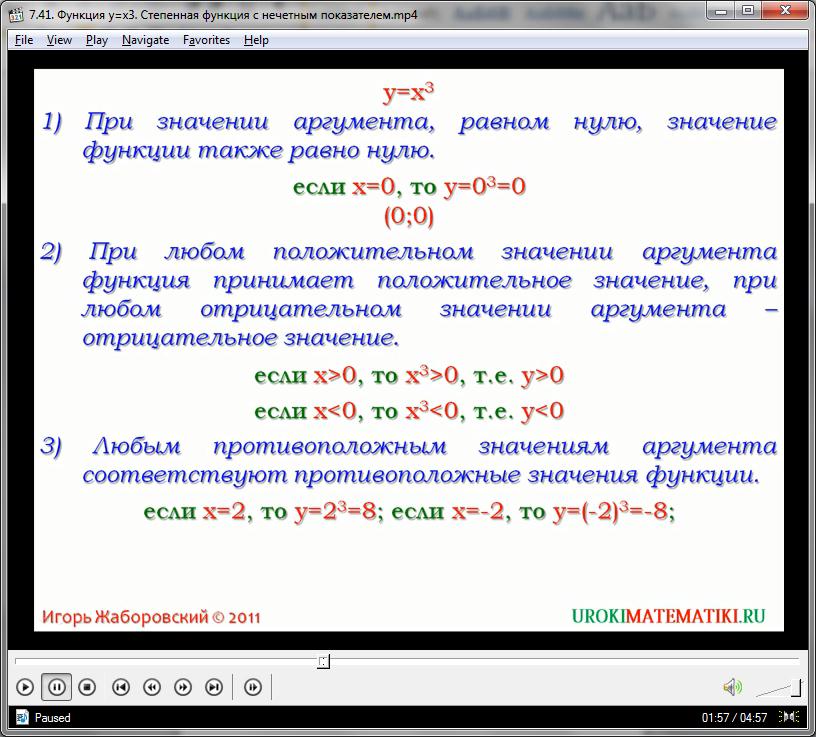
Дальше начинаются расхождения, вызванные нечетностью степени. Как известно, любая четная степень превращает выражение в строго положительное. А любая нечетная сохраняет исходный знак. Если аргумент кубической функции равен отрицательному числу, то и значение функции будет отрицательным. При положительных значениях аргумента, у также будет положительным. А это значит, что график кубической функции начинается в третьей четверти (-х, -у), и проходит через центр координат в первую четверть (х, у). Собственно говоря, начала и конца предполагаемая кривая иметь не будет – её концы уходят в бесконечность. Так как и область определения кубической функции, и область её значений лежат во всем множестве действительных чисел.
Третье свойство кубической зависимости гласит: любым противоположным аргументам х соответствуют противоположные значения у. Например, если а=2, с=-2, то:
у = х3 = а3
у = (2)3 = 8
у = (-2)3 = -8
Таким образом, график данной функции должен быть симметричным точке пересечения координатных осей, то есть – центру системы Декарта.
Для того, чтобы изучить график кубической зависимости, представленный на видео, построим его при помощи данной координационной сетки, воспользовавшись интервалом х (-2, у) (2, у):
у = х3
х = -2, у = (-2)3 = -8
х = -1, у = (-1)3 = -1
х = 0, у = (0)3 = 0
х = 1, у = (1)3 = 1
х = 2, у = (2)3 = 8
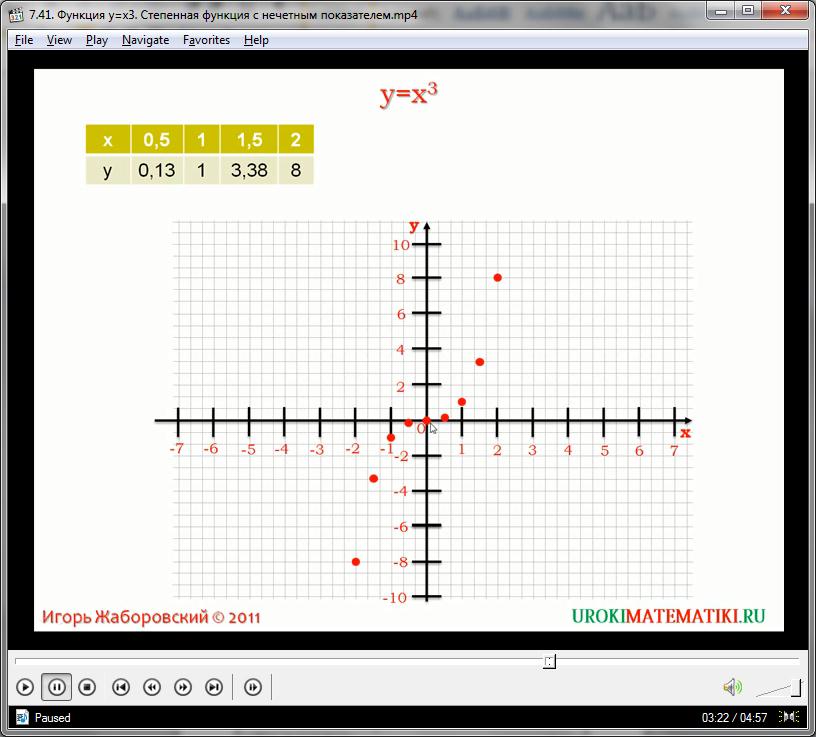
Отметив все точки и соединив их плавной кривой, мы получим искомый график кубической функции. Он представлен математической фигурой, именуемой кубической параболой. Она немного похожа на квадратичную: так же состоит из двух ветвей, тяготеющих к оси ординат, и общего центра, соединяющего ветви, и называемого вершиной параболы. В формулах без дополнительных коэффициентов (в чистых степенных функциях) вершина параболы всегда лежит в точке пересечения осей (0, 0).
Однако при этом правая ветвь кубической параболы идет от О по первой четверти вверх, а левая – симметрично, от точки О, в третью четверть, вниз. Обе устремляются во множество у.
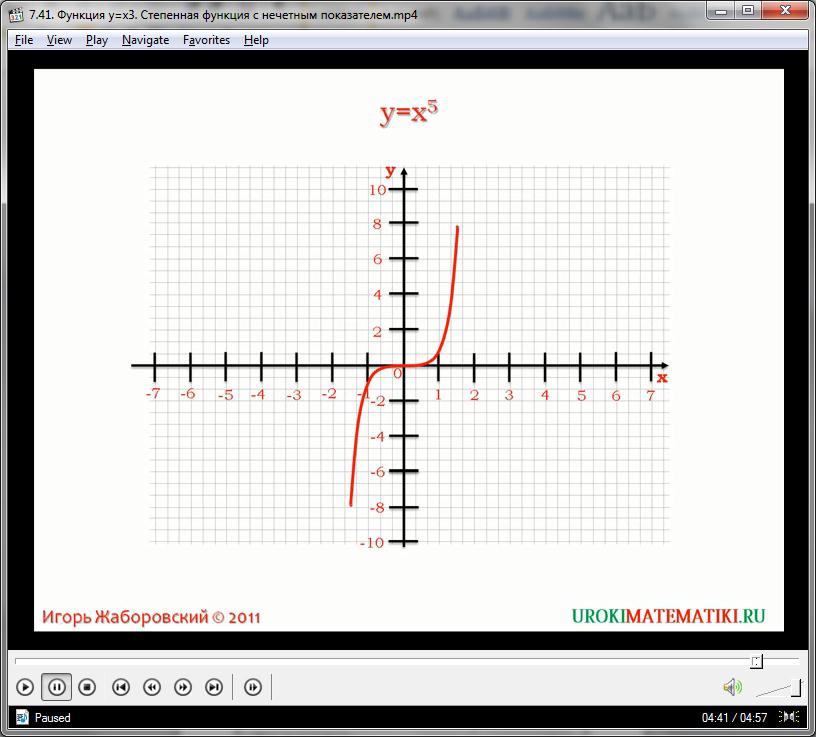
Любая степенная функция, имеющая нечетную степень аргумента, обладает такими же свойствами, как и кубическая. Графики степенных нечетных зависимостей схожи между собой – они представлены кубическими параболами. При повышении степени ветви графика меняются неравномерно: части параболы на интервалах от (-1, у) до (1, у) тяготеют к оси абсцисс, а остальные части (от единичного аргумента в бесконечность) – к оси ординат. Это поясняется тем, что аргументы, значение которых лежит между 0 и 1, сильно уменьшаются высокими степенями, и выходное значение у стремится к нулю. С другой стороны, все х, которые больше 1, дают очень быстрый прирост значениям функций при высокой степени.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 11205 |
| Номер материала | 473 |