
Урок "Уравнения с двумя неизвестными"

Краткое описание документа:
Большинство задач в математике ориентировано на решение стандартных уравнений, содержащих одну переменную. Иногда используется система двух и более уравнений, которые могут включать, соответственно, две и более переменные.
Однако изучим отдельное уравнение, содержащее в своем составе помимо числовых выражений два неизвестных абстрактных выражения. Например:
х2 + 2у = 6
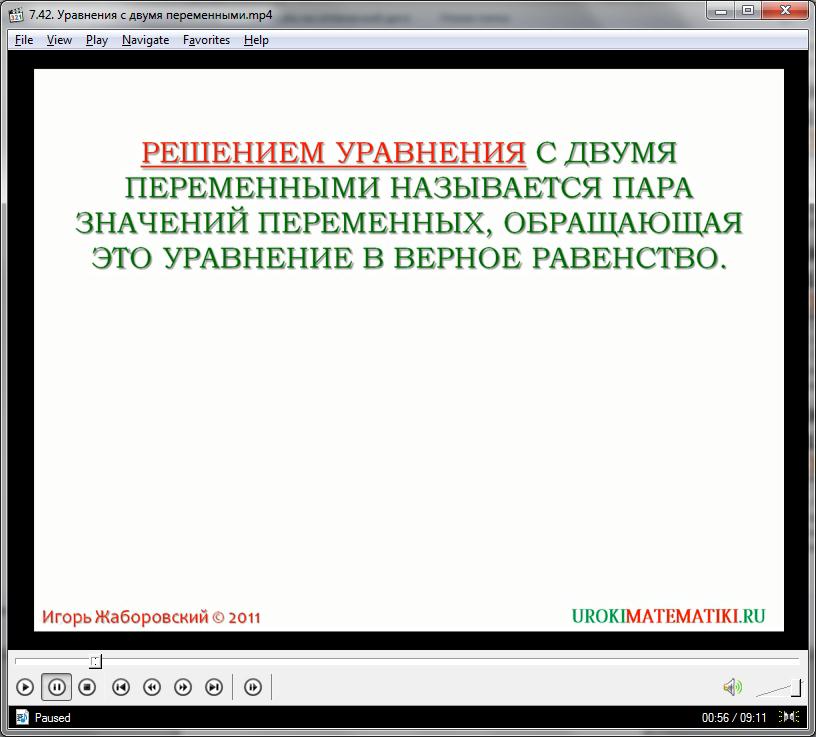
Любое подобное уравнение называется уравнением с двумя переменными. Решением подобного уравнения называется такая пара значений х и у, при которой все выражение преобразуется в равносильное правильное равенство. Используем такие значения для переменных:
х = 2
у = 1
Подставляя в наше уравнение, получим верное равенство:
х2 + 2у = 6
(2)2 + 2(1) = 6
4 + 2 = 6
Таким образом, пара чисел (2, 1) являются решением для уравнения.
х2 + 2у = 6. Отметим, что при записи решения необходимо указывать значения переменных в скобках через запятую, на первое место записывая значение х (это не строго, но утверждено).
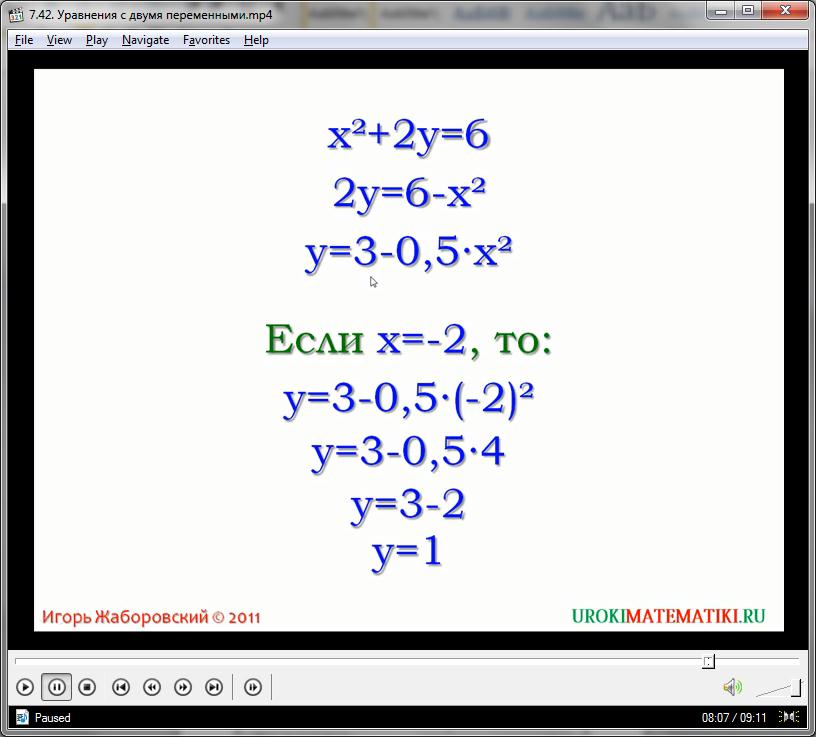
Решая первый пример методом подбора, легко найти ещё одну пару решений – например, воспользуемся значениями (4, -5):
х2 + 2у = 6
(4)2 + 2(-5) = 6
16 – 10 = 6
Пара чисел превратила уравнение в правильное равенство, значит, она так же соответствует решению данного уравнения.
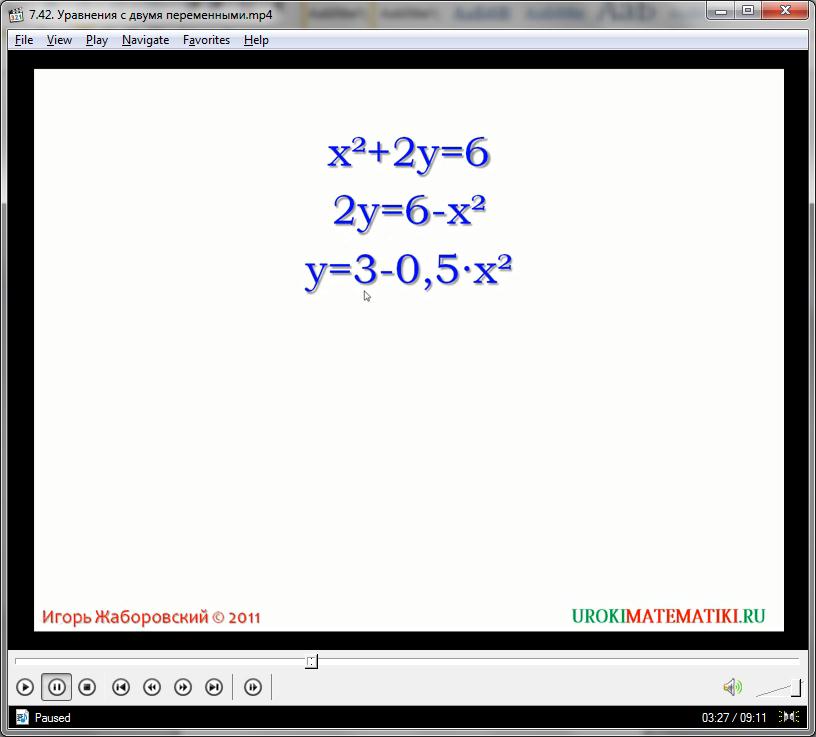
Как можно понять из видеоурока, уравнение с двумя переменными имеет множество решений, точнее, множество пар чисел, которые будут соответствовать критериям правильного ответа. Преобразуем первое уравнение следующим образом. Поделим все части равенства на 2:
х2 + 2у = 6
0,5х2 + у = 3
у = 3 – 0,5х2
Полученное выражение у = 3 – 0,5х2 является ничем иным, как функцией – зависимостью одной переменной от второй. Иначе говоря:
у = 3 – 0,5х2
у = f(х)
f(х) = 3 – 0,5х2
Как мы помним из видеоуроков, посвященных основам функций, любая зависимость характеризуется тремя элементами: множеством неких начальных аргументов, формулой преобразования, множеством полученных значений. В нашем уравнении множество всех реальных решений представлено парами значений х и у – то есть, парными элементами обеих множеств функции. При этом само уравнение представляет собой выражение зависимости между первой и второй переменной.
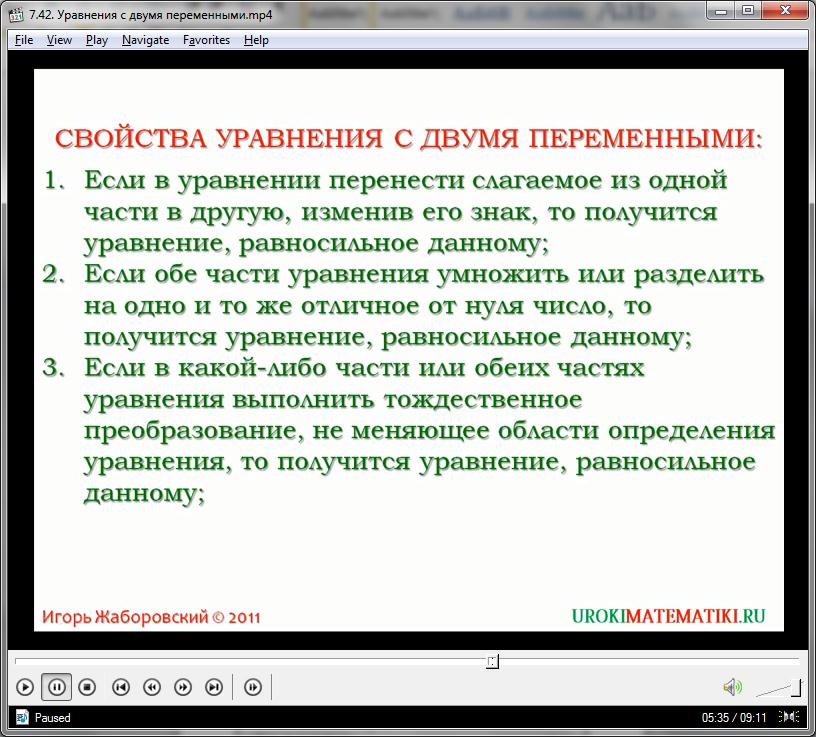
Помимо того, выражение у = 3 – 0,5х2 имеет точно такие же пары решений, как и х2 + 2у = 6 – поэтому, эти уравнения называются равносильными. Равносильные уравнения получаются в таких случаях:
- При осуществлении переноса слагаемых (с учетом инверсии знака) с одной части равенства в другую;
- При различных тождественных преобразованиях, не меняющих смысл равенства;
- При умножении или делении одновременно обеих частей уравнения на один и тот же коэффициент;
Важно понимать, что, осуществляя различные преобразования в уравнении, нельзя искажать область определения какой-либо из переменных. Большинство тождественных преобразований сохраняют неизменным множество х или у, но бывают неприятные исключения. Рассмотрим такой пример:
у = х(2/(х) + 4)
Для решения этого уравнения логичнее было бы раскрыть скобки: совершить вполне тождественное преобразование, которое почти никогда не затрагивает область определения переменных. Но в данном случае раскрытие скобок не будет тождественным явлением. В изначальном варианте представленное уравнение имеет множество решений х, исключая х = 0, так как при данном значении одночлен 2/х потеряет смысл вместе со всем уравнением. Если же мы раскроем скобки, то получим следующее:
у = х(2/(х) + 4) = 2х/х + 4х = 2 + 4х
Как легко заметить, в новом уравнении область определения х является бесконечной, включая х = 0. То есть, множество значений х изменилось, уравнение не является равносильным заданному примеру. Тем не менее, часто подобные упражнения решают обычными преобразованиями. Просто нужно совершать подстановочную проверку, что бы исключить недействительные решения уравнения.
Подавляющее большинство уравнений с двумя переменными преобразуется в аналитические зависимости, после чего совершается подстановка любых двух значений х и вычисляется, таким образом, пара решений х и у. При этом, самих решений, как правило, бесконечное множество. Но есть и небольшие исключения – когда из области определения переменной выпадает какая-либо точка. Некоторые уравнения с двумя неизвестными имеют только одно решение, например, выражение х2 + у2 = 0 имеет только одну пару корня – (0, 0). А уравнение вида х2 + у2 = -1 не имеет действительных решений вообще. То же справедливо по отношению к любым подобным уравнениям, которые равны отрицательным числам – ведь квадраты, как и их суммы, в принципе не могут дать отрицательных значений.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5307 |
| Номер материала | 474 |