
Презентация "Функция y=x^3. Степенная функция с нечетным показателем"

Краткое описание документа:
Начните урок с определение темы, чтобы ученики понимали, что в данном случае речь пойдёт о степенных функциях с нечётным показателем. Вспомните пройденное определение степенной функции, где расположена независимая переменная и степенной показатель. Почему показатель должен быть натуральным числом? Какие свойства были характерны степенной функции с нечётными показателями?


слайды 1-2 (Тема презентации "Функция y=x^3. Степенная функция с нечетным показателем", пример)
Вновь повторите тему и спросите, какие числа являются нечётными и кто может привести пример степенной функции с нечётным показателем. Кроме общих представлений о функции, ученики будут разбираться в характерных свойствах, а также научаться строить график.
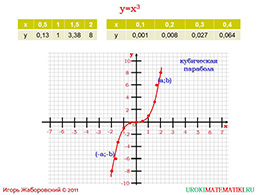
Для начала рассмотрим свойства функции до того, как перешли к графику. Одно из первых свойств - функция равна нулю, если аргумент является нулем. Данное свойство уже встречалось при изучении степенных функций с чётным показателем. Поэтому напишите уравнение «у», равняющееся «х» в кубе при аргументе являющимся нулю и посмотрите, сможет ли кто сказать, чему равняется функция.
Второе свойство – положительность функции при всех значениях. Приведите пример кубичной функции и спросите, может ли ответ быть отрицательным числом. Если правильного варианта не прозвучало, то возведите в куб два, три и четыре. Тогда дети поймут, что число не может быть отрицательным при умножении на самого себя.
Третье и заключающее свойство – противоположное значение аргумента порождает противоположное значение функции. Это главное различие со степенной функцией, у которой показатель чётный. Следовательно, функция является нечётной, то есть «у» от минус «х» равняется минус «у» от «х». Это означает, что график данной функции симметричен относительно начала координат.
слайды 3-4 (примеры)
Далее напишите формат функции и предложите ученикам просчитать значение функции при значении аргумента от нуля до двух (желательно брать половинный интервал для точности просчёта).
Видно, что функция возрастает и не ограничена ни снизу, ни сверху, не имеет ни наибольшего, ни наименьшего значения, то есть она непрерывна, поэтому «у» принимает все значения: от плюс до минус бесконечности. Стоит отметить, что функция является выпуклой. Например, возьмём две точки на отрезке от минус бесконечности до нуля, соединив их, увидим, что кривая будет находиться выше построенной прямой. Если возьмём также две точки, но уже на промежутке от нуля до плюс бесконечности, то построенная прямая будет находиться выше кривой.
Прочтём график: если аргумент возрастает от минус бесконечности до нуля, то функция возрастает от минус бесконечности до нуля. Если «х» равен нулю, то функция равна нулю. Если аргумент возрастает от нуля до плюс бесконечности, то функция возрастает от нуля до плюс бесконечности.
Область определения функции – все «х», от минус до плюс бесконечности. Значит любое значение «х» можно возвести в куб и так получить одну из точек функции.
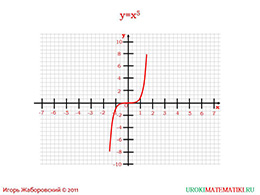
Функции других степенных функций с другим нечётным показателем аналогичны.
Рассмотрим следующую функцию, когда «у» равен «х» в степени пять. Предложите рассчитать ученикам значения функции, используя значение аргумента от нуля до двух с половинчатыми интервалами. Обязательно акцентируйте внимание на использовании калькулятора. По завершению рядом с предыдущей функцией попросите одного из учащихся нарисовать данную. Какие различия между ними видны, и какой вывод можно сделать по значению показателя степени. Для закрепления материала, завершите урок, вспоминая различие степенной функции с чётным и нечётным показателем, перечислением их свойств и различными графиками.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5431 |
| Номер материала | 214 |