
Урок "Функция y=x^2. Степенная функция с четным показателем"

Краткое описание документа:
Изучим формулы для нахождения площади квадрата и объема куба. Согласно геометрическим законам, площадь квадрата равна квадрату его стороны, а объем куба равен кубу его ребра. В линейном виде:
S = а2
V = а3
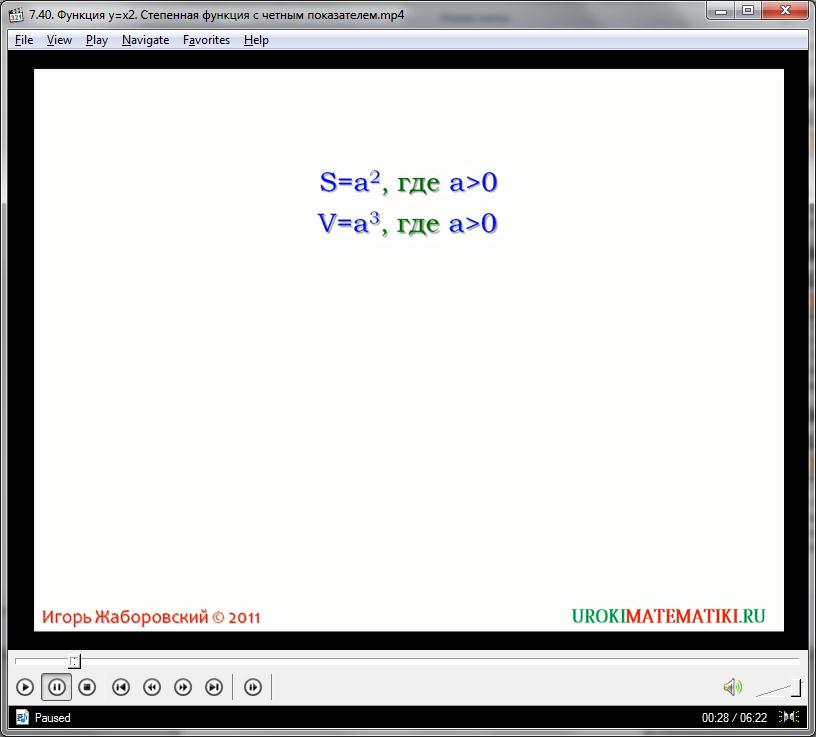
Где а – это, соответственно, сторона квадрата и ребро куба. Легко понять, что данные формулы соответствуют некоторым зависимостям. Действительно, площадь квадрата зависит от значения его стороны, а объем куба зависит от показателя его ребра. Каждая из этих зависимостей формирует функции:
S = f(а)
V = f(а)
В первом случае функция квадратичная, а во втором – кубическая. Мы можем записать эти геометрические формулы в виде абстрактных математических выражений, являющихся линейными аналитическими функциями:
S = f(а) преобразуем в у = а2
V = f(а) преобразуем в у= а3
Любые функции, которые представляют собой зависимость между множеством аргументов, имеющих определенную степень, и множеством соответствующих значений именуются степенными функциями. Общая формула для данного типа зависимостей имеет вид:
у = (х)n
Где n – некая натуральная степень аргумента, являющаяся определителем всего степенного порядка данной функции. Следует заметить, что в частном случае при n = 1, степенная функция вырождается в линейную зависимость:
у = (х)n
у = (х)1 = х
у = х
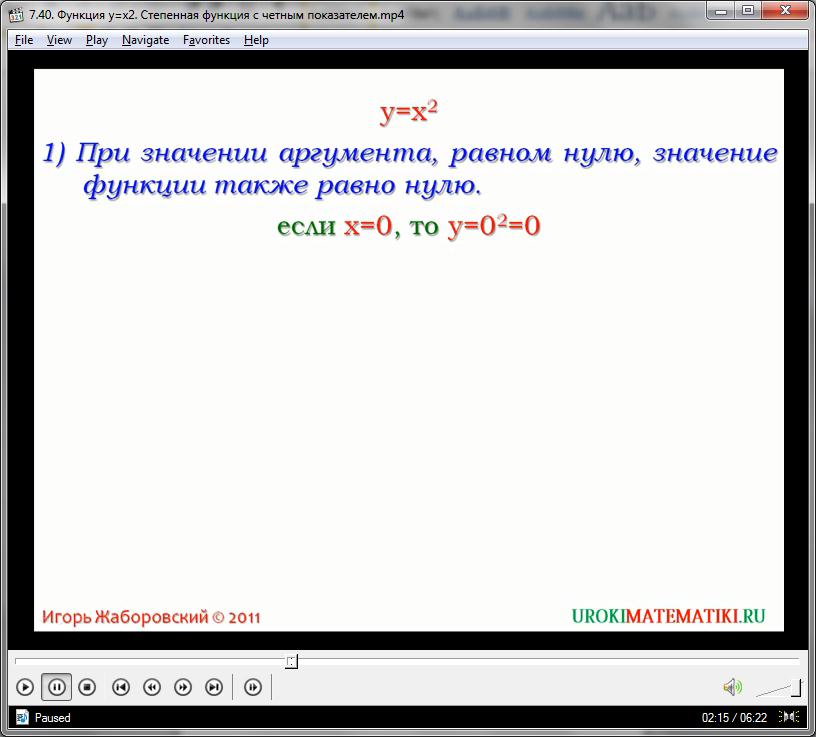
Для того, чтобы лучше передать свойства степенной функции, видеоурок представляет несколько основных тезисов на примере обычной квадратичной зависимости. Предположим, у нас есть функция вида:
у = х2
Это квадратичная зависимость: каждое значение у соответствует квадрату аргумента. График функции проходит через центр координат (0, 0), так как при значении х = 0, функция так же приобретает нулевое значение, то есть точка координат (0, 0) принадлежит графику данной зависимости.
Как известно их видеоуроков, посвященных степеням, возведение в квадрат (или, в общем, четную степень) любого выражения удаляет знак «минус», превращая выражение в полностью положительное. Иначе говоря, не существует квадратов каких-либо чисел, которые имеют отрицательное значение. Из формулы нашей зависимости видно, что при любом, даже отрицательном значении аргумента у всегда будет положителен. Это означает, что область значений функции лежит в положительной части множества чисел, включая также нулевую точку. При этом область определения аргумента распространяется на все числовое множество.
График функции должен пролегать в первой (х, у), или во второй (-х, у) четвертях системы координат.
Квадратичная зависимость выявляет ещё одну закономерность. Подставим в формулу нашей функции как аргумент любую пару одинаковых чисел, имеющих противоположное значение, то есть а и –а:
у = х2
у = (+а)2 = а2
у = (-а)2 = а2
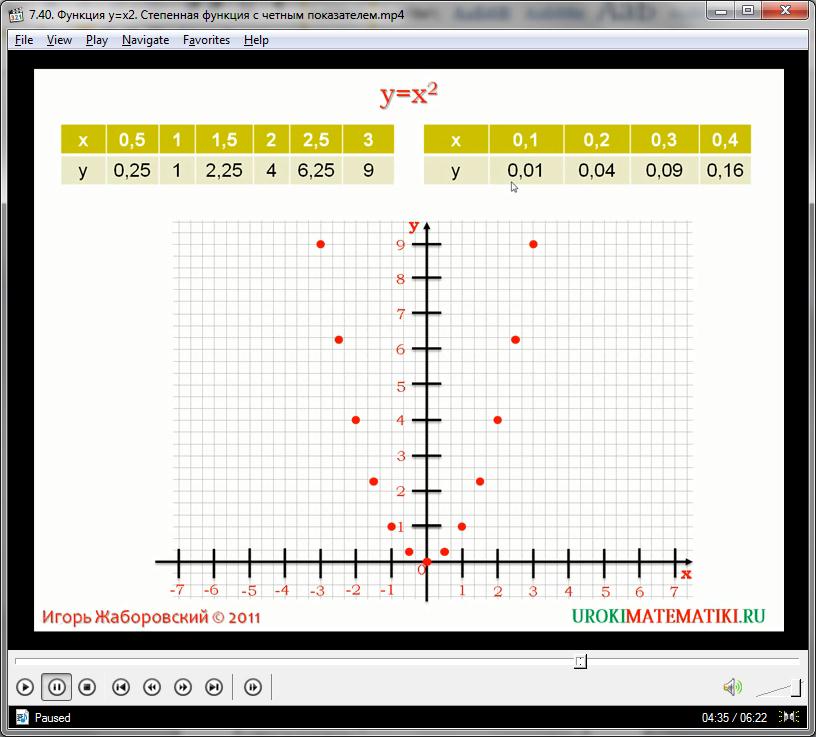
Как мы видим, пара полярных аргументов выдает одинаковое значение функции. Из правил извлечения квадратного корня известно, что любой реальный корень из числа а всегда имеет два значения – это пара одинаковых чисел, имеющих противоположные знаки. Применимо к свойствам квадратичной функции можно выразить так: каждому значению функции у = х2 соответствует пара аргументов х и –х. На графике зависимости это проявляется в симметричности относительно оси ординат. Расчитаем координатную сетку для функции у = х2 в интервале х (-2, у) (2, у):
у = х2
х = -2, у = (-2)2 = 4
х = -1, у = (-1)2 = 1
х = 0, у = (0)2 = 0
х = 1, у = (1)2 = 1
х = 2, у = (2)2 = 4
Построим график при помощи данной таблицы. Квадратичная функция дает возможность визуализировать особую математическую кривую, именуемую параболой. Парабола представляет собой две симметричные кривые, соединенные общей точкой – вершиной. В случае функции у = х2 парабола имеет вершину в центре координат, и ветви, направленные вдоль оси ординат вверх, в бесконечное множество значений у.
Все вышеописанные правила прекрасно работают с любыми четными функциями, то есть для зависимостей вида:
у = (х)n
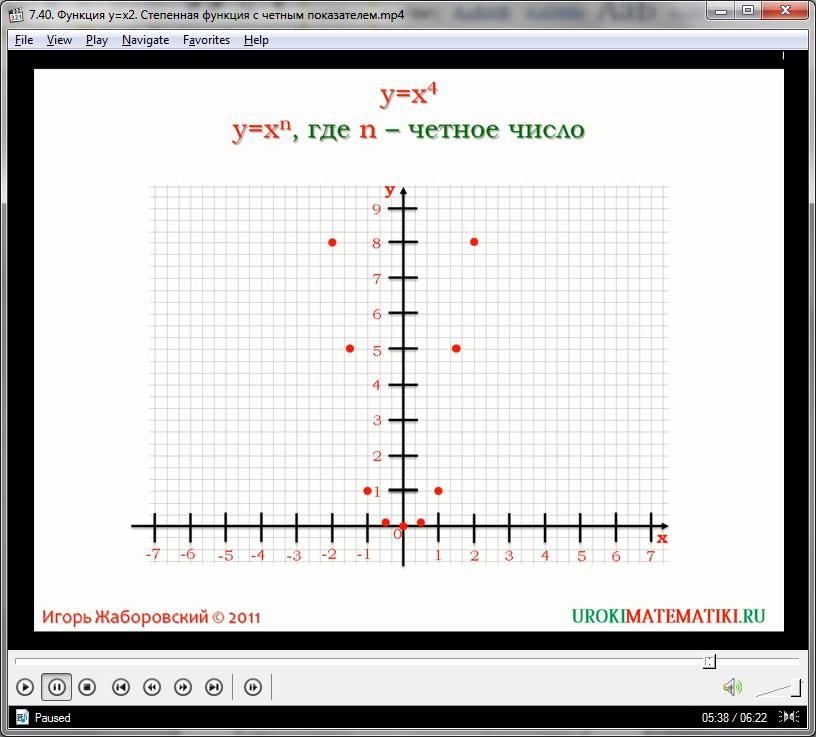
где n – натуральное четное число. Если мы построим график функции четвертой степени:
у = (х)4,
то увидим, что он представлен похожей параболой. Отличие от графика квадратичной функции будет заключаться лишь в том, что парабола четвертой степени имеет более сжатый вид – её ветви тяготеют к оси ординат. Математически можно сказать иначе: даже при сравнительно малых значениях аргумента значение функции очень резко начинает возрастать. Соответственно, чем больше степень функции, тем быстрее будет прирастать значение у, тем более сжатой будет парабола.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8346 |
| Номер материала | 472 |