
Презентация "Система линейных уравнений. Графическое решение системы"

Краткое описание документа:
На данном уроке учащиеся сначала узнают, что такое система уравнений, в чём особенность системы линейных уравнений, а также увидят специфику совокупности их графиков. Это и известно в математике как графический метод решения системы уравнения. Давайте вернёмся к теме уравнения и вспомним, что его решением выступают все возможные значения. В каком-то случае это может быть множество всех значений, а в линейном уравнении - это две точки, через которые проходит прямая.


слайды 1-2 (Тема презентации "Система линейных уравнений. Графическое решение системы", пример)
Повторим линейные уравнения на следующем примере, где сумма «х» и «у» равняется двум. Что тогда будет решением данного уравнения? Получается, парой чисел здесь может быть один и один, минус пять и семь, три и минус один. Более того, ответов будет бесчисленное множество.

слайды 3-4 (примеры)
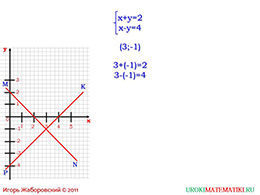
Теперь возьмём систему, где сумма чисел равна двум, а их разность равна четырём. В данном случае мы получаем два линейных уравнения, которые мы объединяем скобкой. Далее стоит дать определение тому, чем является решение системы (решение системы должно обращать каждое уравнение в верное равенство).
Чтобы решить систему линейных уравнений, необходимо найти все пары чисел «х», «у», которые удовлетворяю функции. Удобнее всего изображать функции графически, чтобы видеть эту точку пересечения, которая является решением каждого уравнения. В нашем случае оба уравнения линейные, соответственно графиками функций является прямая. Следовательно, строим график каждой функции и находим точку пересечения. Видим, что точка пересечения имеет координаты три и минус один. Если подставим их в каждое уравнение, то выходит верное равенство, поэтому ответ правильный. Теперь мы видим, что решением системы линейных уравнений является координаты конкретной точки, которая находится на пересечении двух прямых. Соответственно, линейная система получает единственное решение. Если вспомнить специфику линейных систем, то они могут: иметь одно решение, когда прямые пересекаются; не иметь вообще решений, если прямые параллельны; и иметь множество решений, когда прямые совпадают.


слайды 5-6 (примеры)
Теперь сделаем первый относительно самостоятельный пример для учеников. В системе линейных уравнений дана сумма минус тридцати пяти «х» и десяти «у», равная семидесяти восьми, и сумма двадцати одного «х» и пяти «у», равная сорока шести. Сделаем некоторое преобразование, чтобы найти «у» для каждого уравнения. Попросите кого-то из учеников показать решение и проанализировать результат на доске.
Следующий пример учащиеся должны уже более активно обсуждать. В одном уравнении разность четырёх «х» и двух «у» равняется трём, а в другом – разность восьми «х» и четырёх «у» равняется единице. Теперь вовлеките хотя бы двух учеников, спрашивая каждого решение одного уравнения, а третьего можете привлечь, чтобы он проанализировал систему и то, как он выяснил количество решений системы.

слайд 7 (пример)
На полное закрепление предоставьте третий пример, где разность трёх «х» и двух «у» равна четырём, а сумма минус четырёх с половиной «х» и трёх «у» равно минус шести. Повторите задание учащимся: необходимо найти количество решений для системы. В итоге вы должны услышать, что этот пример отличается от предыдущих двух, потому что имеет лишь одно решение.
Мы рассмотрели частные случаи общей системы, поняли, что решением системы линейных уравнений является пара чисел, которая делает каждое уравнение верным неравенством. На графике эта пара чисел выступает координатами точки, которая находится на пересечении. Стоит не забывать, что функция убывает, когда угловой коэффициент перед переменной отрицательный.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3827 |
| Номер материала | 218 |