
Урок "Решение линейных уравнений с двумя переменными в целых числах"

Краткое описание документа:
Прошлый видеоматериал был посвящен линейным уравнениям, содержащим две переменные. Мы рассмотрели основные свойства подобных выражений, возможности их преобразования и решения, а также графическое отображение зависимости между двумя переменными.
Известно, что подавляющее большинство этих уравнений имеют множество ответов, представленных всегда парой чисел. Эта пара – значения х и у. Рассмотрим возможные варианты корней уравнения следующего вида:
5х – 3у = 2
Очевидно, что корнями данного уравнения может быть пара (4, 6):
5(4) – 3(6) = 2
Или же дроби 1/5 и 1/3:
5(1/5) – 3(1/3) = 2
В обеих случаях получается верное равенство, значит обе пары корней приемлемы в качестве решения представляемого уравнения. Но при этом одна пара является дробями, а вторая представлена целыми числами. Корни уравнений с двумя переменными, имеющие значения в целых числах именуются цельно численными.
Довольно часто в математике встречаются задачи, требующие именно целочисленные решения подобных уравнений. С другой стороны, некоторые вариации, вроде:
2х + 3у = 1/5
Не имеют цельно численных решений вообще. Так как при любых целых значениях х и у получится целое общее выражение левой части (2х + 3у), которое никак не может быть равно дроби – то есть, нарушится принцип сохранения равенства.
Рассмотрим возможные решения уравнения:
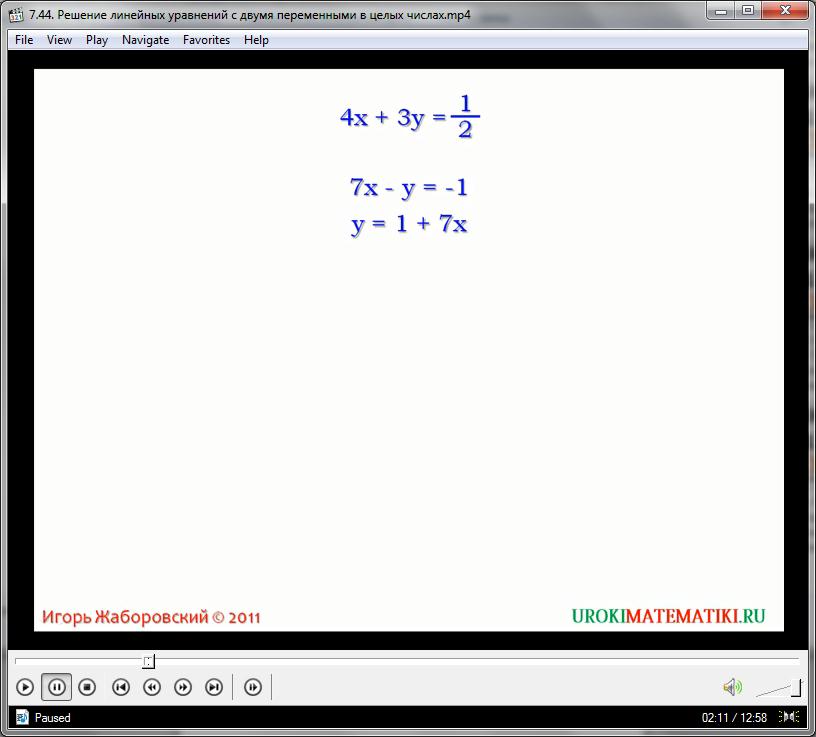
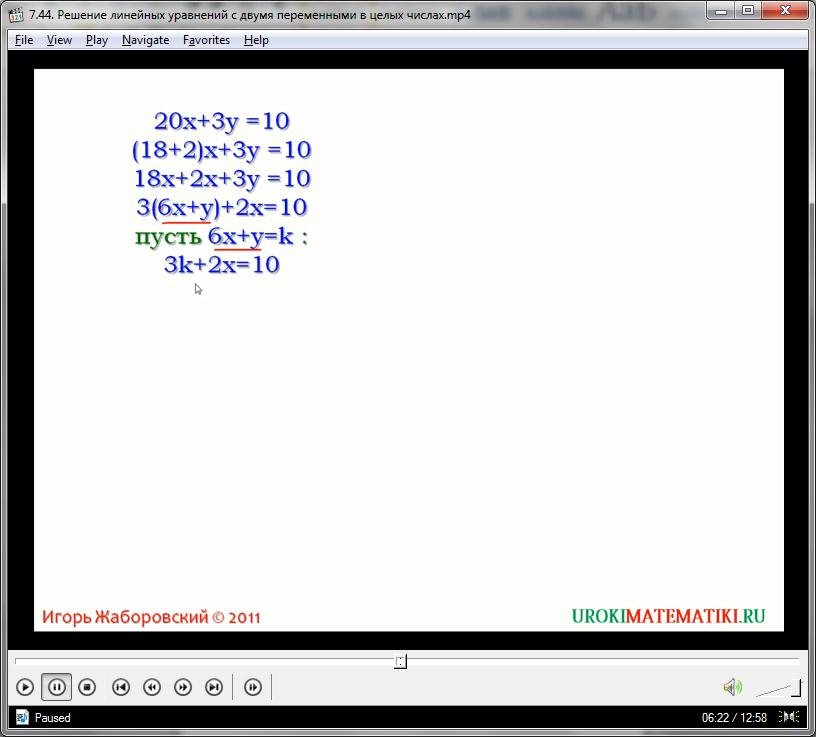
7х – у = -1
Переведем его в форму зависимости, используя перенос через знак равенства и тождественные преобразования:
7х – у = -1
- у = -7х – 1
у = 7х + 1
Вполне очевидно, что сохраняется равенство вида:
у = 7х + 1
х = n
y = 7n + 1
Где n – любое натуральное число, которое вполне может быть целым по значению. То есть, уравнение 7х – у = -1 обладает множеством целочисленных решений. Проверим любые целые числа в качестве х:
у = 7х + 1
х = 2; у = 15
х = 5; у = 36
х = 0; у = 1
х = -3; у = -26
Нам уже известна общая абстрактная формула для определения любого линейного уравнения с двумя переменными:
ax + by = c
Где х и у – переменные, а и b – коэффициенты при переменных, а с – свободный член. Любое уравнение, подобное линейным выражениям с х и у, путем равносильных преобразований можно привести к такому абстрактному виду. Подробное изучение общей формулы позволяет с легкостью выявить некоторые закономерности с точки зрения наличия целочисленных решений. Итак, если задано некое уравнение вида:
ax + by = c
При котором свободный член является дробью, то корнями уравнения никак не могут быть цельно численные выражения. Сумма или разность двух целых чисел по закону элементарной алгебры не может быть равна дробному выражению.
Из-за большого количества возможных решений, корни уравнений с двумя переменными иногда имеют вид не пары отдельных чисел, а пары двух индивидуальных формул – для х, и для у. Для примера, решим уравнение:
20х + 3у = 10
Для этого, нам необходимо совершить ряд преобразований. Разобьем одночлен 20х на тождественную сумму 18х + 2х:
20х + 3у = 10
20х = 18х+ 2х
18х + 2х + 3у = 10
Группируем одночлены, имеющие кратные числовые коэффициенты. Стоит отметить, что переменную х необходимо разбивать на сумму так, что бы получился х с коэффициентом максимально большим и кратным при этом для числового коэффициента переменной у. Так как в нашем примере при у стоит тройка, то х мы разбиваем с максимально допустимым коэффициентом, кратным трем. После группировки выносим общий кратный множитель:
18х + 2х + 3у = 10
18х + 3у + 2х = 10
3(6х + у) + 2х = 10
Пусть выражение в скобках (6х + у) равно некой переменной с, тогда:
3(6х + у) + 2х = 10
(6х + у) = с
3с + 2х =10
Разбиваем значение переменной с по такому же принципу, как разбивали коэффициент при х. При этом нам необходимо подобрать некое число, которое будет кратно двойке (значению при 2х), но не больше трех. Очевидно, что это будет так:
3с + 2х =10
3с = 2с + с
2с + с + 2х =10
Проводим тождественные изменения:
2с + с + 2х =10
2(с + х) + с = 10
Обозначим содержимое скобок, как n, тогда:
2(с + х) + с = 10
(с + х) = n
2n + с = 10
с = 10 – 2n
Подставляем получившееся равенство вместо с:
3с + 2х =10
с = 10 – 2n
3(10 – 2n) + 2х = 10
И решаем полученное уравнение относительно переменной х:
3(10 – 2n) + 2х = 10
30 – 6n + 2х = 10
2х = 10 + 6n – 30
х = - 10 + 3n
Так как:
(6х + у) = с
(с + х) = n
с = n – х
То уместно записать:
6х + у = n – х
Подставляем известную нам формулу для х, что бы вычислить у:
6х + у = n – х
х = - 10 + 3n
6(- 10 + 3n) + у = n – (- 10 + 3n)
-60 + 18n + у = n + 10 - 3n
у = n + 10 - 3n + 60 – 18n
у = 70 - 20n
Корнями уравнения 20х + 3у = 10 являются два выражения вида:
х = - 10 + 3n
у = 70 - 20n
Где n – любое целое число – 0, 1, 2 и т.д. Таким образом, чтобы описать все многообразие возможных целочисленных решений, проще всего вычислить некоторые формулы для быстрого расчета х и у. Подставляя любые выражения n в эти формулы, можно с легкостью получить искомую пару чисел.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 11580 |
| Номер материала | 476 |