
Презентация "Способ подстановки"

Краткое описание документа:
В этот раз учащиеся познакомятся с наиболее популярным методом решения систем уравнений (как линейных, так и нелинейных). Для линейных систем способ подстановки, которые мы сегодня изучаем, является наиболее распространённым. Теперь важно сформулировать суть способа и рассмотреть несколько примеров для того, чтобы его эффективно применять.

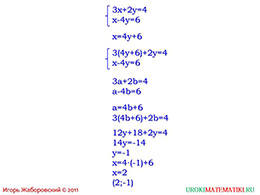
слайды 1-2 (Тема презентации "Способ подстановки", пример)
Рассмотрим пример, где линейная система с двумя неизвестными переменными «х» и «у». Требуется её решить, а это мы можем сделать именно с помощью данного метода. Удобно из второго уравнения выразить «х» через «у», так как коэффициент перед «х» является единицей. Теперь полученное значение «х» подставляем в верхнее уравнение вместо «у». Введём вместо значения «х» новую переменную «а», а вместо «у» переменную «b». Полученные линейные уравнения решаем до конца, выражая «а». В результате мы находим значение данной системы, которое является точкой с координатами два и минус один.


слайды 3-4 (алгоритм решения системы двух линейных уравнений способом подстановки, примеры)
Теперь стоит подробнее остановиться на способе подстановки, который имеет следующий процесс:
- Изначально происходит работа над одним уравнением, относительно определённой переменной. Переменная должна иметь наименьший коэффициент (в идеале – один или посмотрите внимательно, нельзя ли разделить всё уравнение на какой-то число);
- Далее полученное выражение подставляем в исходное уравнение вместо переменной;
- Теперь уравнение имеет лишь одну переменную и его можно легко решить;
- Когда найдена одна переменная, её значение подставляется к другой.
Данный метод позволяет свести решение системы к решению одного уравнения с одним неизвестным. Специфика линейных систем: она может иметь одно решение (когда прямые пересекаются), множество решений (когда прямые совпадают) и не иметь решений вовсе (когда прямые параллельны). Именно метод подстановки позволяет выловить и показать количество решений.
Рассмотрим пример, где дана линейная система. В первом уравнении разница пяти «х» и двух «у» равна шестнадцати, а во втором – разница десяти «х» и трёх «у» равна двадцати семи. Здесь появляется определённая сложность: нет переменной, где есть коэффициент единица. Тогда стоит выбрать переменную с наименьшим коэффициентом (в нашем случае – два). В первом уравнении выражаем «у» через «х», переносим минус в правую часть и избавляем от коэффициента, разделив всё на два. После этого в исходное уравнение подставляем полученное значение «у». Для того чтобы решить уравнение наиболее удобным способом и избавиться от знаменателя, необходимо умножить уравнение на два. Раскрыв все скобки и сделав все преобразования (привели подобные члены), мы получаем, что «х» равняется одной целой две десятых, а «у» - минус пяти.

слайд 5 (пример)
Второй пример должен быть закрепляющим для учащихся. Однако кто сумеет разгадать определённую сложность: второе уравнение имеет дробные числа, что же делать? Необходимо перемножить знаменатели, а свободный член на их произведение. В таком случае уравнение будет легче преобразовывать. В итоге оба уравнения имеют коэффициенты при переменных, поэтому в первом уравнении выразим «х» через «у». После этого подставляем полученное значение в исходное уравнение и находим, чему равна переменная «у» (в нашем случае ответ – три). Заключающий этап – найти значение второй переменной. В итоге решением нашей системы является точка с координатами три и два.
Для решения второго примера вызовите несколько учеников к доске, чтобы они могли поэтапно решать систему, анализируя собственные шаги. Последнего человека после записи результата попросите сделать проверку для каждого уравнения. Таким образом, учащиеся наиболее эффективно познакомятся с одним из методов решения систем уравнений.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5828 |
| Номер материала | 219 |