
Урок "Система линейных уравнений. Графическое решение системы"

Краткое описание документа:
Во многих случаях, особенно связанных с решением практических задач, приходится сталкиваться с такой математической конструкцией, как система уравнений. В таких случаях задача базируется на заданных двух переменных, участвующих в построении двух равенств. В новом видеоуроке подробно изучим подобную систему.
Предположим, у нас есть такое упражнение. Сумма двух неизвестных чисел равна двум. Чему равны эти числа? Алгебраически, условие задачи легко отображается линейным уравнением с двумя переменными:
х + у = 2
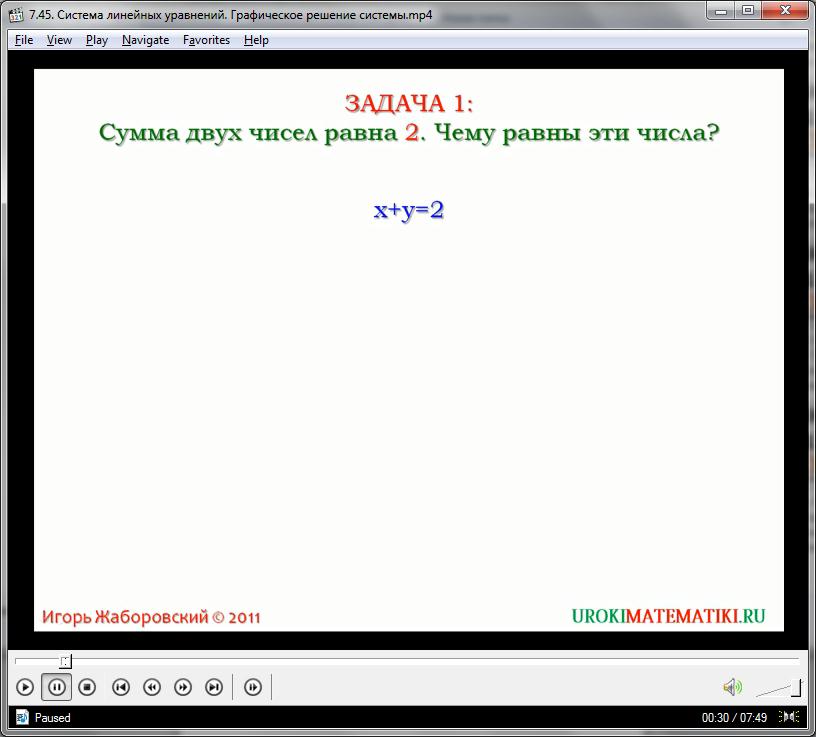
Данное уравнение имеет бесконечное множество решений. Напомним, что ответом, в данном случае, всегда будет пара неких чисел, представляющих собой взаимосвязанные значения х и у. Чтобы сократить количество корней уравнения, зададим ещё одно условие. Пусть наши числа не только дают сумму, равную двум, но и разность, равную четырем:
х – у = 4
При этом стоит обратить внимание, что значения каждой из переменных строго коррелируют между уравнениями, то есть, ответ для них будет общим. Такая пара уравнений, имеющая две переменные и общую пару значений, являющихся ответом, называется системой линейных уравнений:
х + у = 2
х – у = 4
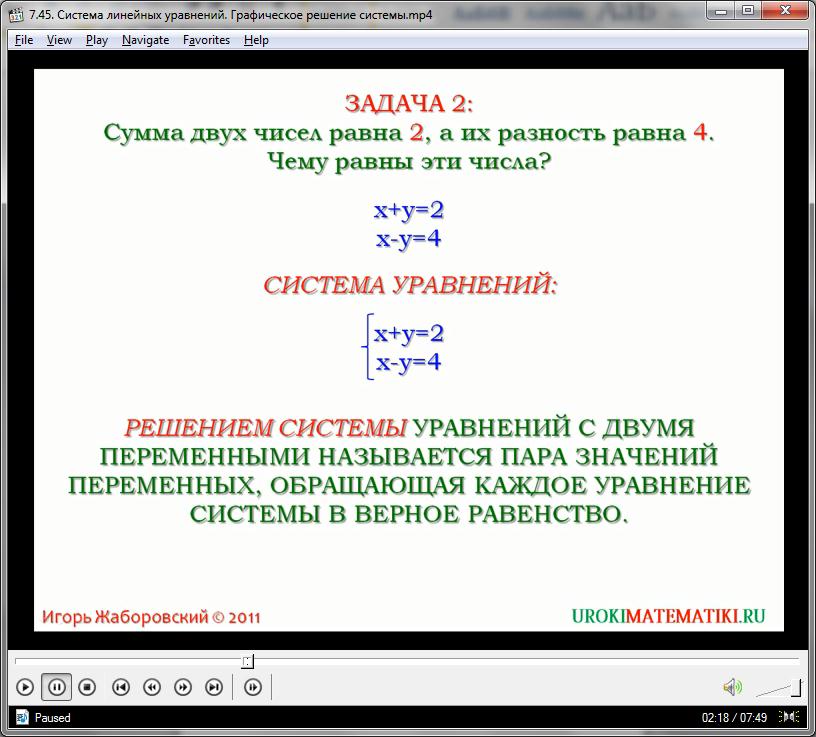
На письме сбоку от пары уравнений записывается обобщающая фигурная скобка. Важно понимать, что пара значений х и у в ответе должна преобразовывать в правильное равенство и первое, и второе уравнения, иначе она не будет являться корректным корнем для этой системы.
Системы линейных уравнений имеют несколько основных способов решения. В данном случае, в нашем видеоуроке мы разберем графический метод. Для этого преобразуем систему в набор функций (или зависимостей) при помощи тождественных равносильных преобразований:
х + у = 2
х – у = 4
у = 2 – х
у = х – 4
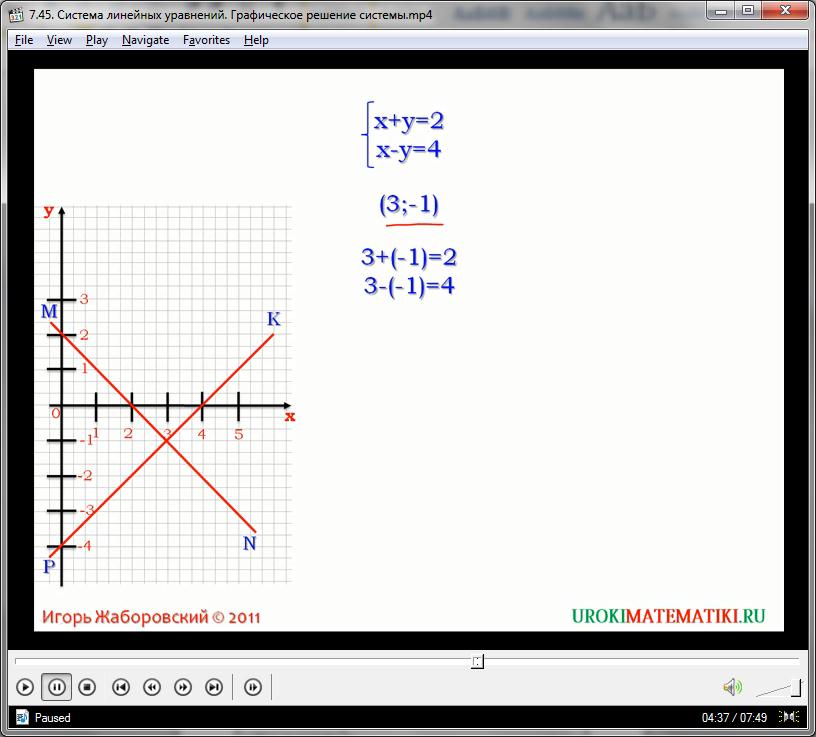
Наши функции являются простейшими случаями прямолинейной зависимости. Графики для них строятся довольно легко на основании двух любых точек, которые рассчитываются в координационной сетке. Итак, построив графики для обеих определенных зависимостей, мы увидим, что это прямые, которые не проходят через центр координат, но при этом, однократно пересекаются друг с другом. Точка пересечения имеет координаты (3, -1). Подставим аргумент и значение зависимости в нашу систему уравнений, вместо х и у соответственно:
3 + (-1) = 2
3 – (-1) = 4
Образовались верные равенства, а значит, пара 3, -1 удовлетворяет систему уравнений, как пара корней. Таким образом, для того, чтобы решить подобную систему, необходимо совершить такой алгоритм действий:
1. Преобразовать уравнения в линейные зависимости, использовав тождественные изменения;
2. Составить координационную сетку хотя бы для двух точек каждого из двух графиков;
3. Отобразить в декартовой системе координат графики обеих зависимостей;
4. Найти точку пересечения графиков (если она есть), и записать её координаты как корни системы уравнений, где аргумент – это х, а значение зависимости – это у.
Следует понимать, что каждое отдельное уравнение с двумя переменными – это линейная зависимость, которую можно отобразить на графике. Она показывает множество связей между парами х и у. И если по самому определению для системы уравнений нужна одно общее решение, то логично искать такие значения х и у, которые будут одновременно соответствовать обоим графикам зависимости.
Особенности пересечения графиков отображают, помимо того, диапазон возможных вариантов решения системы уравнений. При наличии одной точки пересечения (как в случае с двумя прямыми) – решение системы лишь одно, и оно соответствует этой точке. Если пересечений нет – значит, система уравнений не имеет решений вообще (так как при этом не существует общих элементов в двух парах множества). Ну а если прямые совпадают и пересечение вырождается в сливание – ответами на подобную систему будет бесконечное множество чисел, так как любая прямая охватывает бесконечность.
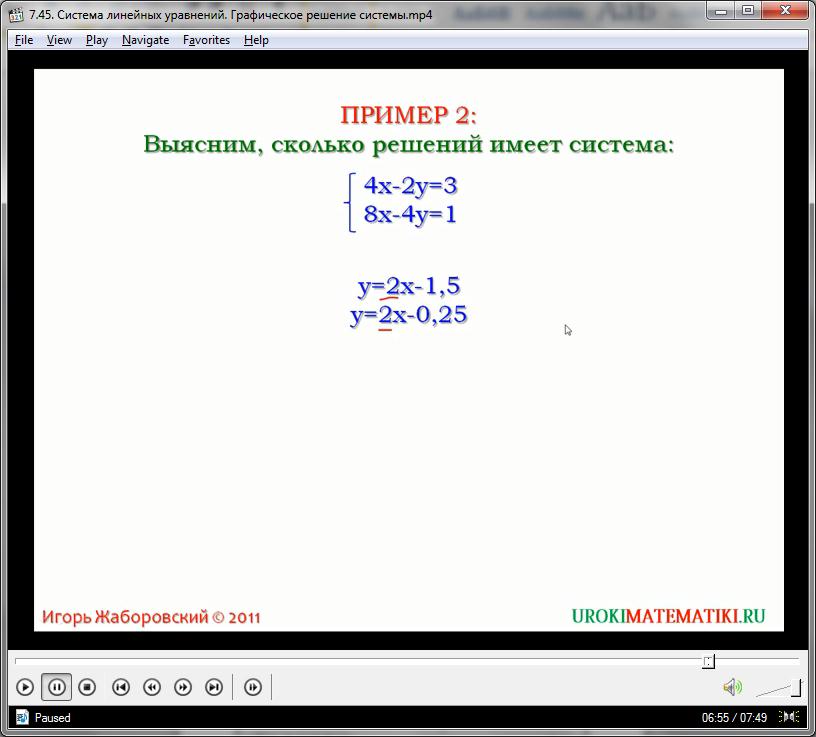
Иногда можно определить наличие корней только лишь по анализу самих уравнений, без применения построения графиков. Рассмотрим пример:
4х – 2у = 3
8х – 4у = 1
Преобразуем уравнения так, чтобы вывести линейные зависимости, использовав тождественные преобразования:
у = 2х – 1,5
у = 2х – 0,25
Из свойств прямолинейной функции известно, что угол наклона прямой в графике зависит от коэффициента при х, а второе слагаемое лишь сдвигает прямую в сторону параллельным переносом. Анализируя наш набор зависимостей, видим, что коэффициенты при х равны, а значит и прямые их графиков имеют одинаковый угол наклона. При этом слагаемые уравнений разные по значению, то есть графики сдвинуты относительно друг друга. Иными словами, прямые параллельны и не пересекаются, значит, данная система уравнений не имеет верных корней.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5523 |
| Номер материала | 477 |