
Презентация урока алгебры в 9 классе на тему "Итоговое повторение по теме "Функции и графики""










![Найдите область определения и значений функции 5 ( -1;5] -3 4 [ -3;4) а) б) в... Найдите область определения и значений функции 5 ( -1;5] -3 4 [ -3;4) а) б) в...](https://fs02.urokimatematiki.ru/e/000231-00f.jpg)


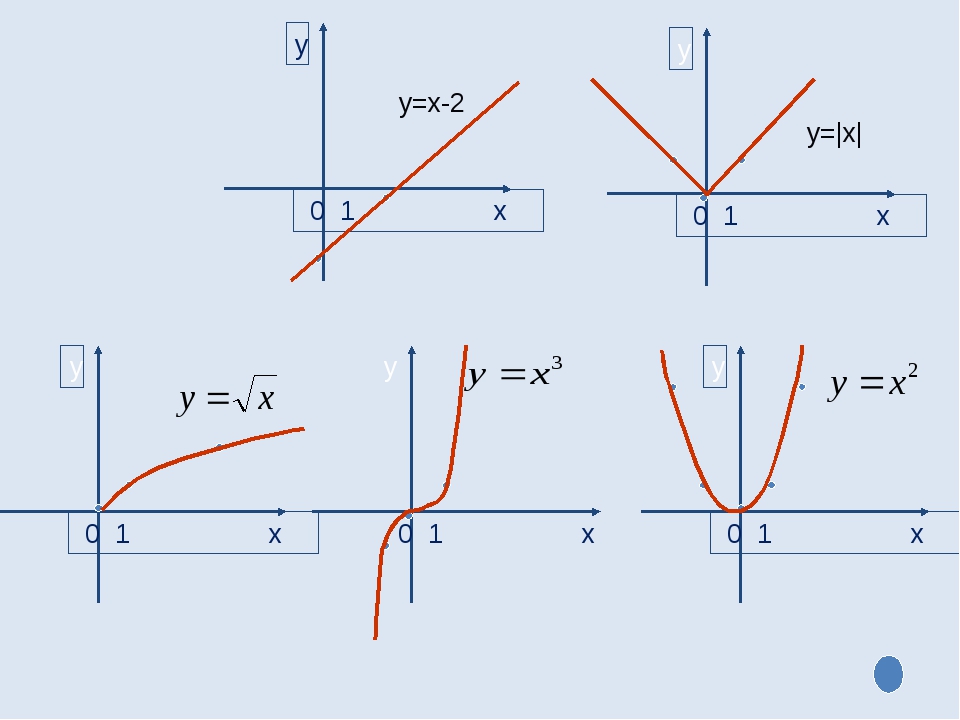












Описание презентации по отдельным слайдам:
Функция – это одно из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами. Слово «функция» (от латинского functio – совершение, выполнение). Лейбниц употреблял это слово с 1673 г. Как термин «функция от x» стало употребляться впервые в 1718 г. одним из учеников и сотрудников Лейбница, выдающимся швейцарским математиком Бернулли Готфрид Вильгельм фон Лейбниц Дании́л Берну́лли
Один из самых замечательных математиков Леонард Эйлер (1707 – 1783), вводя понятие функции, говорил, что «когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых». В формировании современного понимания функциональной зависимости приняли участие многие крупные математики. Описание функции, почти совпадающее с современным, встречается уже в учебниках математики начала XIX в. Активным сторонником такого понимания функции был Н.И. Лобачевский. леонард эйлер Николай Иванович Лобачевский (1792-1856)
«Когда математика стала изучать переменные величины и функции, как только она научилась описывать процессы, движение, так она стала необходима всем». Ф.Энгельс
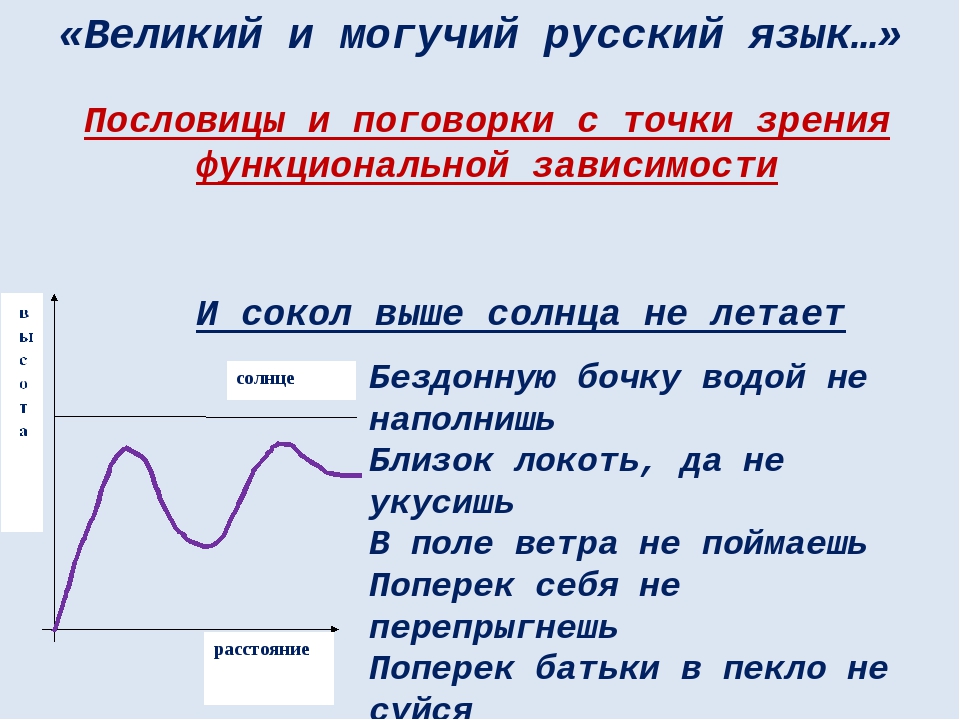
«Великий и могучий русский язык…» И сокол выше солнца не летает Бездонную бочку водой не наполнишь Близок локоть, да не укусишь В поле ветра не поймаешь Поперек себя не перепрыгнешь Поперек батьки в пекло не суйся Пословицы и поговорки с точки зрения функциональной зависимости
«Великий и могучий русский язык…» Кто много знает, с того много и спрашивается Каков строитель, такова и обитель К чему ребенка приучишь, то от него и получишь Кто много читает, тот много знает Как аукнется, так и откликнется Аппетит приходит во время еды С плохими косцами плох и укос Меньше говори, больше делай Работает – как ребенок, а ест – как детина В умной беседе ума набраться, а в глупой свой растерять Худой мир лучше доброй войны Тише едешь – дальше будешь Не все то золото, что блестит Прямая зависимость Обратная зависимость
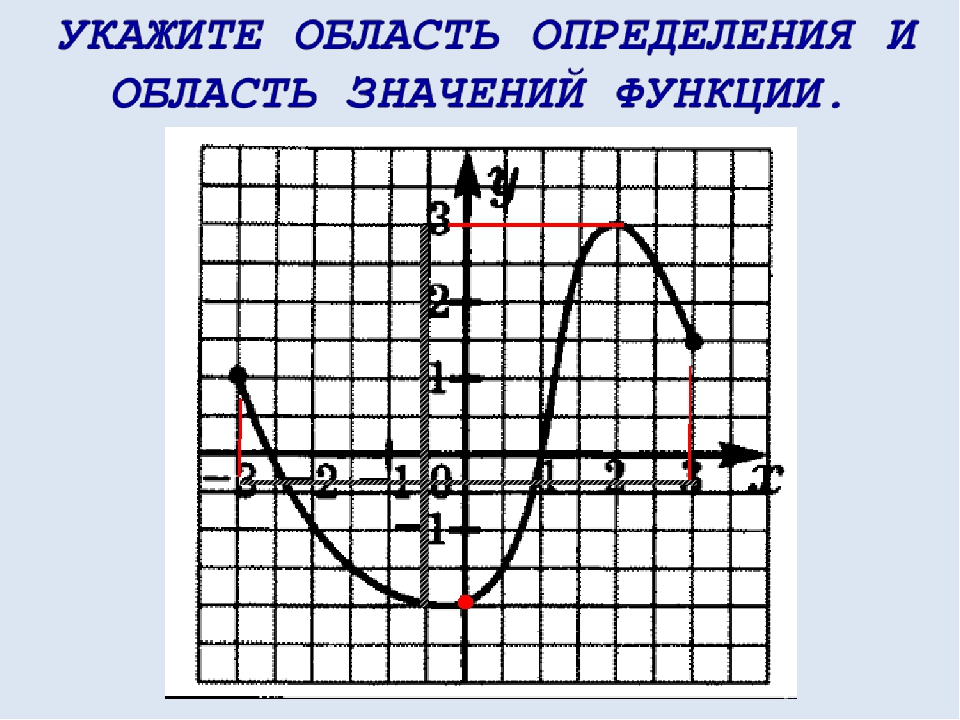
Область определения функции Областью определения функции называют множество всех значений, которые может принимать ее аргумент (х) D(х) Все действительные числа Все действительные числа Х+1≠0 ⇒ Х≠-1 2х-6≥0 ⇒ 2х≥6 ⇒ х≥3 или│3;+∞)
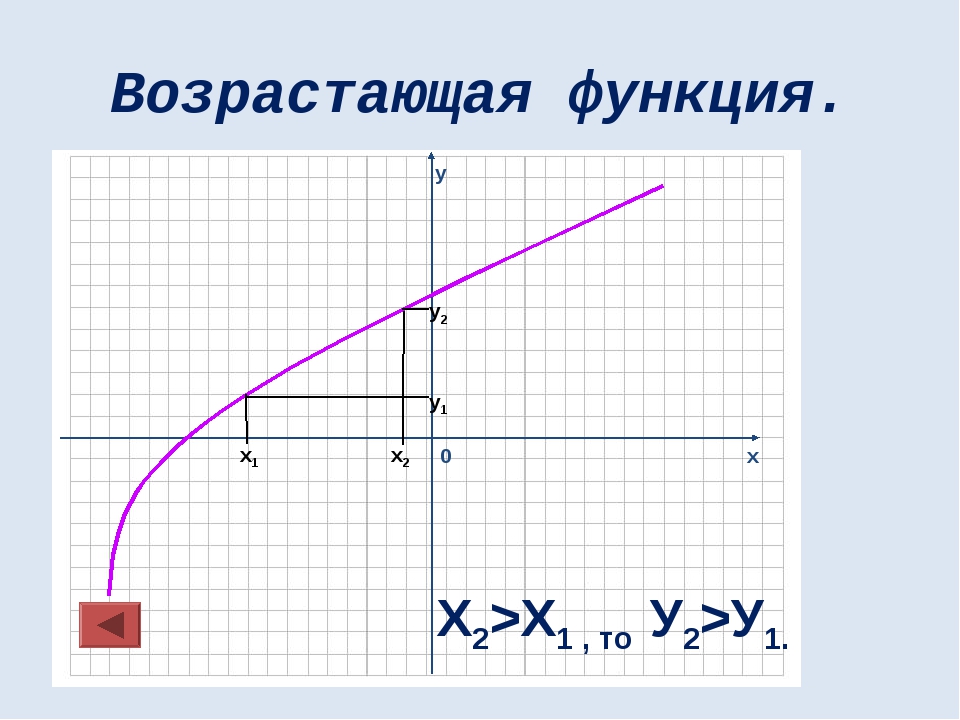
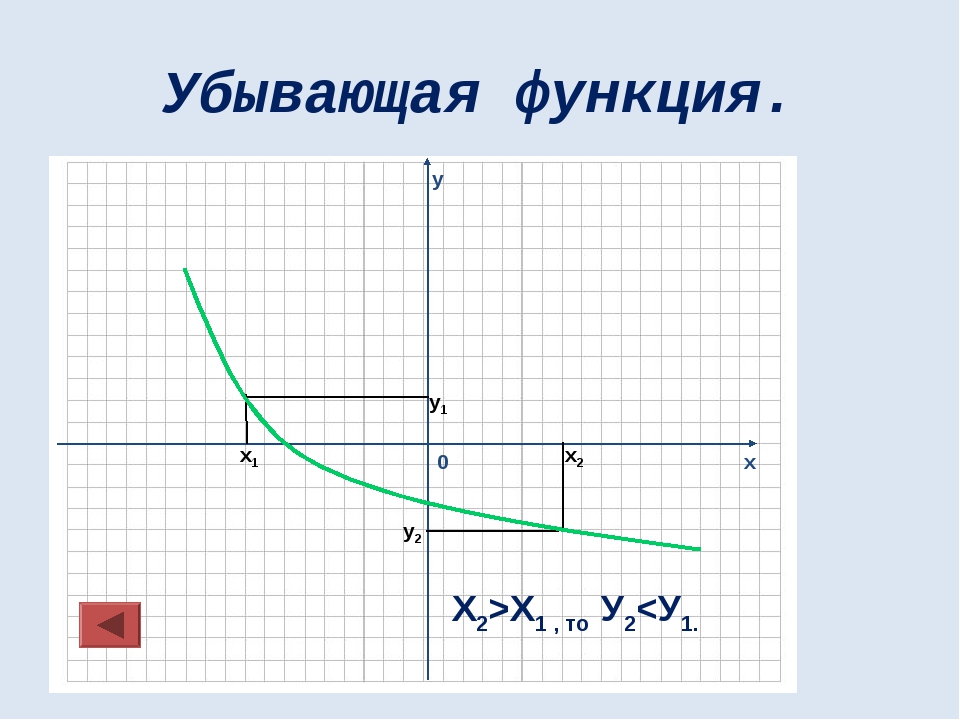
Множество значений функции Множеством значений функции называют множество всех значений которые может принимать переменная у Е(у) Все действительные числа у≥0 у≠0 у≥0
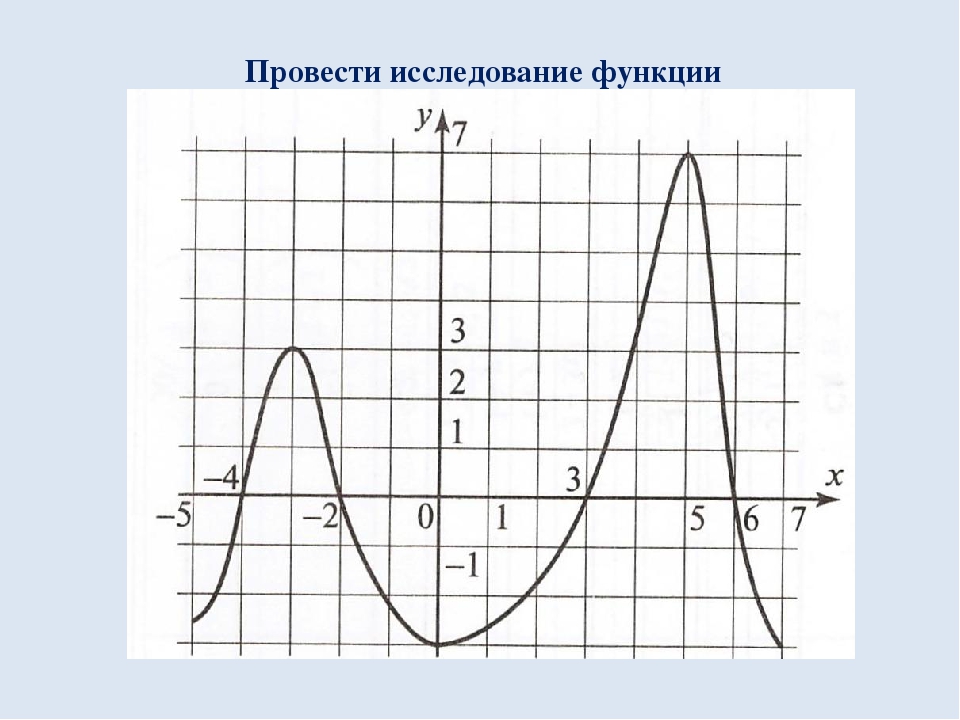
Промежутки, в которых функция сохраняет знак, называют промежутками знакопостоянства У>0 при X∈ (-3; 7); У<0 при X ∈ (-5;-3) ∪ (7;9) У=0 при X=-3 и X=7
Способы задания функции: 4. Словесный 2. Табличный 3. Графический 1. Формулой (аналитический) у=2х+3 х -1 0 1 2 3 у 1 0 1 4 9
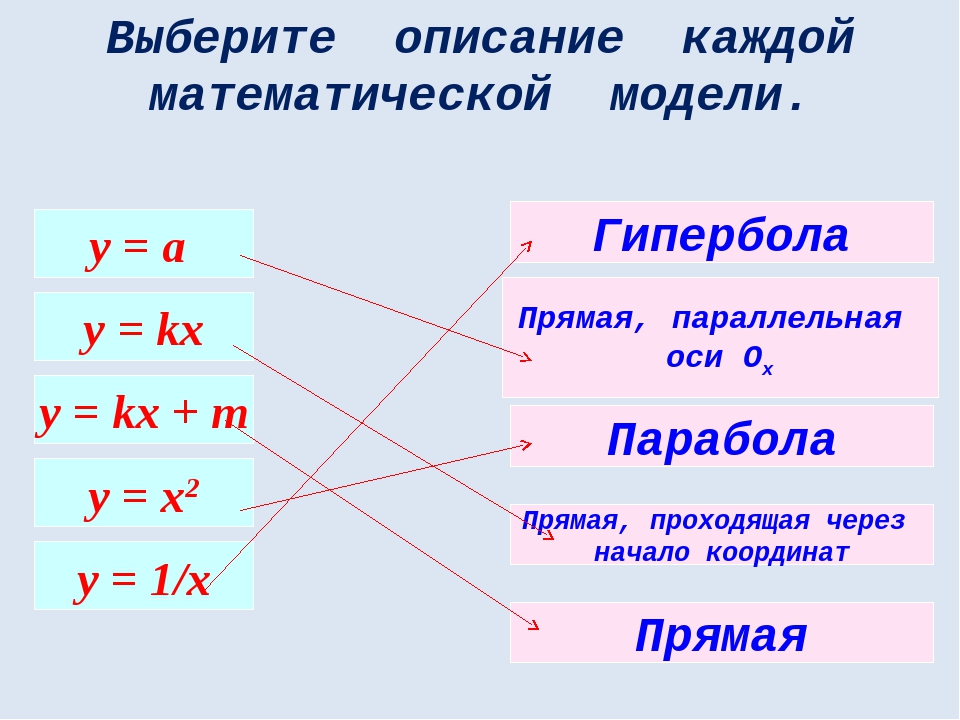
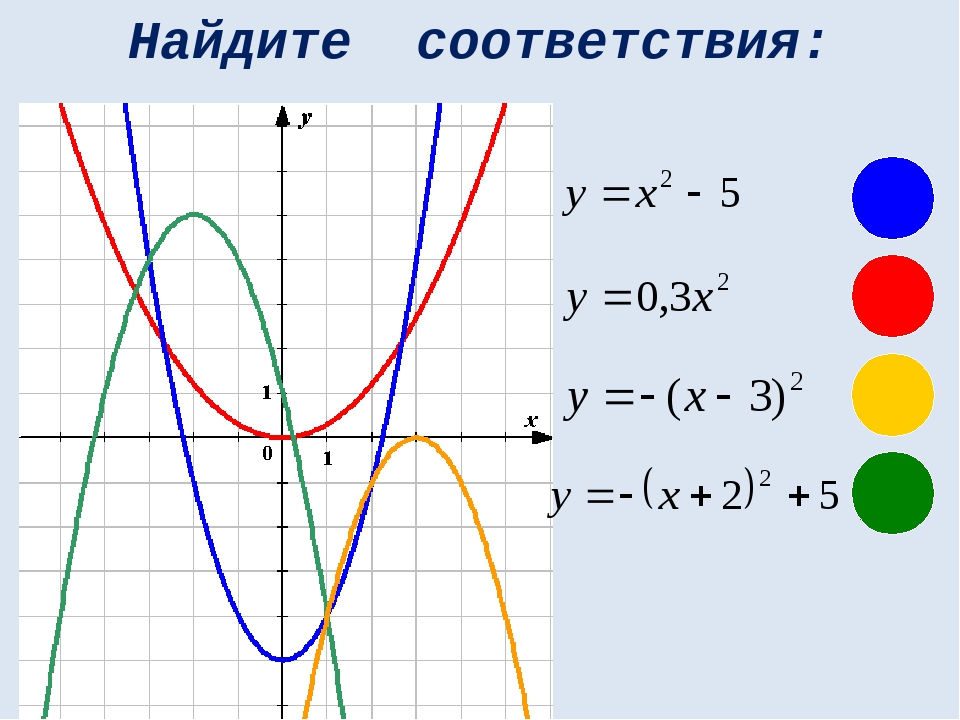
у = а y = kx y = kx + m y = x2 y = 1/x Прямая, параллельная оси Ох Парабола Гипербола Прямая, проходящая через начало координат Прямая Выберите описание каждой математической модели.
Алгоритм построения графика функции у = ах2 + bх +с. 1. Определить направление ветвей параболы. 2. Провести ось симметрии. 3. 4. Определить точки пересечения графика функции с осью Ох, т.е. найти нули функции. 5. Составить таблицу значений функции с учетом оси симметрии параболы. (Найти дополнительные точки) Найти координаты вершины параболы (m; n). Найти точки пересечения графика функции с осью Оу, подставив в y = ax2+bx+c х=0 6.
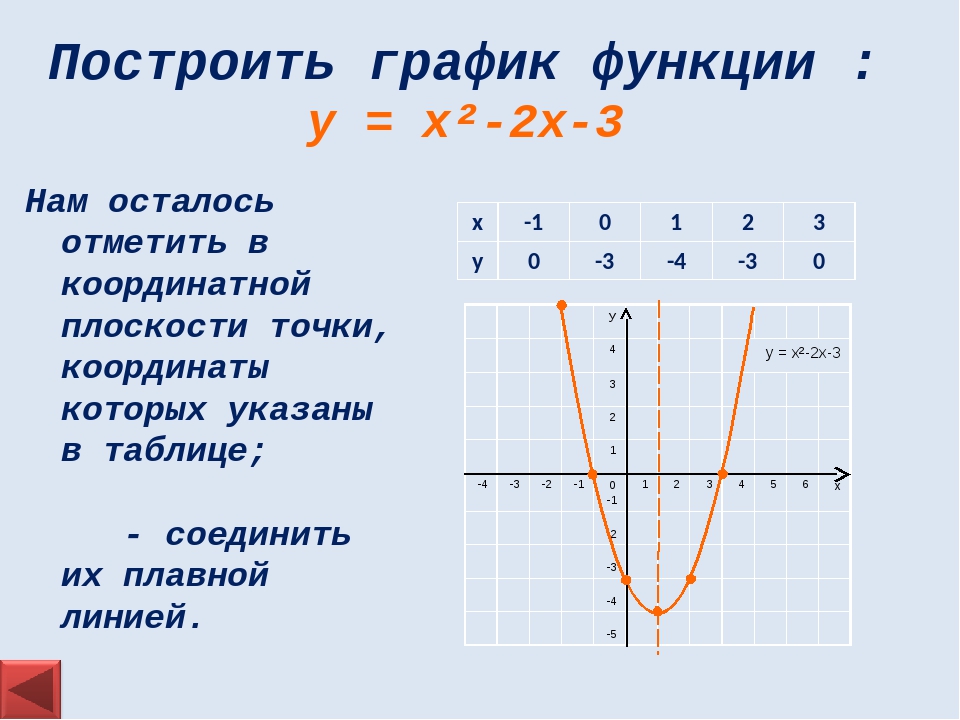
Построить график функции : у = х²-2х-3 у = х²-2х-3 – квадратичная функция, графиком является парабола. 1. Ветви направлены вверх (т.к. а=1, а>0) 2. х=1 – ось симметрии параболы. 3. (а = 1; b = -2; с = -3) Найдём координаты вершины параболы n = 1²-2·1-3 = -4 А(1;-4) – вершина параболы. 4. у=0, х²-2х-3 =0 при х=3 и х=-2; 5. х=0, при у=-3
Построить график функции : у = х²-2х-3 Нам осталось отметить в координатной плоскости точки, координаты которых указаны в таблице; - соединить их плавной линией. У 4 у = х²-2х-3 3 2 1 -4 -3 -2 -1 0 -1 1 2 3 4 5 6 х -2 -3 -4 -5 х -1 0 1 2 3 у 0 -3 -4 -3 0
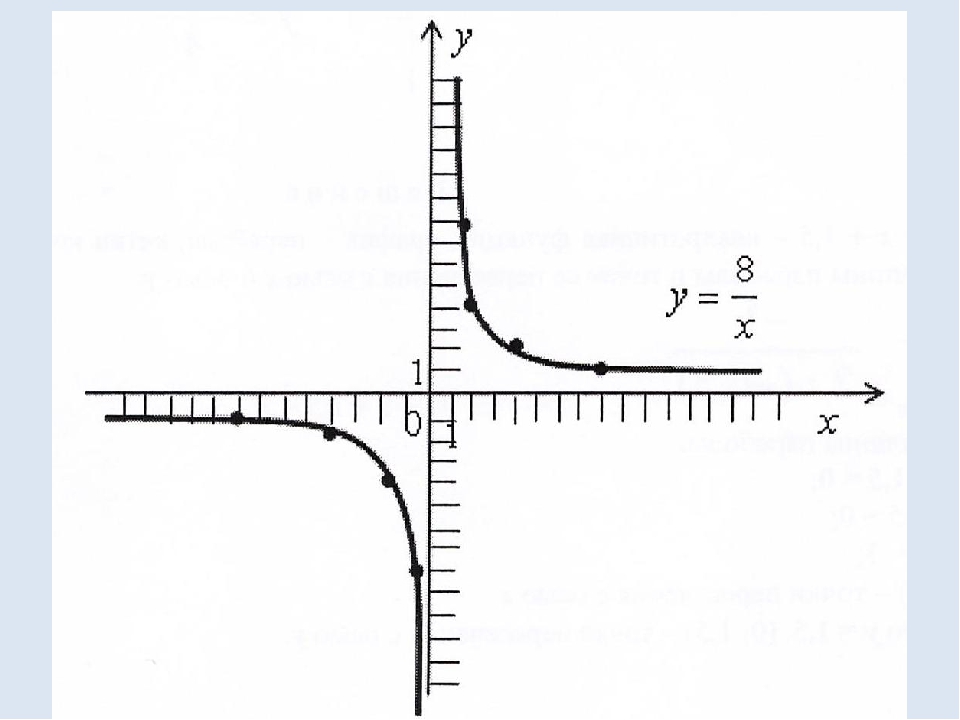
Учебник № 1030(а). Построить график функции у=8/х 1.Это график обратной пропорциональности, к>0 – ветви графика расположены в I и III координатных четвертях. 2.Составим таблицу значений для х>0 3.Вторую ветвь получаем «отражением» относительно начала координат
ОГЭ. Математика : типовые экзаменационные варианты (из сборника под ред. И. В. Ященко. — М. : Издательство «Национальное образование», 2016. — 240 с.)
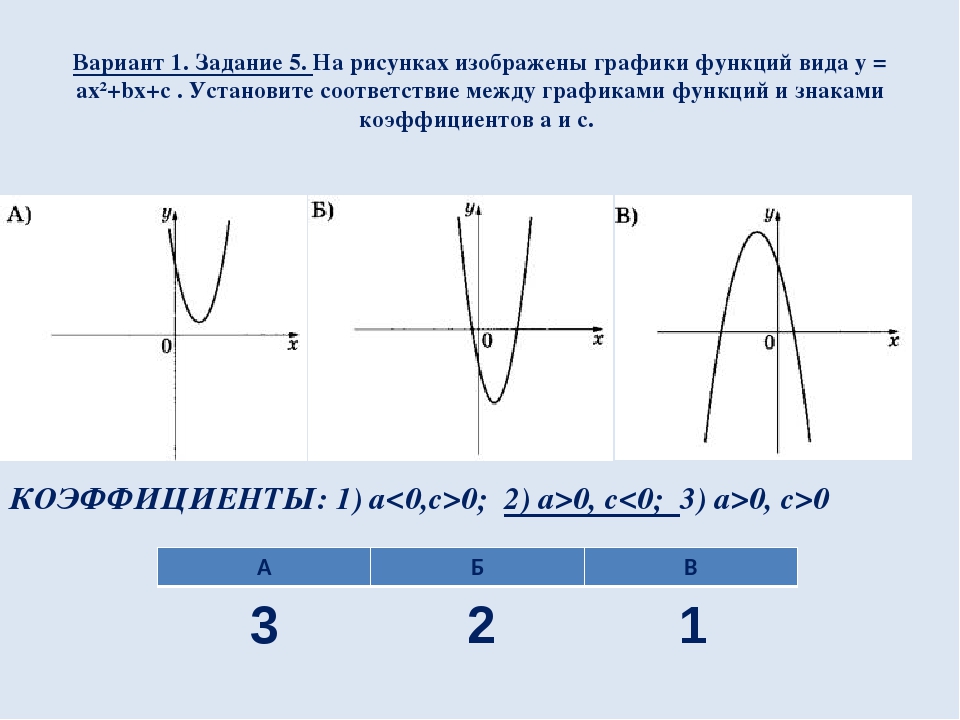
Вариант 1. Задание 5. На рисунках изображены графики функций вида y = ax²+bx+c . Установите соответствие между графиками функций и знаками коэффициентов a и c. КОЭФФИЦИЕНТЫ: 1) a<0,c>0; 2) a>0, c<0; 3) a>0, c>0 3 2 1 А Б В
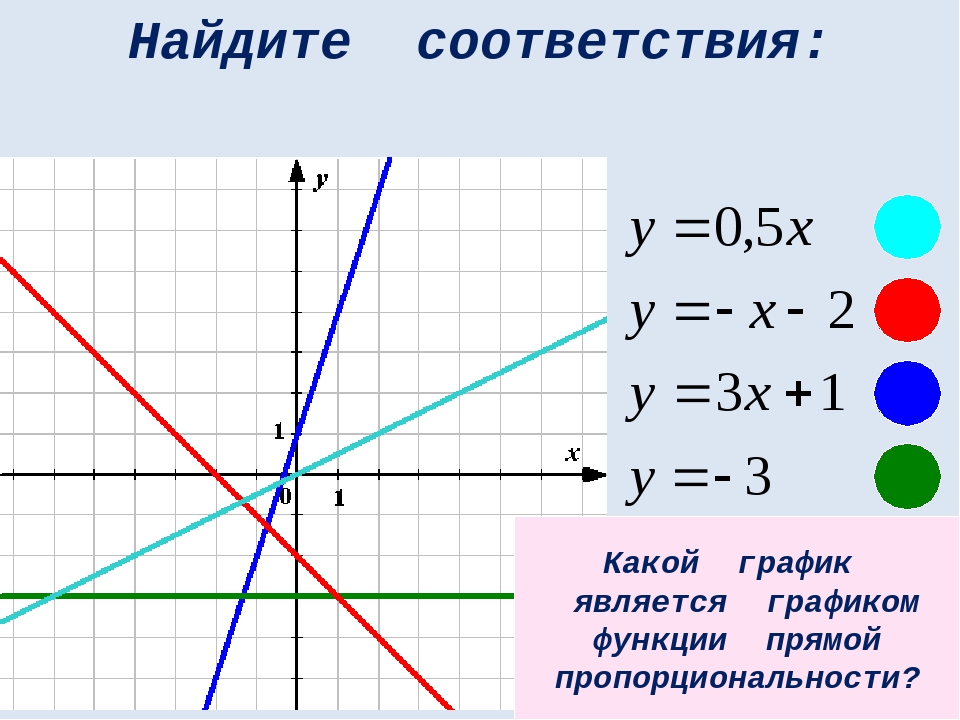
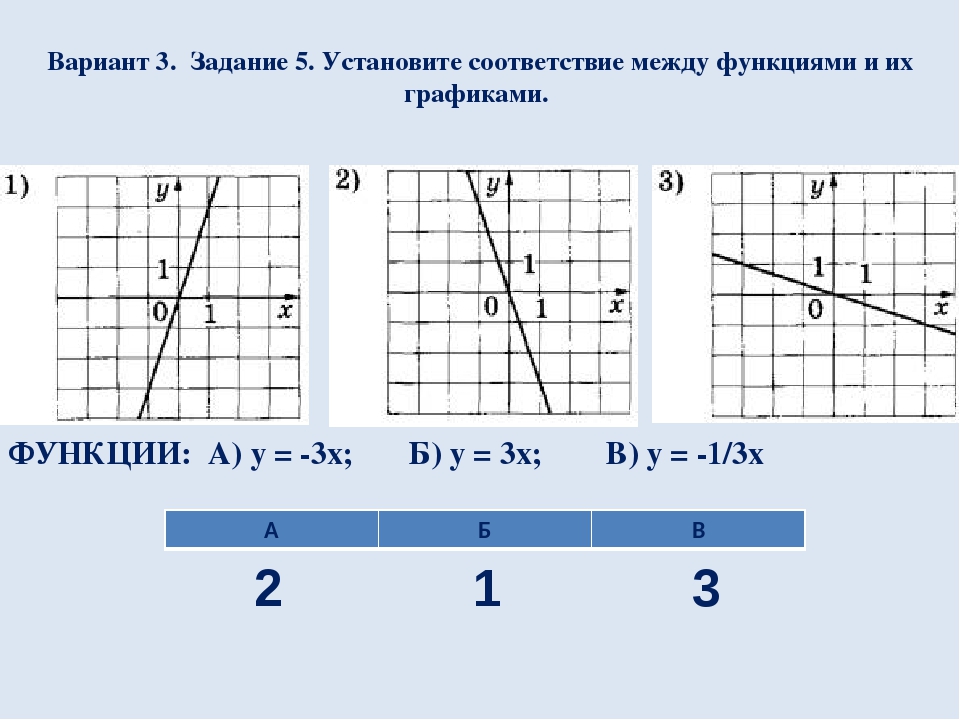
Вариант 3. Задание 5. Установите соответствие между функциями и их графиками. ФУНКЦИИ: А) y = -3x; Б) y = 3x; В) y = -1/3x 1 2 3 А Б В
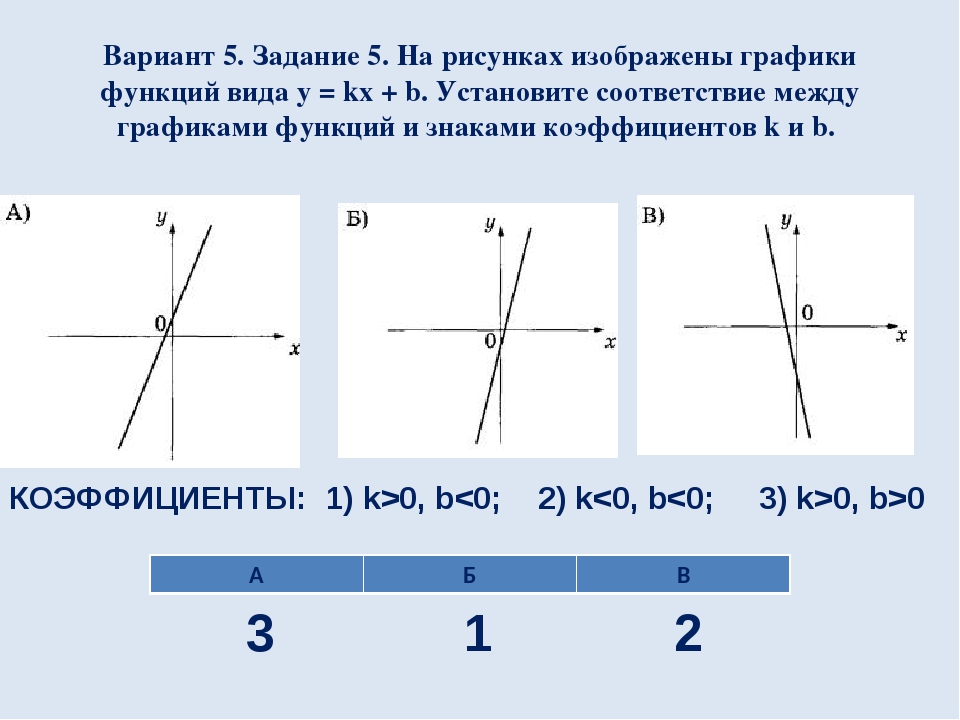
Вариант 5. Задание 5. На рисунках изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b. КОЭФФИЦИЕНТЫ: 1) k>0, b<0; 2) k<0, b<0; 3) k>0, b>0 2 3 1 А Б В
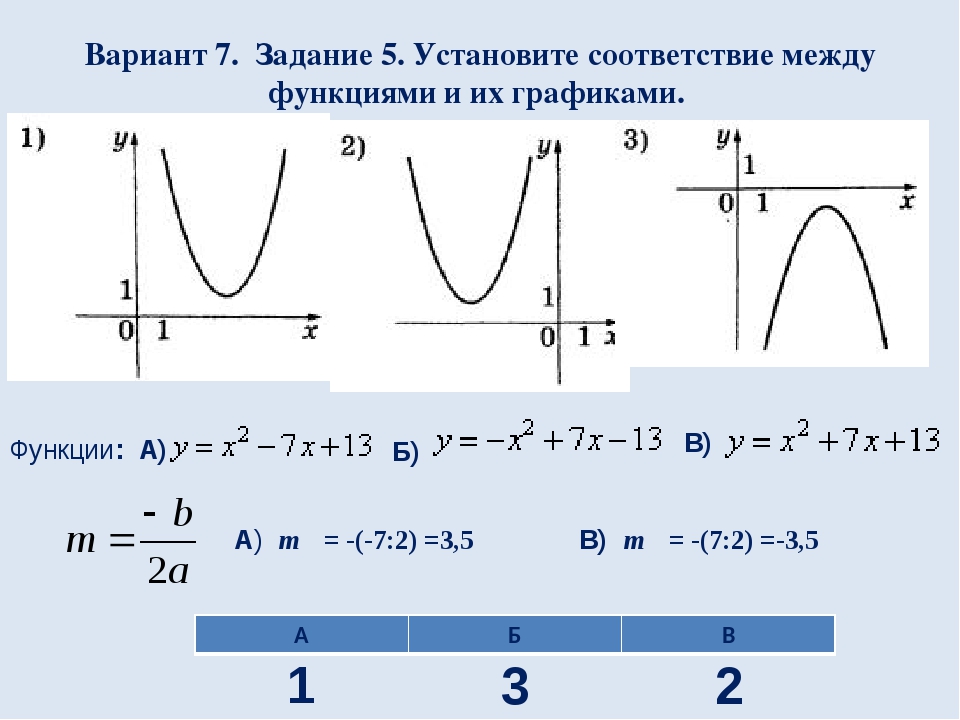
Вариант 7. Задание 5. Установите соответствие между функциями и их графиками. Функции: А) Б) В) 3 1 2 А) т = -(-7:2) =3,5 В) т = -(7:2) =-3,5 А Б В
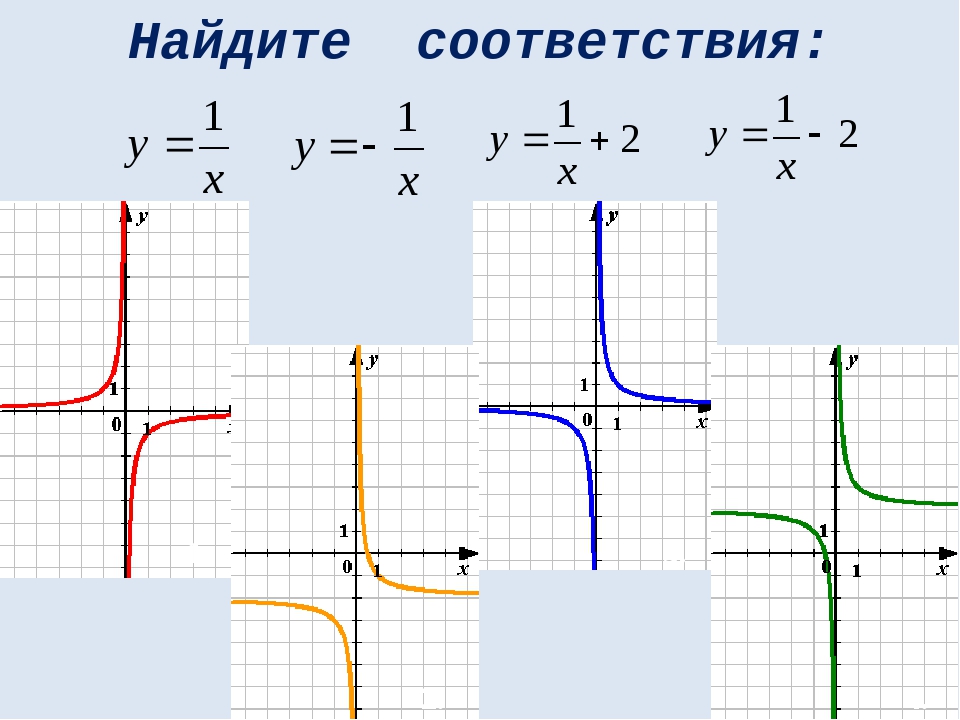
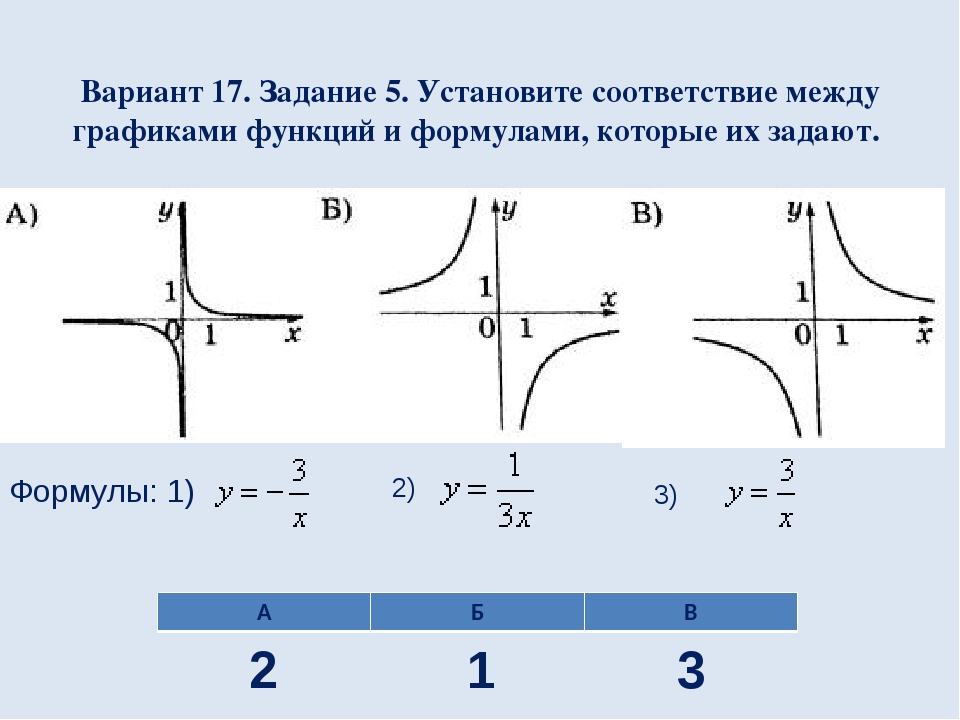
Вариант 17. Задание 5. Установите соответствие между графиками функций и формулами, которые их задают. Формулы: 1) 2) 3) 1 3 2 А Б В
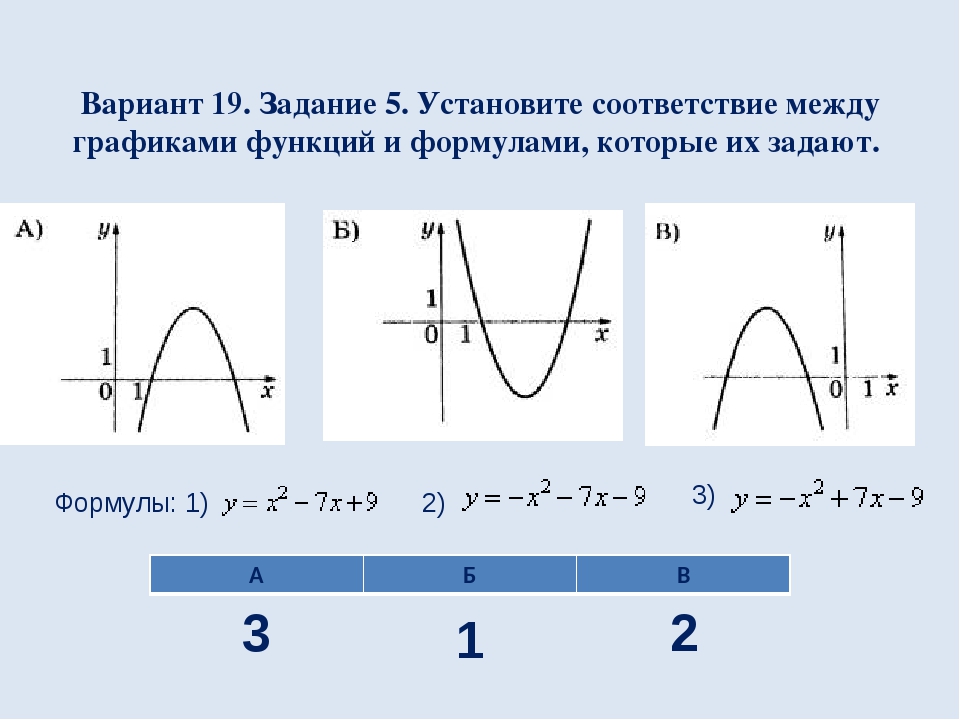
Вариант 19. Задание 5. Установите соответствие между графиками функций и формулами, которые их задают. Формулы: 1) 2) 3) 1 2 3 А Б В

| Автор | |
|---|---|
| Дата добавления | 20.05.2019 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4796 |
| Номер материала | 6223 |