
Презентация "Вписанная окружность"

Краткое описание документа:
Очень полезно использовать различные иллюстрации, демонстрировать их во время урока. Это упрощает работу учителя, ведь он не тратит лишнее время на записи на доске. Тем самым появляется дополнительное время для лучшего закрепления урока, для дополнительных практических заданий.
Презентация «Вписанная окружность» является отличным учебным пособием, которое поможет школьникам изучить вписанные окружности и их свойства. Тема является довольно объемной и информативной. В дальнейшем эти знания пригодятся при решениях различных задач.

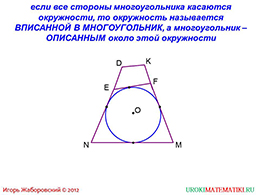
слайды 1-2 (Тема презентации "Вписанная окружность", определение вписанной окружности)
Для начала приводятся определения вписанной и описанной окружностей. Если окружность находится внутри какого-то многоугольника, то она является вписанной, при этом каждая сторона данного многоугольника должна касаться окружности. При этом фигуру, в которой находится окружность, называют описанной около этой окружности.
На примере можно увидеть, в каком случае окружность будет являться вписанной в многоугольник, в каком случае – не будет.
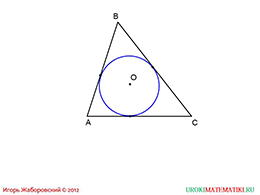
слайды 3-4 (примеры)
На следующем слайде приводится пример вписанной окружности в треугольник. Подробнее данная тема будет рассматриваться в дальнейшем. Мы видим, что каждая из трех сторон треугольника касается окружности, при этом имеет одну общую точку с ней.
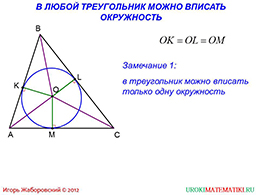
На следующем слайде говорится о том, что в абсолютно любой треугольник можно вписать окружность, причем, только одну. Доказывается это очень просто, используя предыдущие знания. Мы знаем, что радиусы любой окружности равны. Также, используя знания о касательной, можем определить, что все три стороны треугольника являются касательными для окружности.
слайд 5 (замечание)
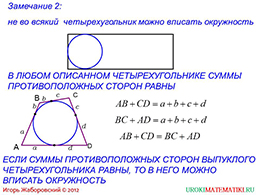
На следующем слайде рассматриваются вписанные окружности в четырехугольниках. Сразу же иллюстрируется пример прямоугольника, в который нельзя вписать окружность. Таким образом, напрашивается вывод, что не в любой четырехугольник можно вписать окружность.
Ниже рассматривается пример произвольного четырехугольника со вписанной окружностью. Каждая сторона является касательной и в точке пересечения, то есть точке касания, каждая сторона треугольника делится на две части. Исходя из этого, можно выразить суммы противоположных сторон четырехугольника. Можно увидеть, что суммы противоположных четырехугольников, в которых могут быть вписаны окружности, равны. Эта информация поможет при решении некоторых задач. Обратное высказывание будет тоже верно.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6116 |
| Номер материала | 354 |