
Урок "Теорема о пересечении высот треугольника"

Краткое описание документа:
Прежде чем приступать к рассмотрению данной теоремы стоит исследовать свойства срединных перпендикуляров, а также напомнить основные определения отрезков в любом классическом треугольнике. В данном видео уроке мы рассмотрим важнейшую теорему, затрагивающую особенности пересечения замечательных отрезков в плоском треугольнике.
Срединным перпендикуляром называют некий отрезок, который выходит из точки, лежащей на определенной стороне многоугольника, и делящей эту сторону на две равные части. При этом, угол между перпендикуляром и стороной, по определению равен 90 градусам. Согласно свойству треугольника на плоскости: точка пересечения всех трёх срединных перпендикуляров едина, и она равноудалена от всех вершин фигуры.
В геометрии существует понятие «замечательные точки», которое обозначает ряд важнейших точек в многоугольнике, являющихся определенным центром пересечения для некоторых характерных типов отрезков. К этим точкам относятся центры пересечения биссектрис, медиан, срединных перпендикуляров, высот многоугольника. В каждом случае фигуры, замечательные точки обладают своими личными свойствами и особенностями, которые позволяют, в том числе, характеризовать всю фигуру и решить множество смежных задач. Одной из важнейших замечательных точек является ортоцентр.
Согласно теореме о пересечении высот в треугольнике, все высоты плоского треугольника, или их продолжения за фигурой, пересекаются между собой в единой точке, именуемой ортоцентром данного треугольника. При этом, если треугольник является остроугольным, то ортоцентр его всегда будет лежать внутри фигуры. Если наличествует один тупой угол, то ортоцентр выносится за пределы треугольника.
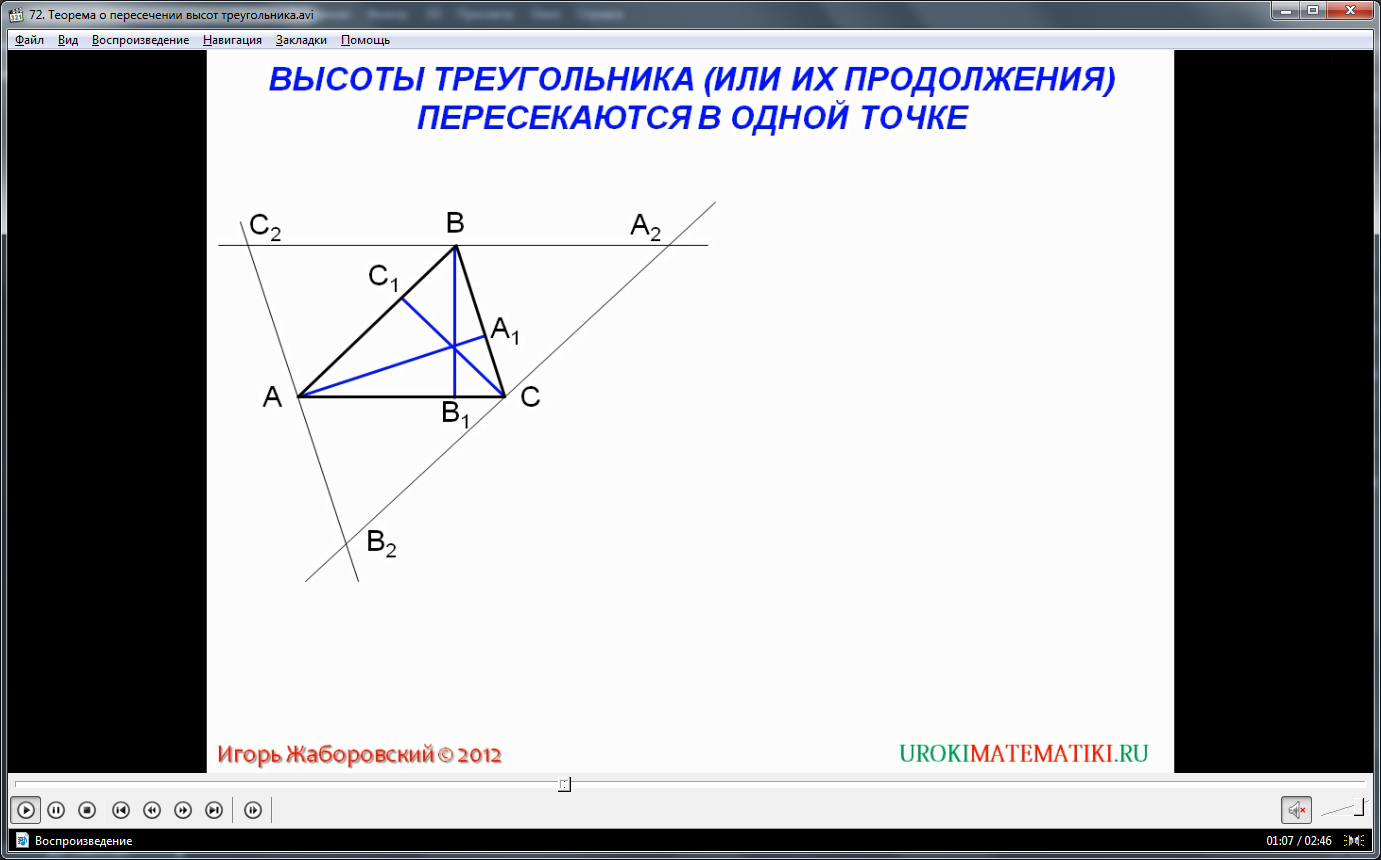
В представляемом видео тщательно рассмотрено доказательство этой важной теоремы. Для того, чтобы её утвердить, необходимо рассмотреть остроугольный треугольник с проведенными высотами, и дополнительно описанным внешним треугольником.
Построим треугольник АВС и проведем в нем три высоты – Н1 от стороны АС, Н2 от стороны ВС, Н3 от стороны ВА. Напомним, что высота – это отрезок, выходящий из угла треугольника, и пересекающий противолежащую сторону под углом 90 градусов. Т.е. угол ВН2А по определению равен 90, и т.д.
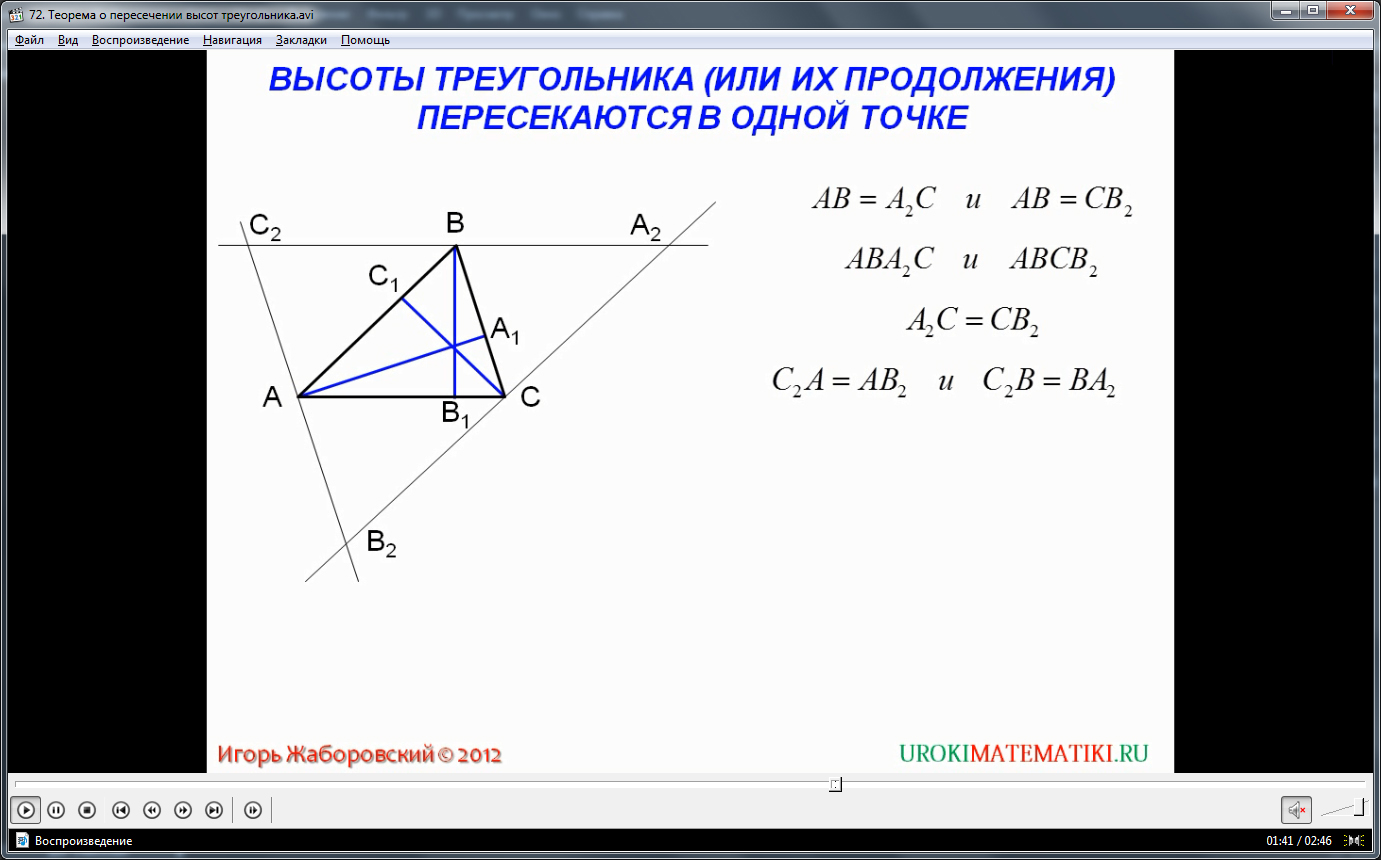
Построим описанный треугольник следующим образом: проведем от каждой вершине прямые, которые будут параллельными противолежащим сторонам. Отталкиваясь от точек пересечения трёх полученных прямых, определяем треугольник С2А2В2. По условию, С2В параллельно АС, при этом, С2ВСА – параллелограмм. По свойству этой фигуры С2В=АС, как противоположные стороны параллелограмма. Рассматривая параллелограмм ВАСА2, приходим к выводу, что АС = ВА2. Таким образом, С2В = АС = ВА2, отсюда следует, что С2В = ВА2, а точка В лежит строго посередине стороны С2А2.
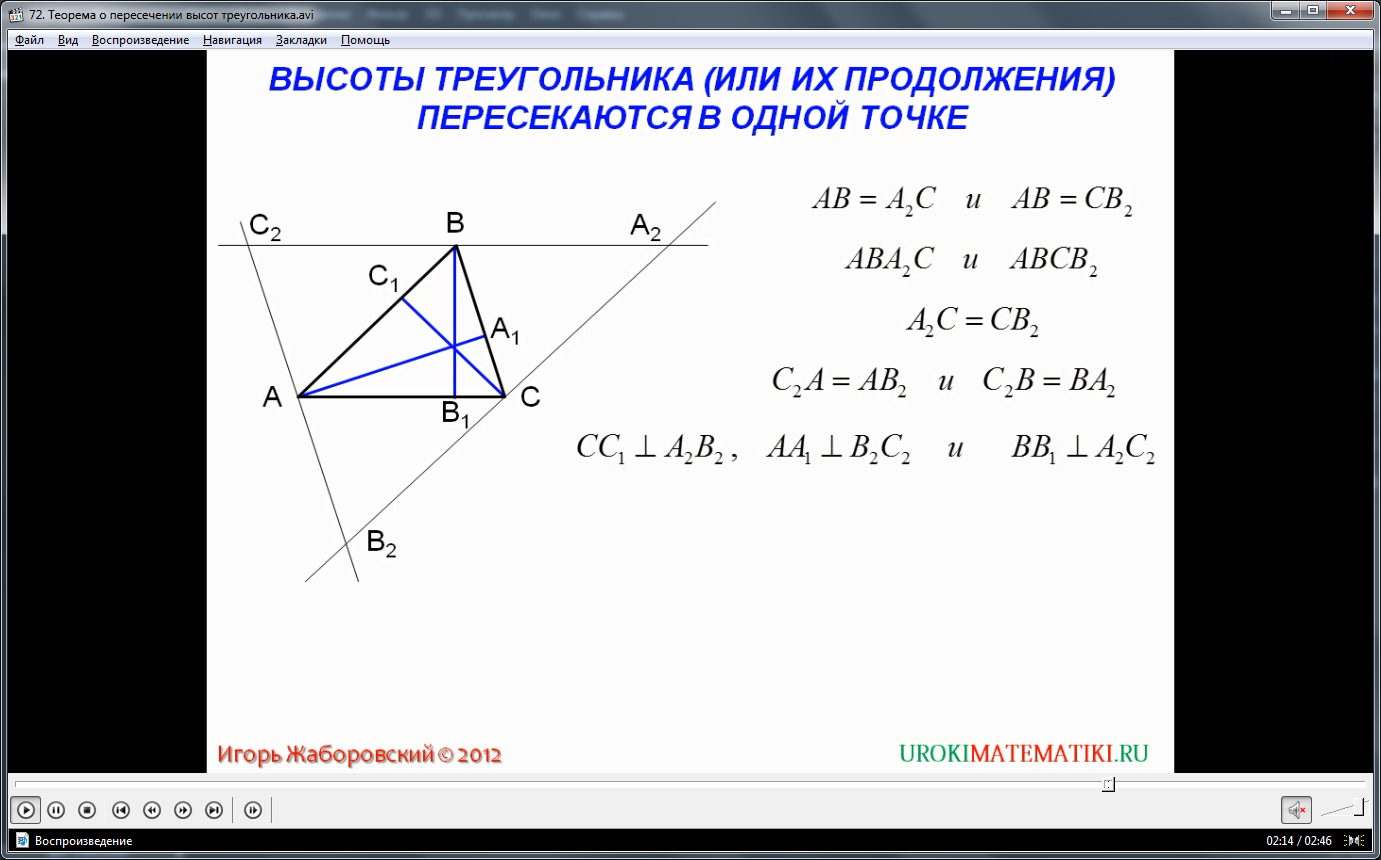
Кроме того, рассмотрим прямые С2А2, АС, являющиеся параллельными по условию, и секущую их ВН1. По аксиомам секущих, если угол ВН1С равен 90, а он равен этому значению по условию, ведь ВН1 высота, то А2ВН1 тоже равен 90, и отрезок ВН1 является, в итоге, срединным перпендикуляром для треугольника А2В2С2. Аналогичные рассуждения можно провести касательно каждой вершины треугольника АВС, в результате чего получим общий вывод – отрезки Н1, Н2, Н3 являются не только высотами треугольника АВС, но и срединными перпендикулярами треугольника А2В2С2. При этом мы прекрасно помним, что срединные перпендикуляры любого треугольника пересекаются в единой точке. Что и требовалось доказать.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5932 |
| Номер материала | 610 |