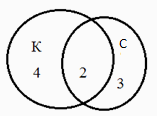Технологическая карта урока с презентацией на тему " Решение задач с помощью кругов Эйлера" 6 класс
Документы в архиве:
Название документа Мд-6 Круги Эйлера Ермаковой ЕИ.pptx












Описание презентации по отдельным слайдам:
Круги Эйлера Муниципальное казенное общеобразовательное учреждение «Ермаковская основная общеобразовательная школа» выполнила учитель математики Ермакова Е.И. д. Ермакова, 2020г.
Прозвенел уже звонок. Начинается урок. Посмотрите все ль в порядке: Книжки, ручки и тетрадки. Все друг к другу повернитесь Широко всем улыбнитесь, Улыбнитесь мне , гостям И садитесь по местам. Организационный момент
Проверочная работа Критерии отметки: 2 задания верно- «5» 1 задание верно-«3» 1 задание 2 задание 1 вариант 1.АUВ={2;3;5;7;8;9;12;15;17} А∩В={2;7;17} 9 2 вариант 1.АUВ={2;3;5;6;7;8;15;16;19} А∩В={3;8;19} 9
«Решение задач с помощью кругов Эйлера» Цель: рассмотреть способы решения задач с помощью кругов Эйлера; проводить логические рассуждения по сюжетам текстовых задач с помощью кругов Эйлера; отрабатывать умение использовать круги Эйлера для решения логических задач; где в повседневной жизни нам может пригодиться умение использовать Круги Эйлера; алгоритм решения задач с помощью кругов Эйлера.
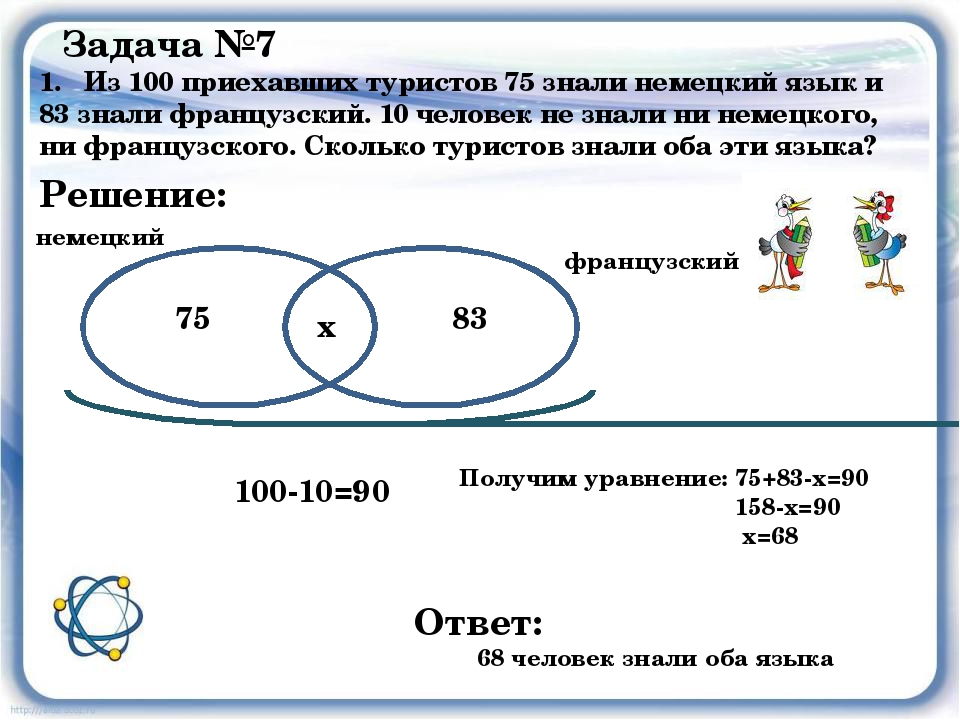
1. Из 100 приехавших туристов 75 знали немецкий язык и 83 знали французский. 10 человек не знали ни немецкого, ни французского. Сколько туристов знали оба эти языка? Задача №7 Решение: немецкий французский 75 83 х 100-10=90 Получим уравнение: 75+83-х=90 158-х=90 х=68 Ответ: 68 человек знали оба языка
Леонард Эйлер Леонард Эйлер, крупнейший математик XVIII века, родился в Швейцарии. В 1727г. по приглашению Петербургской академии наук он приехал в Россию. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира. Одним из первых, кто использовал для решения задач круги, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с кругами. Затем этот метод основательно развил швейцарский математик Леонард Эйлер. (1707 г.-1783 г.)
Фирма, поставляющая еду в школьную столовую, опросила 60 учеников о том, как они относятся к яблочному и виноградному сокам. Выяснилось, что 32 человека любят яблочный сок, 20 человек любят виноградный сок, а 14 человек любят и тот и другой сок. Сколько учеников из числа опрошенных не любит ни тот, ни другой сок? 18 14 1.32-14=18 учеников любят только яблочный сок 2.20-14=6 учеников только виноградный сок 6 3. 18+14+6=38 учеников любит хотя бы один из соков 4. 60- 38=22 ученика не любит ни один из соков
Алгоритм решения задач с помощью кругов Эйлера 1.Прочитать условие задачи. 2.Выполнить рисунок. 3.Записать данные в круги Эйлера. 4. Выполнить действия, анализируя и рассуждая, не забывая записывать результаты в части круга. 5.Записать ответ.
Меры длины – подняли руки, Меры площади- хлопнули в ладоши, Меры веса – зажмурились, Меры объема- присели. Физкультминутка
Возьмите за руку своего соседа по парте, улыбнитесь, посмотрите ему в глаза и скажите про себя: «Желаю тебе сегодня на уроке ….»
Название документа Техн.карта урока математики в 6 классе Круги Эйлера Ермаковой ЕИ.docx
Технологическая карта урока математики в 6 классе
УМК «Математика 6 класс» Г.В.Дорофеев
Тема урока: «Решение задач с помощью кругов Эйлера»
Тип урока: урок усвоения новых знаний
Цели урока:
образовательные: продолжать формирование умений выделять множества, подмножества, находить на изображениях область пересечения и объединения множеств; познакомить обучающихся с решением простейших логических задач методом кругов Эйлера; организовывать деятельность учащихся по изучению и выводу алгоритма решения задач с помощью кругов Эйлера.
развивающие: развивать умения видеть главное, существенное в изученном материале анализировать, сравнивать, обобщать, логически излагать свои мысли, делать выводы, развивать внимание; продолжать развитие логического и критического мышления, познавательного интереса к предмету.
воспитательные: воспитывать аккуратность и внимательность при решении логических задач; воспитывать ответственность через взаимопроверки, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, настойчивости для достижения цели; развивать самостоятельность, добросовестность .
Задачи урока:
Учебные задачи, направленные на достижение личностных результатов обучения:
Формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в творческом виде деятельности;
Развитие математических способностей;
Учебные задачи, направленные на достижение метапредметных результатов обучения:
Формирование умения видеть математическую задачу в контексте проблемной ситуации в окружающей жизни;
Формирование умения строить логические рассуждения и представлять информацию в понятной форме;
Учебные задачи, направленные на достижение предметных результатов обучения:
Формирование умений работать с математическим текстом, извлечение необходимой информации;
Овладение базовым понятийным аппаратом: развитие представления о множествах и операций с ними; овладение символьным языком математики;
Формирование умений точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику.
Планируемые результаты:
Личностные: грамотно излагать свои мысли, анализировать, сравнивать. Развивать познавательный интерес через творческие задания. Планировать собственную деятельность, определять средства для ее осуществления. Уметь самостоятельно контролировать свое время и управлять им. Развивать активность и находчивость при решении задач, умение общаться в коллективе.
Предметные: проводить логические рассуждения по сюжетам текстовых задач с помощью кругов Эйлера, отрабатывать умение использовать круги Эйлера для решения логических задач.
Метапредметные: проводить анализ высказываний, выделять аналогию при решении задач, осуществлять поиск и выделение необходимой информации, выбирать более удобный способ решения. Понять роль и значение Кругов Эйлера для решения задач в окружающей жизни.
Технология: технология обучения в сотрудничестве, ИКТ-технологии, здоровьесберегающие технологии
Методы обучения:
Словесный
Наглядный
Исследовательский
Частично-поисковый
Репродуктивный
Формы организации познавательной деятельности учащихся: фронтальная, работа в парах, индивидуальная, групповая.
Основные понятия, изучаемые на уроке: круги Эйлера, операции над множествами, такие как, пересечение и объединение множеств
Оборудование: компьютер, проектор, фломастеры, карандаши, листы А4, шаблоны кругов (разного диаметра), карточки с задачами
План урока:
Организационный этап 1 мин
Мотивация и актуализация знаний 7 мин
Первичное усвоение новых знаний 10 мин
Первичная проверка понимания (истор.справка ) 7 мин +1 мин
Физкультминутка 3 мин
Первичное закрепление 7 мин
Рефлексивно-оценочный этап 2 мин
Информация и инструктаж о домашнем задании 2 мин
Технологическая карта урока
| Этап урока, время этапа | Задачи этапа | Формы учебного взаимодействия | Деятельность учителя | Деятельность учащихся | Формируемые УУД и предметные действия |
| Организационный этап, 1 мин | создать благоприятный психологический настрой на работу | Фронталь-ная | Приветствует обучающихся, организует начало урока . и готовность к восприятию материала. Слайд 2 Прозвенел уже звонок. Начинается урок. Посмотрите все ль в порядке: Книжки, ручки и тетрадки. Все друг к другу повернитесь Широко всем улыбнитесь, Улыбнитесь мне , гостям И садитесь по местам. | -Включаются в ритм урока -Приветствуют учителя, -настраиваются на успешное изучение материала урока -проверяют готовность к уроку | Личностные: самоопределение. Коммуникативные: настрой на изучение предмета, планирование учебного сотрудничества с учителем и сверстниками. |
| Мотивация и актуализация знаний, 3+4 мин | -Отрабатывать навыки устных вычислений -Вызвать эмоциональный настрой и познавательный интерес к теме; - организовать самостоятельное формулирование вопросов и постановку цели | фронталь-ная, групповая | 1.Откройте тетради с домашним заданием :проверяют (написано на доске в перемену) 2.Запишите в тетради сегодняшнюю дату. Выполним проверочную работу. (можно в группах, можно фронтально 1 вариант)(см. Приложение 1): Вариант 1 1.Даны множества: А={2;5;7;8;12;17} и В={2;3;7;9;15;17}. Найдите объединение и пересечение этих множеств. 2. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро - собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг? Вариант 2 1.Даны множества: А={3;5;6;8;15;19} и В={2;3;7;8;16 ;19}. Найдите объединение и пересечение этих множеств. 2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро – фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг? Проверяем задание №1 и №2работы на слайде 3(на слайде только ответы) Поднимите, пожалуйста, руку у кого за сам.раб. отметка «5», а теперь те у кого- «4». А чью работу оценили отметкой «3». Ребята у вас есть возможность исправить свои отметки по ходу урока. Хорошо? - Откройте тетради, которые вам выдали ,запишите число, оставьте место для темы . Подготовка к восприятию нового способа действия. Спрашиваю: кто и каким способом решил задачу, предлагаю способ кругов Эйлера(не называя) Решение: Можно, конечно, «угадать» в процессе замысловатых рассуждений, можно – посредством вот таких действий:
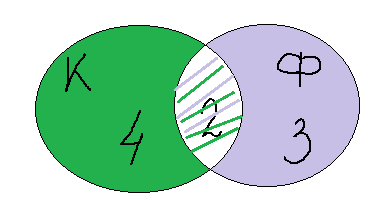
Но как грамотно обосновать их? Как ответить на вопрос, что получилось в результате первого действия? Леонард Эйлер придумал очень красивый способ решения таких задач, который назвали кругами Эйлера. Вот он. Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом – фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 (т.к. кактусы и фиалки у двоих). В оставшейся части «кактусового» круга ставим цифру 4 (всего кактусы – у шестерых, а у двух мы уже учли). В свободной части «фиалкового» круга ставим цифру 3 (5 – 2 = 3). А теперь сам рисунок подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.
Задаю вопросы. Так как можно сформулировать тему нашего урока? - Итак, мы сегодня будем говорить о кругах Эйлера. А какие цели на урок мы можем поставить ? слайд № 4 Для чего мы их будем использовать? Молодцы! Запишите тему урока: «Решение задач с помощью кругов Эйлера»
По ходу урока мы узнаем утверждение Эйлера, которое актуально по сей день.(дать при наличии времени в конце урока для рефлексии)- эпиграф(см. этап рефлексии) | -Открывают тетради, проверяют домашнее задание (проверяют каждый свою работу) -записывают дату, Работают в парах, выполняют задание. АUВ= {2;3;5;7;8;9;12;15;17} А∩В={2;7;17} АUВ= {2;3;5;6;7;8;15;16;19} А∩В={3;8;19} Тетрадями поменялись, проверяем красной пастой Проверили Критерии: 2 зад. верно- «5» 1 зад. верно-«3» поставили оценки, тетрадь закрыли, положили на край стола, сдадут в конце урока, чтобы учитель проверил еще раз. -решают проверочную работу в парах оставляют место для темы Работают с учителем в тетрадях (круги чертят по шаблонам) Формулируют и записывают тему урока Формулируют цели урока Отвечают на вопросы | Личностные УУД: проявлять интерес к новому содержанию Познавательные УУД: Вычислять примеры устно Регулятивные УУД: определять цели учебной деятельности Коммуникативные УУД Взаимодействуют с учителем во время опроса, осущест вляемого во фрон тальном режиме, слушают одноклассника, высказывает возражения. |
| Этап первичного усвоения новых знаний 10 мин Первичная проверка понимания 7 мин | • организовать осмысленное восприятие новой информации | Фронталь-ная. Индивидуальная. Самостоятельная. | Давайте попробуем применить круги Эйлера для решения задачи из варианта 1 (сильный ученик пробует у доски по аналогии) Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом - собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части "кошачьего" круга ставим цифру 4 (6 - 2 = 4). В свободной части "собачьего" круга ставим цифру 3 (5 - 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг. Ответ. 9 подруг. Молодец! Рассмотрим решение еще одной задачи на слайде №5 1. Из 100 приехавших туристов 75 знали немецкий язык и 83 знали французский. 10 человек не знали ни немецкого, ни французского. Сколько туристов знали оба эти языка? Послушаем историческую справку.(слайд № 6) Историческая справка В математике рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Вы знаете, что соотношения между множествами принято иллюстрировать с помощью кругов. Обычно их называют кругами Эйлера- по имени великого ученого Леонарда Эйлера(1707-1783).Математик, механик, физик, астроном, Л.Эйлер родился и вырос в Швейцарии, а работал в основном в России и Германии. За свою жизнь Л.Эйлер написал более 850 научных работ. В одной из них и появились круги, которые, по его словам, «очень подходят для того, чтобы облегчить наши рассуждения». В 1727 г. по приглашению Петербургской академии наук он приехал в Россию, где работал долгие годы. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал первым математиком мира. 2) Решим с помощью кругов Эйлера задачу на слайде № 7 Фирма, поставляющая еду в школьную столовую, опросила 60 учеников о том, как они относятся к яблочному и виноградному сокам. Выяснилось, что 32 человека любят яблочный сок, 20 человек любят виноградный сок, а 14 человек любят и тот и другой сок. Сколько учеников из числа опрошенных не любит ни тот, ни другой сок? -В условии этой задачи не так легко разобраться. Ведь если сложить 32, 20 и 14, то получится больше, чем 60. Поэтому, чтобы найти ответ обратимся к кругам Эйлера. Делаем схему и решаем задачу.
-Итак, перечислим наши действия: Записали, сколько любят и тот и другой сок, потом, вычислили, сколько любят только яблочный или виноградный сок, затем, узнали, сколько любят хотя бы один из соков и вычислили, сколько не любят ни один из соков. Каким же получается алгоритм решения задач с помощью кругов Эйлера? Слайд № 8 1.Прочитать условие задачи. 2.Выполнить рисунок. 3.Записать данные в круги Эйлера. 4. Выполнить действия, анализируя и рассуждая, не забывая записывать результаты в части круга. 5.Записать ответ. Раздаёт карточки с алгоритмом Вы задач много решали и ,наверно, все устали. Давайте немного отдохнем и снова решать начнем. | Рисуют круги в тетради. Вписывают данные Работают индивидуально Подготовленные до урока ученики рассказывают (с места, дать всем домой) Остальные слушают сообщение. Контроль-комбинированная форма Перечисляют шаги под руководством учителя. | Личностные УУД: Проявлять желание применить на практике свои знания. Познавательные УУД: извлекать необходимую информацию из прослушанных текстов; структурировать знания; Коммуникативные УУД: вступать в диалог, с достаточной полнотой и точностью выражать свои мысли, доказывать, аргументировать свою точку зрения. Регулятивные УУД: Контролировать правильность и точность ответов одноклассников. - |
| Физминутка 3 мин | Снятие эмоционального напряжения. | Фронталь-ная | 1.Показ физминутки на слайде № 9 Учитель называет единицу измерения – ученик выполняет действие. .(текст см. ниже) Меры длины – подняли руки, Площади- хлопнули в ладоши, Веса – зажмурились, Объема- присели
| Выполняют упражнения | |
| Первичное закрепление. 7 мин | Обеспечить осмысленное усвоение и закрепление знаний. Проверить усвоение данной темы | Групповая | Давайте закрепим красивый способ решения задач Леонарда Эйлера. -Напишите : самостоятельная работа по вариантам. Организует самостоятельную работу учеников, управление их учебными действиями; развивает навыки исследовательской деятельности Найдите задачу на карточке. Решите её с помощью кругов Эйлера. Отразите круги на листе бумаги так, чтобы всем потом было видно. Перед решением давайте ещё раз назовём алгоритм решения задач с помощью кругов Эйлера.Вар. 2 Работа по учебнику с 219.№ 835 Вар.1 В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – в музее. Планетарий и цирк посетили 5 учеников; планетарий и музей – 3, цирк и музей– 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места? .(cм. Приложение) Всё ли получилось? Давайте выслушаем представителей групп, какой получился ответ задачи. Затем, каждая группа проверяет решение по эталону.(мой листок)(cм. Приложение) | Называют алгоритм Делятся на группы : Один читает вслух, остальные слушают. 1 гр- Б.В., Ф.Н,- вар.2 2 гр- Е.Ж,,К.Н..(задача сложнее)- вар. 1 Поочерёдно предъявляют свои ответы Делают иллюстрации Решение 19-5-3=11(ч)- п 6-3-1=2(ч)- с 10-5-1=4(ч) –ц 11+2+4+5+3+1+3=29 (ч)-в классе Контроль – групповая форма | |
| Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения, учатся сотрудничать с учителем и одноклассниками. Личностные: учатся замечать и признавать свои ошибки, прислушиваться к мнениям и взглядам одноклассников, анализировать Коммуникативные: приобретают умения организовать сотрудничество с партнёром, адекватно использовать речевые средства для решения коммуникативных задач, осуществлять контроль, коррекцию, оценку действий партнера. Познавательные: устанавливают причинно-следственные связи между объектами, правильный ход действий. Выявляются границы применимости нового знания. | |||||
| Рефлексивно-оценочный этап, 2 мин Информация и инструктаж о домашнем задании 2 мин | осмысление процесса и результата деятельности оценить содержание этапов урока | Индиви-дуальная, фронталь-ная | Понравилось вам использовать метод кругов Эйлера для решения задач? Давайте обсудим слова Эйлера. (вывесить фразу). «… круги очень подходят для того, чтобы облегчить наши размышления» Леонард Эйлер Согласны ли вы, что «круги облегчают наши размышления»? Достигнута ли наша цель урока? Вы молодцы и заслужили пятёрки. Ребята, уходя с урока, опустите смайлик в ту ячейку, которая оценивает вашу деятельности на уроке.слайд №11 Задает домашнее задание: Учебник №839, рис 10.10. или придумать задачу, решаемую с помощью кругов Эйлера. Дополнительное задание (для тех, кто желает исправить плохие или получить отметки) | Обсуждают фразу Эйлера Опускают смайлик в ту ячейку, которая оценивает деятельности на уроке. Записывают дом. задание. | Регулятивные УУД: констатировать необходимость продолжения действий Коммуникативные УУД: адекватно отображать свои чувства, мысли в речевом высказывании |
Круги Эйлера — наглядная геометрическая иллюстрация понятий и отношений между элементами множествами. Применительно к логическим операциям: это пересечения, и объединения множеств, представленные в виде кругов Эйлера.
Многие из нас даже не задумываются над тем, что множество имеет большое значение в нашей жизни. Любая область человеческой деятельности связана не только с одним предметом, объектом, а с целой совокупностью.
Например: медицина изучает не одну отдельно взятую болезнь, а все болезни; зоология изучает не отдельно взятое животное, а совокупность всех животных, анализ успеваемости,
мир увлечений, участие во внеклассных занятиях. Математика, как и другая область человеческих знаний, изучает те или иные объекты не каждый в отдельности, а в их связи между собой.
Приложения
Проверочная работа (напечатано на листе А4 для каждого ученика)
Вариант 1
1.Даны множества: А={2;5;7;8;12;17} и В={2;3;7;9;15;17}. Найдите объединение и пересечение этих множеств.
2. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро - собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг?
Вариант 2
1.Даны множества: А={3;5;6;8;15;19} и В={2;3;7;8;16 ;19}. Найдите объединение и пересечение этих множеств.
2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро – фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
Самостоятельная работа
Вариант 2. Работа по учебнику с 219.№ 835
Вариант 1 В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – в музее. Планетарий и цирк посетили 5 учеников; планетарий и музей – 3, цирк и музей– 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?
Дополнительные задачи на урок (напечатано на листе А4 для каждого ученика)
1. На спортивные соревнования в ЛМШ ходили 220 школьников. При этом некоторые из них участвовали в чемпионатах, а остальные были зрителями. В легкоатлетической эстафете приняли участие 30 человек, в соревнованиях по волейболу – 26, пионерболу – 32, футболу – 31, шахматам – 28 и теннису – 36 человек. 53 школьника приняли участие более чем в одном соревновании; из них 24 школьника участвовали 3 или более раз, 9 школьников – не менее 4 раз и 3 школьника – даже 5 раз (в последнюю тройку входит и один чудак, который выступал во всех шести соревнованиях). Сколько из школьников были зрителями?
2. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским – 10, немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком?
Физкультминутка
| Меры длины | мм | версту | аршин | вершок | сажень |
| Меры площади | км2 | сотка | м2 | десятина | копна |
| Меры веса | кг | Безмен | пуд | т | золотник |
| Меры объема | 1 л | 1 дм3 | Ушат | 1 см3 | Крынка |
Дополнительные задачи на урок(напечатано на листе А4 для каждого ученика)
5) на круги Эйлера
1. На спортивные соревнования в ЛМШ ходили 220 школьников. При этом некоторые из них участвовали в чемпионатах, а остальные были зрителями. В легкоатлетической эстафете приняли участие 30 человек, в соревнованиях по волейболу – 26, пионерболу – 32, футболу – 31, шахматам – 28 и теннису – 36 человек. 53 школьника приняли участие более чем в одном соревновании; из них 24 школьника участвовали 3 или более раз, 9 школьников – не менее 4 раз и 3 школьника – даже 5 раз (в последнюю тройку входит и один чудак, который выступал во всех шести соревнованиях). Сколько из школьников были зрителями?
Решение: В сумме в них были 30 + 26 + 32 + 31 + 28 + 36 = 183 школьника. Число школьников, игравших хотя бы один раз, равно 183 – 53 – 24 – 9 – 3 – 1 = 93. Оставшиеся 127 школьников были зрителями.
2. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским – 10, немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком?
Решение: только английским владеет 13 человек, только французским – 30, только немецким – 20 человек. 20 человек не знают ни одного из этих языков.
Дополнительное задание на дом
(для тех, кто желает исправить плохие или получить отметки)
Леонард Эйлер принадлежит к числу гениальных математиков всех времен. Он родился в Швейцарии в небольшом городке.
1) Чтобы узнать город, отметь точки на числовом луче. Единичный отрезок – 3 клетки Ь(4); Е(); Б(); З(2); Л(3) ; А(). Удивительно, но, будучи еще ребенком, он начинает посещать лекции великого математика Иоганна Бернулли.
Спустя х лет он по приглашению Петербургской академии наук выехал в Россию.
2) Определи х:
7 8 56
16 3 48
20 х 80
С этого времени началось быстрое развитие его научной деятельности. Из номера в номер журнал Академии печатал его математические работы.
3) Как назывался журнал, узнаешь, «прополов сорняки». Выбери из данного текста три названия сорных растений, тогда оставшиеся буквы и составят название журнала:
КОСОТОЛЕМБЕДАМЕКРАНПИТАВАРИИ
4) Ученый написал свыше 800 работ, из них по математике. Сколько математических трудов создано ученым?
В одной из своих работ Эйлер, чтобы «облегчить наши размышления», предложил использовать круги.
5) Перед учащимися лежит карточка с закодированным в ней словом. Расположите дроби в порядке убывания и узнайте слово.
| Й | Р | Э | Е | Л |
Решите задачи:
1-в: 12 моих одноклассников любят читать детективы, 18-фантастику, трое из них с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
2-в: Из 80 туристов, приехавших в Москву, 52 хотят посетить Большой театр, 30- Малый театр, 12 хотят посетить оба театра, остальные в театры ходить не хотят. Сколько человек не собираются идти в театр?
В математике рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер.
Вы знаете, что соотношения между множествами принято иллюстрировать с помощью кругов. Обычно их называют кругами Эйлера- по имени великого ученого Леонарда Эйлера(1707-1783).Математик, механик, физик, астроном, Л.Эйлер родился и вырос в Швейцарии, а работал в основном в России и Германии. За свою жизнь Л.Эйлер написал более 850 научных работ. В одной из них и появились круги, которые, по его словам, «очень подходят для того, чтобы облегчить наши рассуждения».
В 1727 г. по приглашению Петербургской академии наук он приехал в Россию, где работал долгие годы. Эйлер попал в круг выдающихся математиков, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал первым математиком мира.
Проверочная работа (напечатано на листе А4 для каждого ученика)
Вариант 1
1.Даны множества: А={2;5;7;8;12;17} и В={2;3;7;9;15;17}. Найдите объединение и пересечение этих множеств.
2. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро - собак. И только у двоих есть и те и другие. Угадайте, сколько у меня подруг?
Вариант 2
1.Даны множества: А={3;5;6;8;15;19} и В={2;3;7;8;16 ;19}. Найдите объединение и пересечение этих множеств.
2. Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро – фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?
Самостоятельная работа
Вариант 2. Работа по учебнику с 219.№ 835
Вариант 1 В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – в музее. Планетарий и цирк посетили 5 учеников; планетарий и музей – 3, цирк и музей– 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?
Дополнительные задачи на урок (напечатано на листе А4 для каждого ученика)
1. На спортивные соревнования в ЛМШ ходили 220 школьников. При этом некоторые из них участвовали в чемпионатах, а остальные были зрителями. В легкоатлетической эстафете приняли участие 30 человек, в соревнованиях по волейболу – 26, пионерболу – 32, футболу – 31, шахматам – 28 и теннису – 36 человек. 53 школьника приняли участие более чем в одном соревновании; из них 24 школьника участвовали 3 или более раз, 9 школьников – не менее 4 раз и 3 школьника – даже 5 раз (в последнюю тройку входит и один чудак, который выступал во всех шести соревнованиях). Сколько из школьников были зрителями?
2. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским – 10, немецким и французским – 5, всеми тремя языками – 3. Сколько туристов не владеют ни одним языком?
Лист для проверки самостоятельной работы по образцу
Вариант 2. Работа по учебнику с 219.№ 835
Вариант 1 В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – в музее. Планетарий и цирк посетили 5 учеников; планетарий и музей – 3, цирк и музей– 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?
САМОАНАЛИЗ УРОКА ПО ФГОС
Вариант №1
Данный урок (по предмету .математика) является уроком №5… в системе уроков по разделу Множества. Комбинаторика Тема урока: (назвать тему Решение задач с поощью кругов Эйлера …)
Цели урока: образовательные…, воспитательные…, развивающие….
образовательные: продолжать формирование умений выделять множества, подмножества, находить на изображениях область пересечения и объединения множеств; познакомить обучающихся с решением простейших логических задач методом кругов Эйлера; организовывать деятельность учащихся по изучению и выводу алгоритма решения задач с помощью кругов Эйлера.
развивающие: развивать умения видеть главное, существенное в изученном материале анализировать, сравнивать, обобщать, логически излагать свои мысли, делать выводы, развивать внимание; продолжать развитие логического и критического мышления, познавательного интереса к предмету.
воспитательные: воспитывать аккуратность и внимательность при решении логических задач; воспитывать ответственность через взаимопроверки, способствовать пониманию необходимости интеллектуальных усилий для успешного обучения, настойчивости для достижения цели; развивать самостоятельность, добросовестность .
В данном классе я поставила следующие задачи (указать задачи), направленные на формирование УУД (личностные:…, познавательные: …, коммуникативные: …, регулятивные: …)
Задачи урока:
Учебные задачи, направленные на достижение личностных результатов обучения:
Формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в творческом виде деятельности;
Развитие математических способностей;
Учебные задачи, направленные на достижение метапредметных результатов обучения:
Формирование умения видеть математическую задачу в контексте проблемной ситуации в окружающей жизни;
Формирование умения строить логические рассуждения и представлять информацию в понятной форме;
Учебные задачи, направленные на достижение предметных результатов обучения:
Формирование умений работать с математическим текстом, извлечение необходимой информации;
Овладение базовым понятийным аппаратом: развитие представления о множествах и операций с ними; овладение символьным языком математики;
Формирование умений точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику.
В результате проведенного урока я предполагала получить следующие результаты:. .
Планируемые результаты:
Личностные: грамотно излагать свои мысли, анализировать, сравнивать. Развивать познавательный интерес через творческие задания. Планировать собственную деятельность, определять средства для ее осуществления. Уметь самостоятельно контролировать свое время и управлять им. Развивать активность и находчивость при решении задач, умение общаться в коллективе.
Предметные: проводить логические рассуждения по сюжетам текстовых задач с помощью кругов Эйлера, отрабатывать умение использовать круги Эйлера для решения логических задач.
Метапредметные: проводить анализ высказываний, выделять аналогию при решении задач, осуществлять поиск и выделение необходимой информации, выбирать более удобный способ решения. Понять роль и значение Кругов Эйлера для решения задач в окружающей жизни.
Это урок (указать тип урока). урок усвоения новых знаний
Он включал в себя (указать количество) 8 этапов (структура урока).
План урока:
Организационный этап 1 мин
Мотивация и актуализация знаний 7 мин
Первичное усвоение новых знаний 10 мин
Первичная проверка понимания (истор.справка ) 7 мин +1 мин
Физкультминутка 3 мин
Первичное закрепление 7 мин
Рефлексивно-оценочный этап 2 мин
Информация и инструктаж о домашнем задании 2 мин
При проведении урока я использовала современные образовательные технологии в соответствии с требованиями ФГОС (назвать 1 или несколько технологий) технология обучения в сотрудничестве, ИКТ-технологии, здоровьесберегающие технологии
и использовала их на следующих этапах урока (указать этапы урока).
Чтобы добиться цели урока, я подобрала … (содержание урока: примеры, вопросы, задания), соответствующие возрастным особенностям.
Материал урока оказался … (сложным, легким, интересным для учащихся и др.).
В ходе урока была организована … (индивидуальная, фронтальная, групповая, коллективная) работа учащихся.
Наиболее эффективной оказался (указать вид работы), потому что (указать причину).
Соотношение деятельности учитель-ученик соответствует/ не соответствует реализации личностно ориентированного подхода в обучении: (применение диалоговых форм общения, создание проблемных ситуаций, осуществление обратной связи, объем и характер самостоятельной работы).
На уроке мною использовались следующие средства обучения: (наглядный материал, различные источники информации и др.).
Темп урока быстрый/медленный; монотонный/динамичный/; исходя из возможностей класса.
Распределение времени было рациональное/нерациональное.
Мне удалось/не удалось уложиться по времени.
Мне было (легко/тяжело) вести урок. Учащиеся включались в работу (активно, неохотно, тяжело).
Меня порадовали … , удивили … , огорчили … (кто из учащихся?), потому что ….
Результаты урока совпадают/не совпадают с целью урока.
Я полагаю, что все научились …, что подтверждают результаты самоконтроля и самооценки учащихся.
Домашнее задание имеет (оптимальный объем, предоставление права выбора, доступность и др.), поэтому (не) вызовет затруднения у учащихся.
В целом урок можно считать ….состоявшимся.
Название документа Из истории кругов Эйлера в уголок.docx
Из истории кругов Эйлера
Часто множество изображают кругами, эти круги обычно называют «кругами Эйлера» по имени величайшего математика Леонарда Эйлера.
Леонард Эйлер (Euler) (1707 – 1783 г.г.) – математик, механик, физик и астроном. По происхождению швейцарец, а работал в основном в Росси и в Германии. В 1726 году был приглашен в Петербургскую Академию наук и в 1727 году переехал в Россию. В 1741 – 1766 годах работал в Берлине, член Берлинской Академии наук. Эйлер – ученый необычайной широты интересов и творческой продуктивности. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки.
Одним из первых, кто разрабатывал метод решения задач с помощью кругов Эйлера, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 – 1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил швейцарский математик Леонард Эйлер (1707 – 1783). Он долгие годы работал в Петербургской Академии наук. К этому времени относятся его знаменитые «Письма к немецкой принцессе», написанные в период с 1761 по 1768 год. В некоторых из этих «Писем…» Эйлер как раз и рассказывает о кругах, которые «очень подходят для того, чтобы облегчить наши размышления». После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848).
Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов пользовался и немецкий математик Эрнест Шредер (1841 – 1902). Этот метод широко используется в книге «Алгебра логики». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.
Л.Эйлер автор книг по математике, механике, движению планет, географии, кораблестроению, теории музыки. Школьники во всём мире решают задачи Эйлера, изучают теоремы, формулы, уравнения, ряды, методы решения задач Эйлера.
Умер Леонард Эйлер 18 сентября 1783 года от апоплексического удара. Похоронен на Смоленском лютеранском кладбище города Петербурга.
Название документа Пояснительная записка.docx
Урок разработан для класса численностью 5 человек, из которых
2 ученика относятся к одаренным детям; 1 - входит в группу риска.
В ходе урока рассмотрено решение задач разных типов (цветы, дом.животные, иност.языки, столовую, телефоны, читат.интересы, одноклассников, театры), чтобы у обучающихся была возможность убедиться в области применения кругов Эйлера имеет большое значение в нашей жизни; для сильных учеников подобраны олимпиадные задачи . На уроке учащиеся услышат истор. справку об ученом; повторят единицы длины, площади, объема и веса, как используемые в наши дни, так и старинные русские.
Накануне урока в уголок «Сегодня на уроке» повесить биографию Леонарда Эйлера; перечень задач, решаемых с помощью кругов Эйлера.
После урока предложить обучающимся написать сообщения по теме урока; подобрать или придумать задачи, решаемые кругами Эйлера.

| Автор | |
|---|---|
| Дата добавления | 15.03.2020 |
| Раздел | Математика |
| Подраздел | Конспект урока |
| Просмотров | 3207 |
| Номер материала | 6589 |