
Урок "Алгоритм решения квадратных уравнений"

Краткое описание документа:
Решение любой математической задачи предполагает знание точного предписания, определяющего, как от исходных данных перейти к искомому результату. Такое предписание называется алгоритмом решения.
В этом видеоуроке рассмотрен алгоритм решения квадратного уравнения
ax2 + bx + c = 0.
1. Поскольку число корней квадратного уравнения, а значит его решений, зависит от дискриминанта, то сначала целесообразно определить этот дискриминант. Возможно, что уравнение и вовсе не придется решать.
Итак, вычисляем дискриминант D по формуле D = b2 – 4ac. Далее следуем пунктам.
2. Если D<0, то квадратное уравнение ax2 + bx + c = 0 не имеет корней.
3. Если D=0, то квадратное уравнение имеет один корень, который находится по формуле
X = - (b/2a).
4. Если D>0, то квадратное уравнение имеет два корня, которые определяются по формулам x1 = ( (- b + √D) / (2a)), x2 = ( (- b - √D) / (2a)).
Этот алгоритм универсален, потому что с его помощью можно решать уравнения полные, и так называемые неполные квадратные уравнения. Полное квадратное уравнение – это уравнение ax2 + bx + c = 0, где b не равно 0 и с не равно 0.
Если в уравнении b=0 или с=0, то квадратное уравнение ax2 + bx + c = 0 называется неполным.
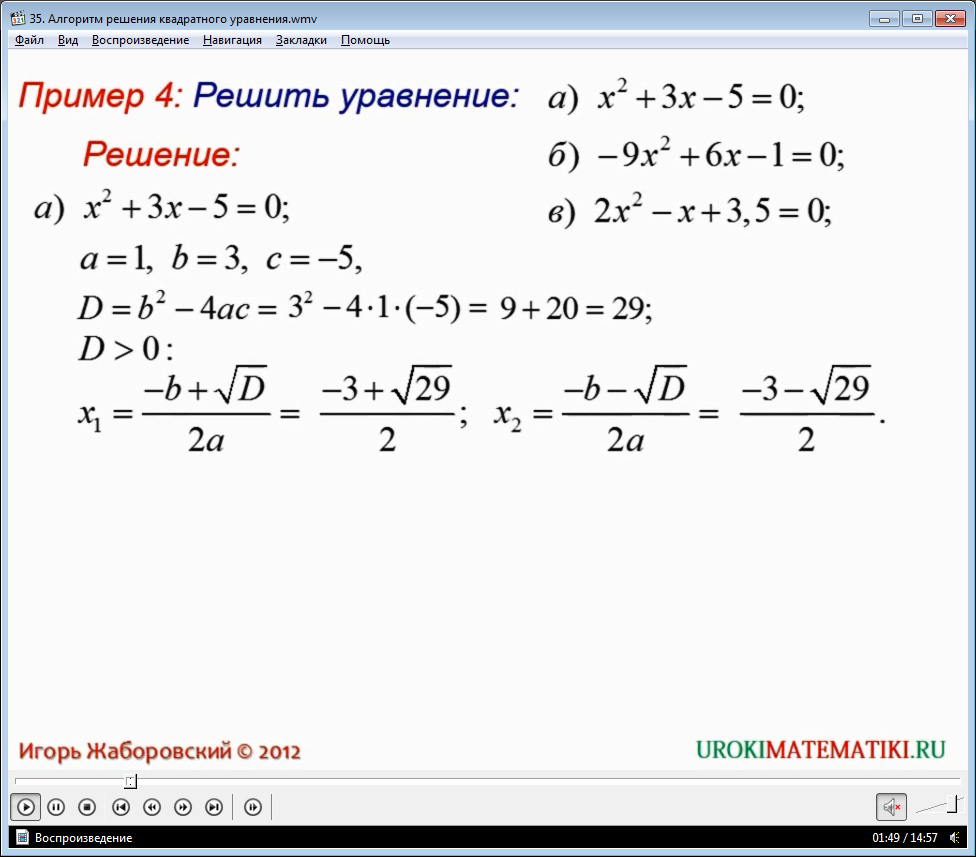
Рассмотрим решение некоторых уравнений. Например, x2 + 3x – 5 = 0. В видеоуроке показано, как применяется алгоритм решения. Дискриминант данного уравнения D=29, то есть D>0, значит, уравнение имеет два корня, которые мы и находим по формулам
x1 = (- b + √D) / (2a), x2 = (- b - √D) / (2a). В результате получаем ответ x1 = (- 3 + √29)/2 , x2 = (- 3 - √29)/2.
Некоторые уравнения нужно сначала преобразовать, а затем решать. Примеры решения таких уравнений показаны в видеоуроке.
Рассмотрим уравнение -9x2 + 6x – 1 = 0. Умножая обе части этого уравнения на -1, получим 9x2 – 6x + 1 = 0. Дискриминант данного уравнения D=0. Значит, согласно алгоритму, квадратное уравнение имеет один корень, который находится по формуле
X = - (b/2a). Этот корень x = 1/3.
Данное уравнение можно решить иначе. Как? Смотрите видеоурок.
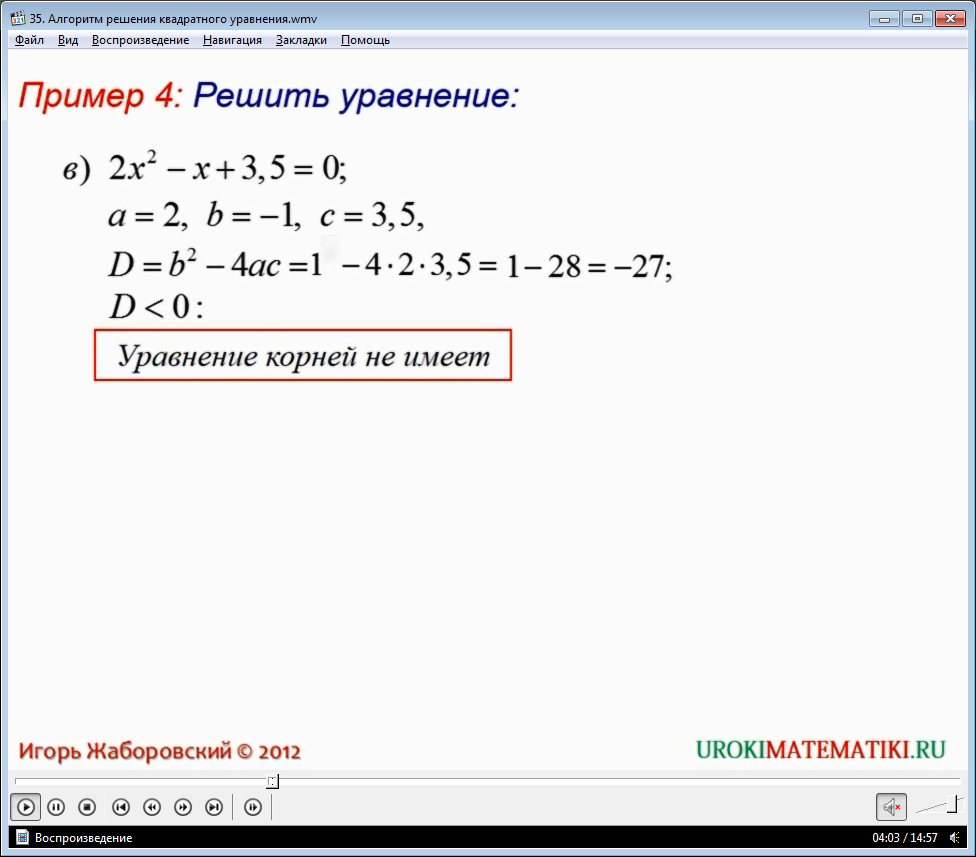
Следующее уравнение 2x2 – x + 3,5 = 0. Определяем дискриминант этого уравнения. Оказывается, что D= -27, то есть D<0, а это значит, что данное квадратное уравнение не имеет корней.
При решении уравнений для простоты записи можно сразу применить общую формулу корней x1,2 = (-b +- √D)/2a. Если окажется, что D = b2 – 4ac < 0, то корней нет.
Если D = b2 – 4ac = 0, то x1,2 = ( -b +- √0)/2a = -(b/2a) . Говорят, также, что уравнение имеет два равных корня, или корень кратности два.
Если же D = b2 – 4ac > 0, то уравнение имеет два корня, которые вычисляют по формулам x1 = (- b + √D) / (2a), x2 = (- b - √D) / (2a). Таким образом, квадратное уравнение можно решать подробно, как это показано в видеоуроке, либо сразу записать общую формулу, и с ее помощью делать необходимые вычисления.
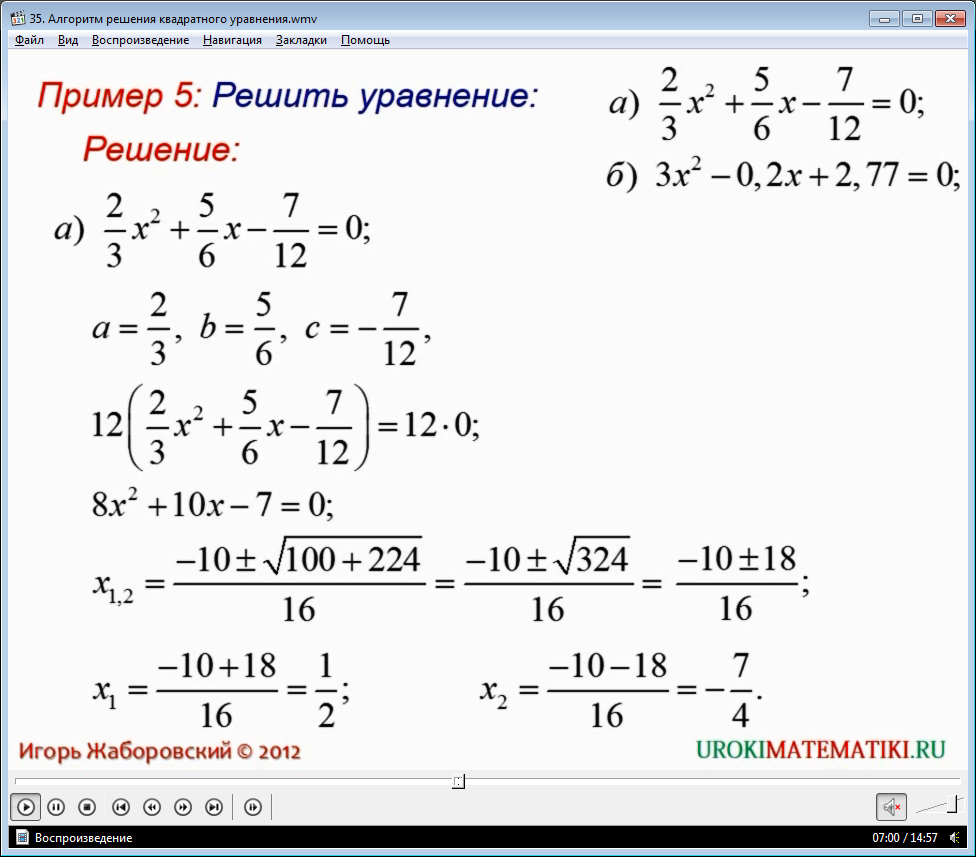
Рассмотрим пример 2/3x2 + 5/6x2 – 7/12 = 0. Мы видим, что коэффициенты и свободный член уравнения представляют собой дроби, с которыми неудобно работать. Как преобразовать и решить это и подобные уравнения, узнаем из видеоурока. Оттуда же поймем, когда удобнее пользоваться развернутым алгоритмом, а когда общей формулой.
Рассмотрим уравнение x2 – (2p + 1)x+ (p2 + p -2) = 0. Отличие этого уравнения состоит в том, что коэффициенты его являются буквенными выражениями. Говорят, что это уравнение с буквенными коэффициентами или с параметрами. Решение уравнений с параметрами требует особых навыков. В видеоуроке подробно и доступно показано решение таких уравнений и учет значений параметра при этом.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 12958 |
| Номер материала | 559 |