
Урок "Формулы корней квадратных уравнений"

Краткое описание документа:
Алгебраическое уравнение вида ax2 + bx + c = 0, где а не равно 0 называется квадратным уравнением с одной неизвестной.
Здесь а – коэффициент при х2, или первый коэффициент;
B – коэффициент при x (второй коэффициент), а c – свободный член.
На этом уроке мы рассмотрим, как находить корни такого уравнения.
Для нахождения корней нужно получить формулу. В видеоуроке подробно показано, как это сделать.
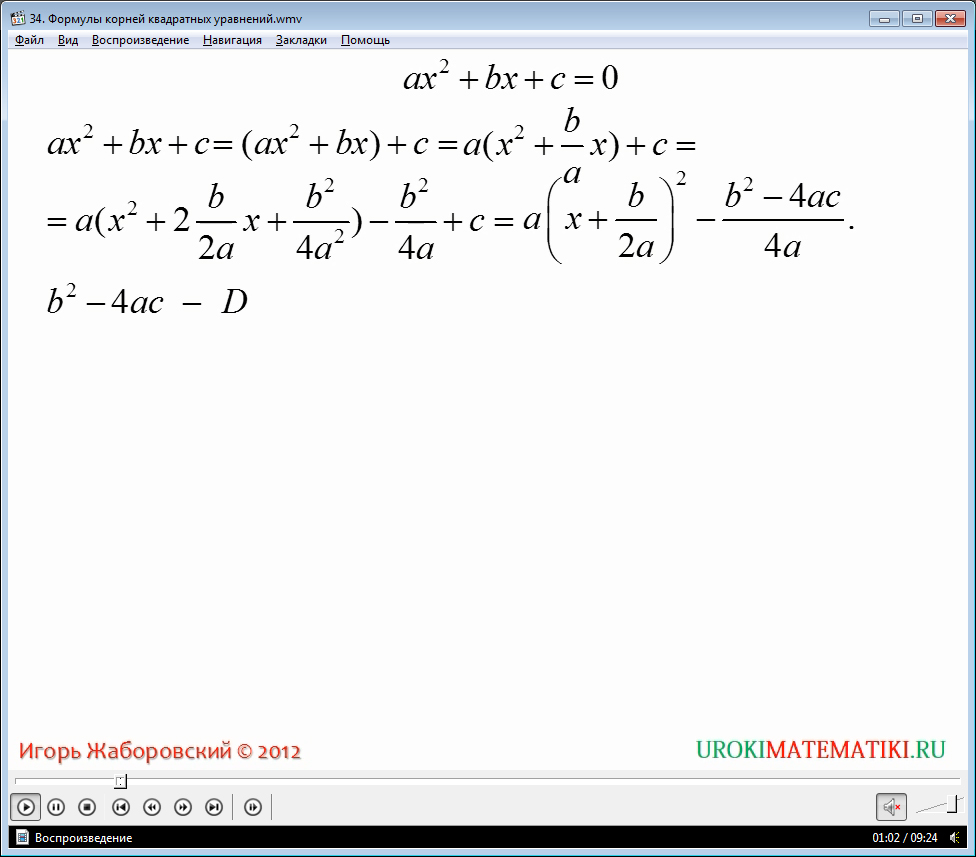
Итак, задано квадратное уравнение ax2 + bx + c = 0. Выделим полный квадрат двучлена из квадратного трехчлена. Это те преобразования, которые мы провели, чтобы доказать, что графиком функции y = ax2 + bx + c является парабола. Смотрим видеоурок и следим за преобразованиями.
У нас получается ax2 + bx + c = a(x + b/2a)2 – (b2 – 4ac)/4ac.
Выражение b2 – 4ac обозначают буквой D и называют дискриминантом квадратного трехчлена или дискриминантом квадратного уравнения ax2 + bx + c = 0.
Далее в видеоуроке показано, как наше квадратное уравнение можно привести к выражению (x + b/2a)2 = D/4a2. Такой вид записи удобен для определения числа коней уравнения и нахождения этих корней. Как это сделать? Смотрим видеоурок.
Теорема 1. Если D < 0, то квадратное уравнение ax2 + bx + c = 0 не приемлет корней. Доказательство теоремы показано в видеоуроке.
Например, возьмем уравнение 3x2 + 5x + 9 = 0. Дискриминант этого уравнения D = -83 меньше нуля. Значит, по теореме 1, наше уравнение не приемлет корней.
Аналогичный пример более подробно рассмотрен в видеоуроке.
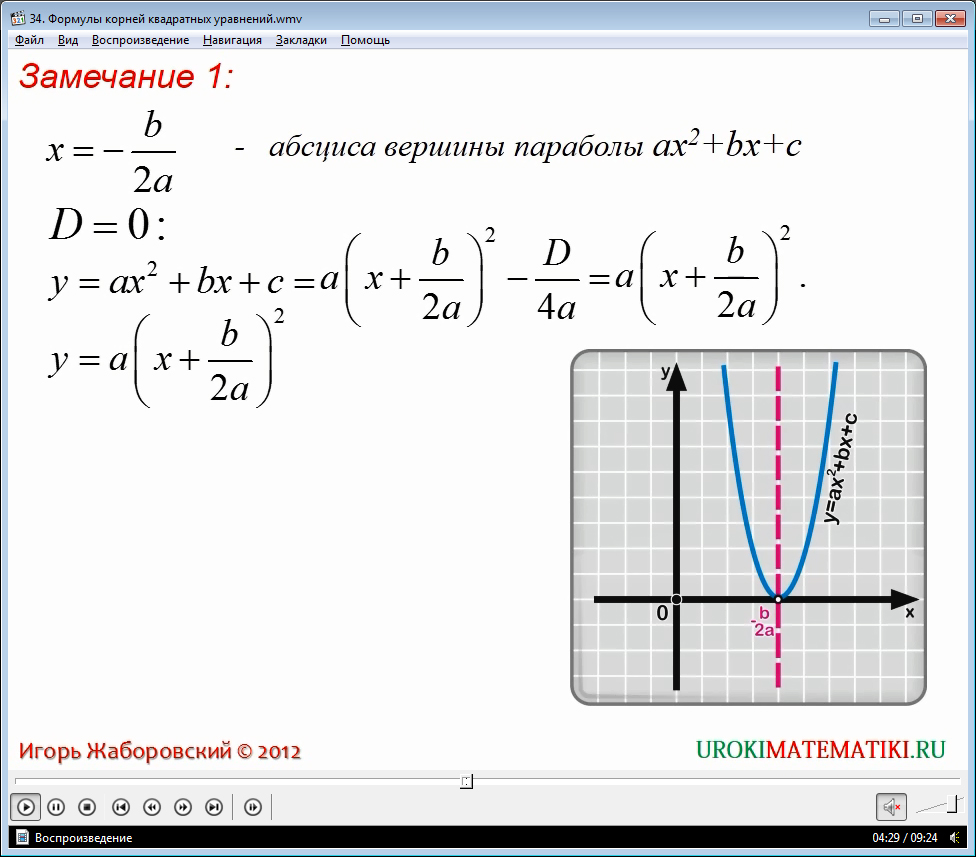
Теорема 2. Если D = 0, то квадратное уравнение ax2 + bx + c = 0 имеет один корень, который находится по формуле x = - b/2a.
Доказательство этой теоремы также смотрим в видеоуроке.
Напомним, что точка x = -b/2a является абсциссой параболы – графика функции y = ax2 + bx + c. Эта же точка – единственное решение уравнения ax2 + bx + c = 0 при равенстве нулю его дискриминанта. Более подробное объяснение смотрим в видеоуроке.
Рассмотрим пример 9x2 + 6x + 1 = 0. Дискриминант этого уравнения равен нулю, значит, это уравнение имеет один корень. По формуле x = -b/2a находим х = -1/3.
Пример можно решить и другим способом, если обратить внимание на то, что выражение 9х2 + 6х + 1 = (3х + 1)2 – полный квадрат. Аналогичный пример подробно разобран в видеоуроке.

Теорема 3. Если D > 0, то квадратное уравнение ax2 + bx + c = 0 имеет два корня, которые определяются по формулам x1 = (-b + √D)/2a, x2 = (-b - √D)/2a. Доказательство этой теоремы приведено в видеоуроке.
Рассмотрим пример 2x2 – 3x + 1 = 0. Найдем дискриминант уравнения, он окажется D = 1, то есть D > 0, и значит, это уравнение имеет два корня. По формулам теоремы 3 находим x1 = 1/2, x2 = 1. Решение аналогичного примера показано в видеоуроке.
Таким образом, число корней квадратного уравнения, а значит его решение, зависит от дискриминанта. Дискриминант различает уравнения по числу корней.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5053 |
| Номер материала | 558 |