
Урок "Графическое решение квадратных уравнений"

Краткое описание документа:
В 8 классе ученики столкнуться с рядом интересных тем по алгебре. Достаточно один раз хорошо понять, чтобы научиться использовать те или иные знания на практике. Эти знания пригодятся и в последующих классах при изучении, как алгебры, так и геометрии.
Некоторые темы, которые будут рассматриваться во время уроков алгебры в 8 классе, составят основу для новых разделов. Очень важно не пропускать уроки, а в случае пропусков, необходимо просмотреть самостоятельно материал, либо вместе с учителем. Важно это понимать. При самостоятельном либо индивидуальном изучении вам помогут мультимедийные презентации, уроки, иллюстрации. Все эти электронные ресурсы помогут ученикам быстрее и эффективнее усваивать тот или иной материал.
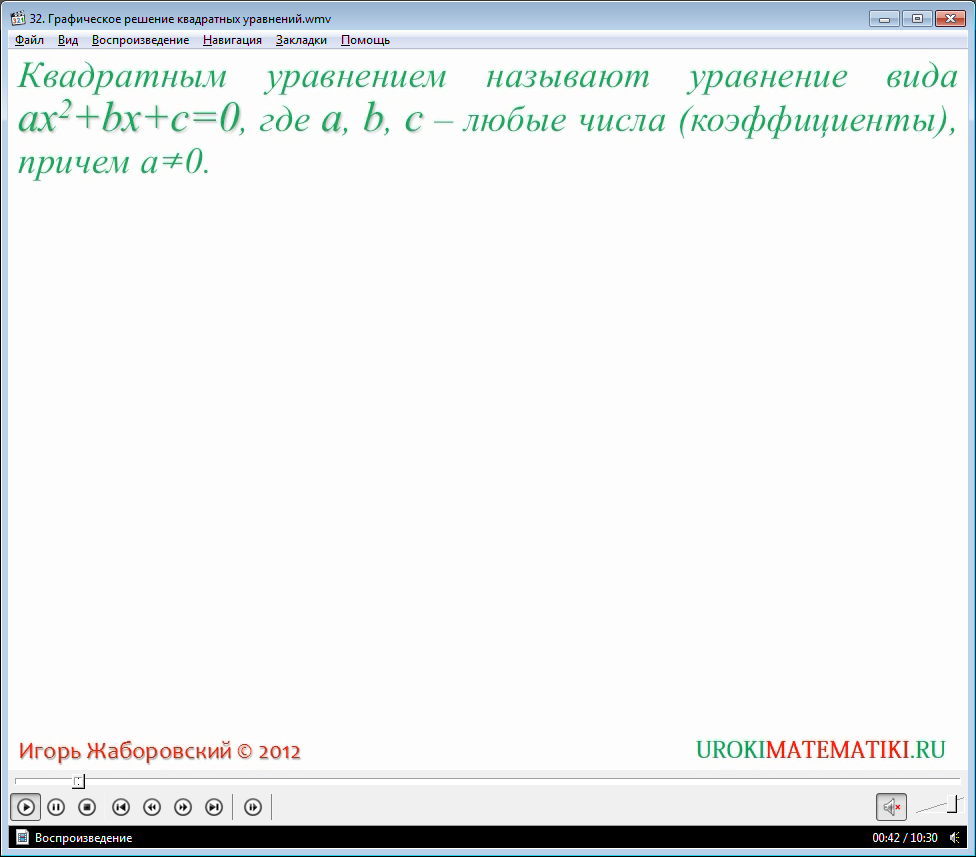
Одной из основных и важных тем из курса 8 класса алгебры является графическое решение квадратных уравнений. О том, что такое квадратное уравнение, школьники должны ознакомиться.
Данный видеоурок посвящен рассмотрению именно данной темы. Здесь будет рассказываться о том, как выглядят квадратные уравнения и каким образом можно с ними справиться.
Вначале видеоурока диктор объясняет, каким образом можно записать квадратное уравнение в общем виде. Мы видим три коэффициента, которые стоят перед неизвестным в квадрате, неизвестным в первой степени и свободный коэффициент.
Важно понимать, что коэффициент а перед неизвестным в квадрате не может равняться нулю. В противном случае, уравнение утратит свой смысл.
В качестве коэффициентов могут быть абсолютно любые числа. В зависимости от того, какими они являются,можно определиться, какой метод подойдет наиболее точно для решения того или иного примера.
Приводится пример решения простого квадратно уравнения, с целыми коэффициентами. Метод, как можно заметить, является графическим. Плюс такого метода заключается в наглядности и простоте.
Графиком функции квадратного уравнения будет являться парабола. Для ее построения необходимо знать ряд простых формул. Например, известна формула нахождения вершины параболы, зная коэффициенты а и b. Точки пересечения параболы с осью ох будут и являться решениями уравнения. Это очень просто можно обнаружить на графике.
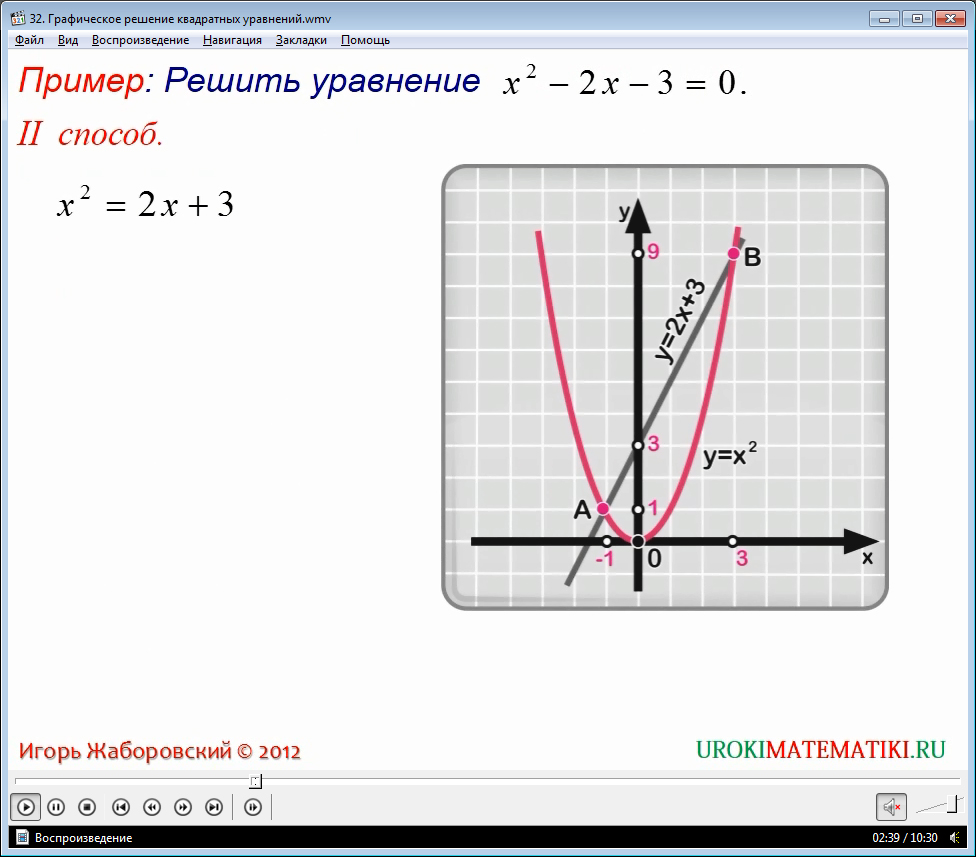
Есть также еще один графический метод решения квадратных уравнений. Диктор подробным образом объясняет также этот метод на примере несложного квадратного уравнения.
Суть заключается в том, что неизвестное х в квадрате переносится в левую часть уравнения. Таким образом, получаем две несложные функции, графики которых построить не составит никакого труда.
В правой части уравнения легко можно понять, что находится функция, графиком которой будет являться прямая. Построить прямую можно с помощью определения двух любых точек. А графиком функции, которая стоит с левой стороны, является парабола. Простую параболу построить восьмиклассники смогут без особых затруднений. Точками пересечений этих графиков будут являться корни, то есть, решения, уравнений.
На системе координат мы видим выполненные все обозначения. Выводится ответ. Диктор подробно комментирует каждый шаг. Школьники могут и при самостоятельном просмотре все понять.
На этом способе список не заканчивается. Существует еще один метод графического решения квадратного уравнения. Он является аналогичным с предыдущим. Необходимо перенести вместе с коэффициентом неизвестное в квадрате и свободный коэффициент. Получаем равенство, с двух сторон которого имеем две функции. При построении их графиков на координатной прямой, получим две точки пересечения. Таким образом, находится ответ.
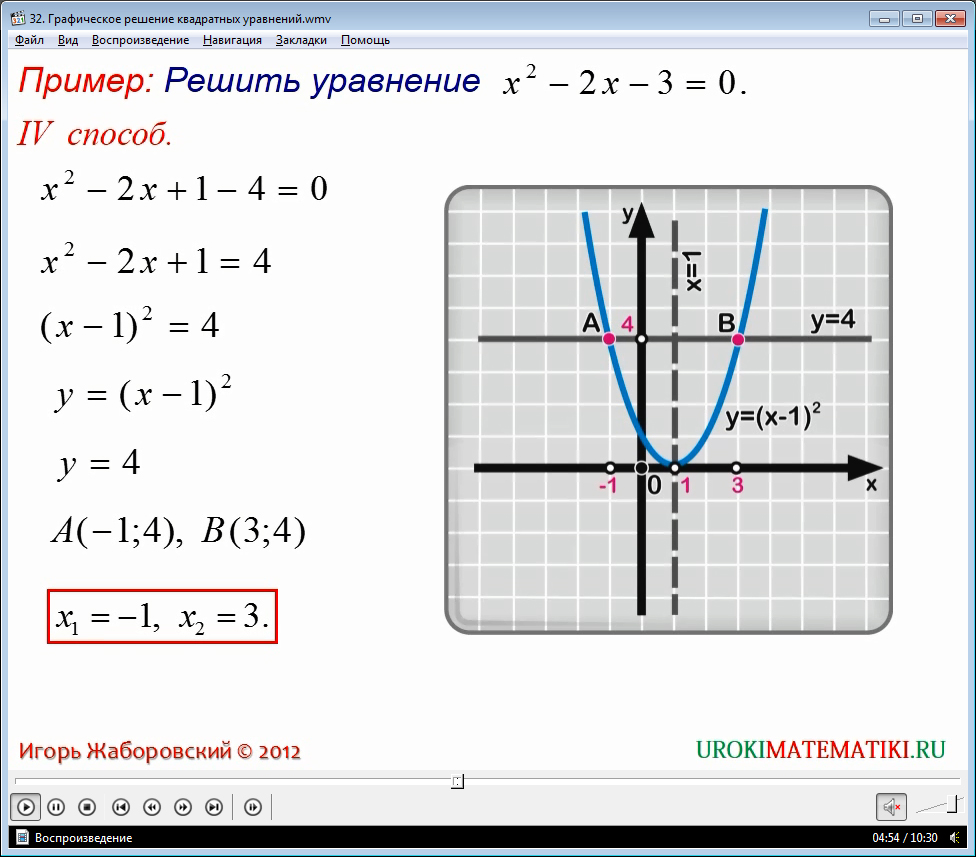
Четвертый способ графического решения квадратного уравнения заключается в том, чтобы привести данное уравнения в такой вид, с помощью которого можно будет увидеть некоторую формулу квадрата разности или суммы.
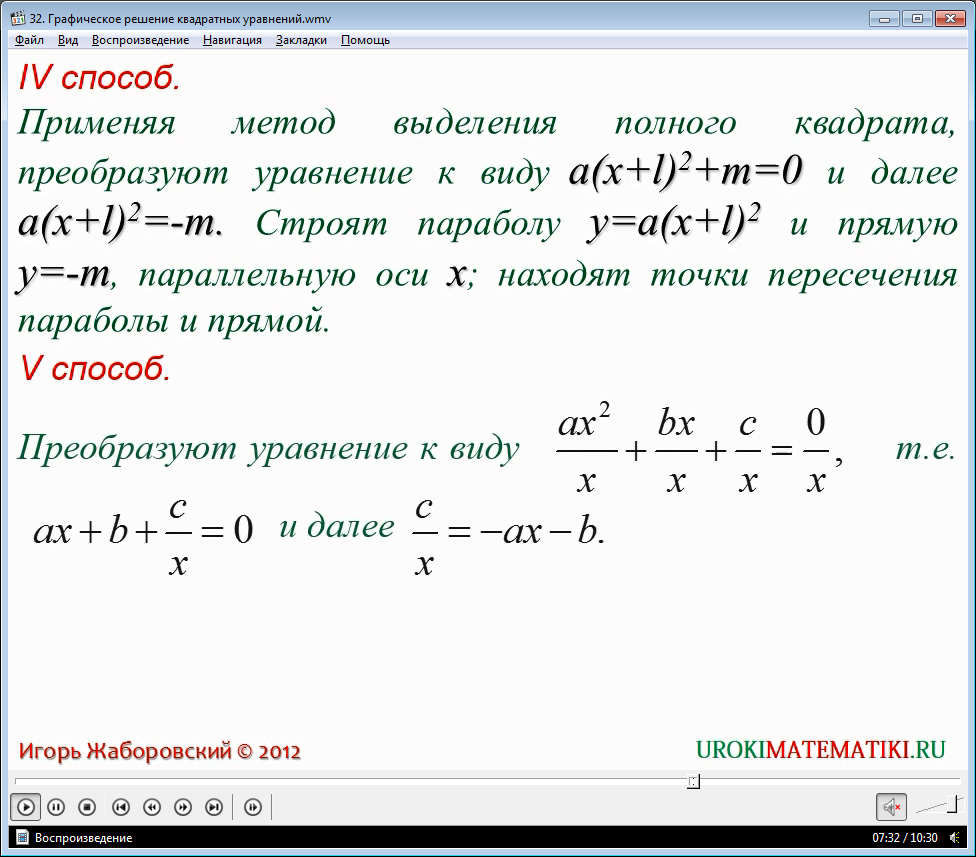
Эти формулы были ранее изучены. Стоит их вспомнить и уметь ими пользоваться. Перенеся оставшийся свободный коэффициент в другую сторону, опять же, получится парабола и прямая. Точки их пересечений и будут представлять собой решения.
Пятый способ, который рассматривается в видеоуроке, заключается в том, что каждый член многочлена делится на х. Таким образом появится дробь, в знаменателе которой стоит неизвестная. Перенеся ее в правую часть, получим функцию прямой с левой стороны и дробь – с правой. Далее необходимо построить их графики, после чего – найти точки пересечения.
Следующая часть презентации посвящена теоретическому обобщению всех методов. Для того, чтобы научиться с ними справляться, необходимо закрепить изученный материал на практике.
При обобщении этих методов, можно обновить в памяти рассмотренный материал.
Последняя часть видеоурока посвящена замечаниям. Стоит помнить, что не всякое квадратное уравнение можно решить графическим методом. Если уравнение явно подходит под тот или иной метод, стоит подумать. Однако, если уравнение отличается от рассмотренных примеров, не стоит зацикливаться на этом.
На этом можно закончить урок. Он является последовательным и имеет четкую структуру.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6001 |
| Номер материала | 555 |