
Урок "Деление с остатком"

Краткое описание документа:
Видеоурок «Деление с остатком» наглядно представляет учебный материал, необходимый для освоения пятиклассниками данной темы. В ходе данного видеоурока рассматривается особенность деления, в результате которого не образуется натуральное число, так как нацело делимое на делитель не делится, особенности операции деления с остатком, а также правила нахождения частного от деления с остатком, обратных операций - нахождения неизвестного делимого и делителя, зная, что полученное частное – с остатком. Используя видеоурок, учитель может быстрее достичь целей обучения, повысить эффективность занятия. Это достигается благодаря приемам, которые применяются в ходе составления видео.
В данном видео используются иллюстрации, анимационные эффекты, выделение текста цветом и типом шрифта, озвучивание. Все эти приемы дают возможность оказывать дополнительное воздействие на мыслительные процессы ученика, способствуя лучшему пониманию и запоминанию материала.
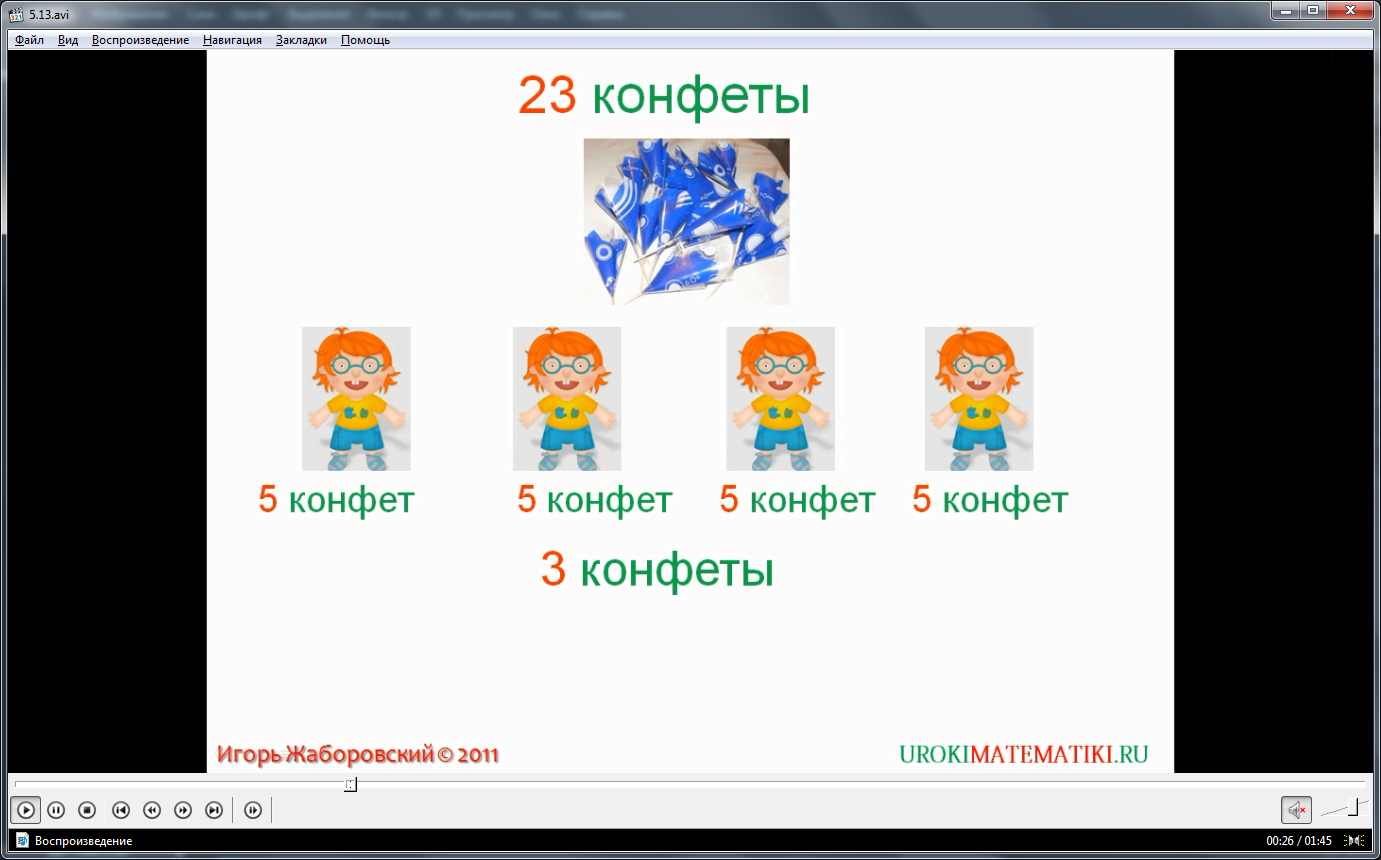
Видеоурок начинается с представления темы урока. Отмечается, что деление нацело натуральных чисел не всегда возможно. В качестве примера дается иллюстрированная математическая задача. На экране изображается некоторое количество конфет, к картинке есть указание их числа – 23 конфеты. Ниже изображены 4 ребенка. Предлагается практическая задача – бабушке необходимо разделить имеющиеся у нее конфеты поровну между внуками.

Отмечается, что при решении данного задания можно поровну дать внукам только по 5 конфет, но при этом останется 3 конфеты, которые не делятся на 5 внуков. Данная операция представлена делением чисел с остатком. Далее эта операция рассматривается более подробно. Деление с остатком производится в столбик. При делении 23:4 число, которое дает возможность раздать максимальное количество конфет – 5. При его умножении на 4 ,получается 20. Однако после вычитания 20 из 23 получается остаток 3, который не делится на 4. Ниже отмечается, что остаток всегда является меньше, чем делитель. То есть 3<4. При этом члены выражения 23 – это делимое, а 4 – делитель, при этом 5 – неполное частное. Название членов выражения выделены с помощью указателей.
Далее рассматриваются особенности остатка. Отмечается правило, что если остаток равен нулю, то считается, делимое нацело можно разделить на делитель, без остатка. Правило выделено цветом для запоминания.
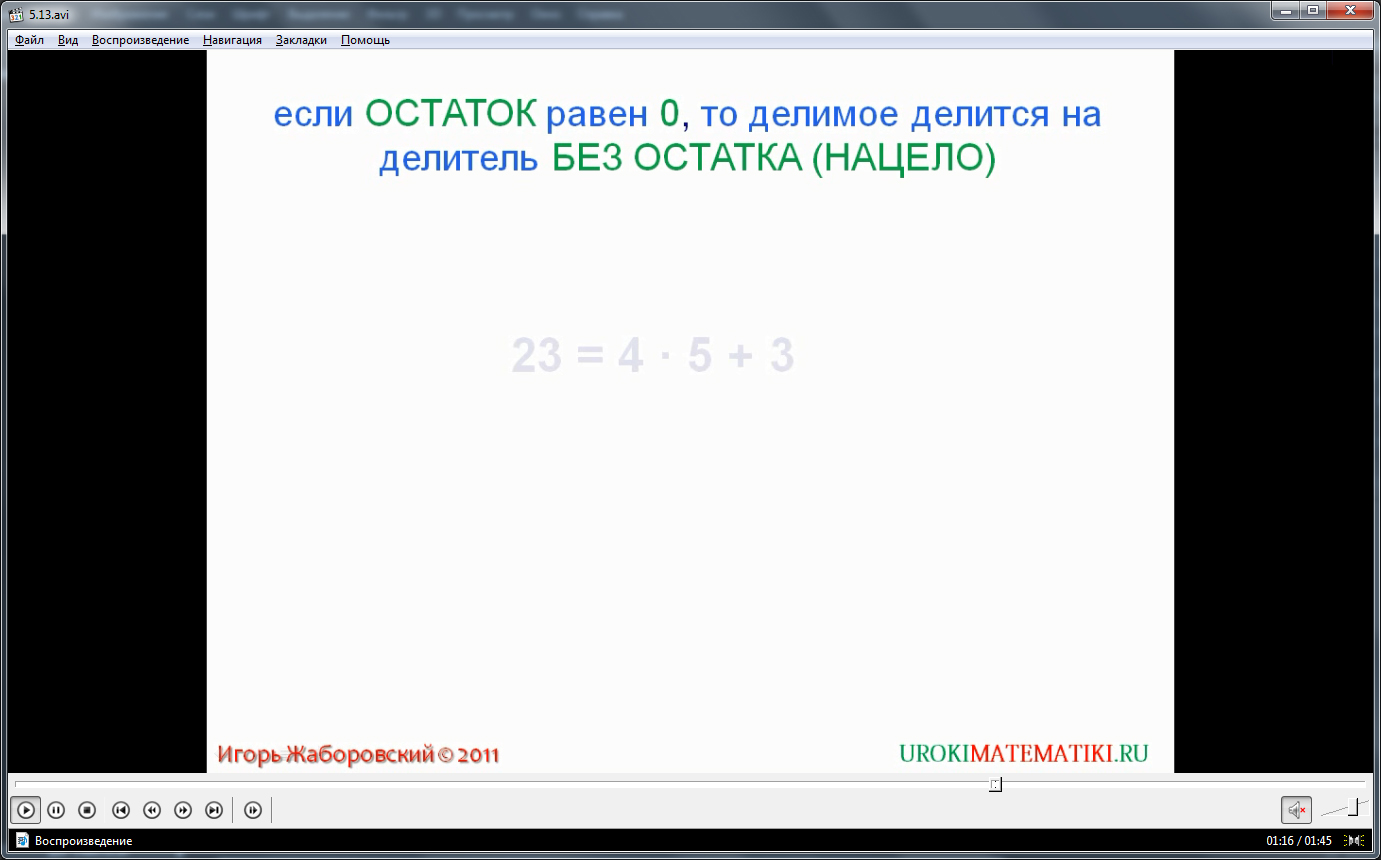
Число 23 нельзя представить как произведение, однако его можно представить как сумму произведения и остатка, то есть 23=4·5+3. Правило поиска делимого по данному делителю, остатку, частному представлено ниже в текстовом виде. Описано, что для вычисления делимого, выполняя деление с остатком, требуется делитель перемножить с неполным частным, к произведению добавить остаток. Правило выделено цветом, рекомендовано к запоминанию.
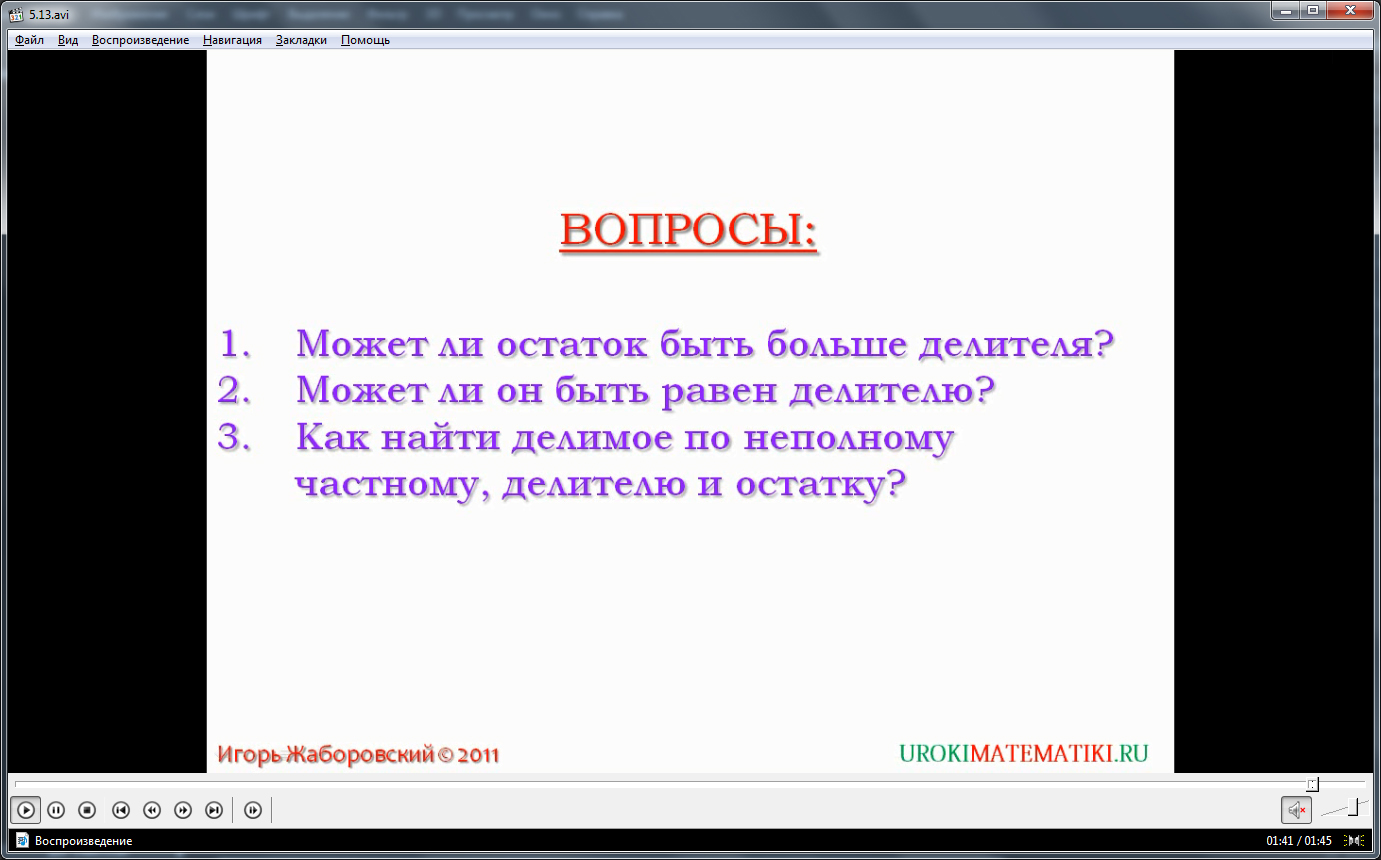
В конце видеоурока ученикам рекомендуется ответить на вопросы для проверки усвоения материала. Представлено 3 вопроса. В первом спрашивается, может ли остаток деления быть больше, чем делитель, во втором – допускается ли равенство остатка и делителя, в третьем - как отыскать делимое по известным делителю, неполному частному, получившемуся остатку.
Видеоурок «Деление с остатком» рекомендуется применять для повышения эффективности обычного школьного урока математики. Также наглядный материал будет полезен учителю, который осуществляет дистанционное обучение. Видео поможет освоить учебный материал ученику, самостоятельно изучающему или повторяющему тему урока.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 5612 |
| Номер материала | 1103 |