
Урок «Движения. Осевая симметрия»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы продолжаем знакомство с движением.
На прошлом занятии вы познакомились с одним из видов движения — центральной симметрией.
Вспомним, что центральная симметрия — это такое отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К1, относительно центра симметрии точки В.
Отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К1 относительно оси а называется осевой симметрией с осью а.
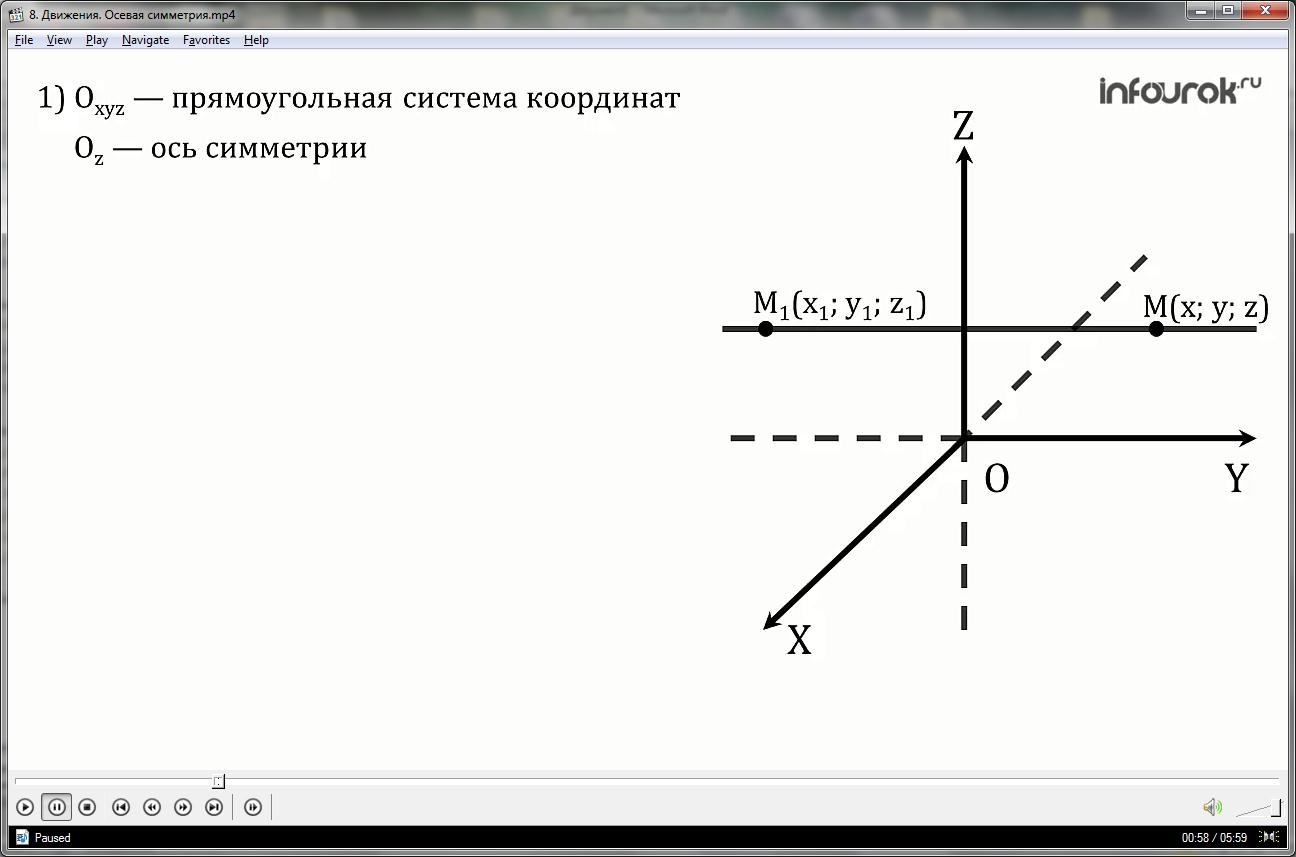
1. Введём декартову (прямоугольную) систему координат Оxyz так, чтобы ось Оz совпала с осью симметрии.
2.Найдем связь между точками М (x;y;z) и M1 (x1;y1;z1), которые симметричны относительно оси Оz .Если точка М не принадлежит оси Оz, то данная ось:
а) проходит через середину отрезка МM1;
б) перпендикулярна отрезку ММ1.
Из первого условия по формулам для координат середины отрезка имеем:
Откуда:
x=-x1 ; y=-y1
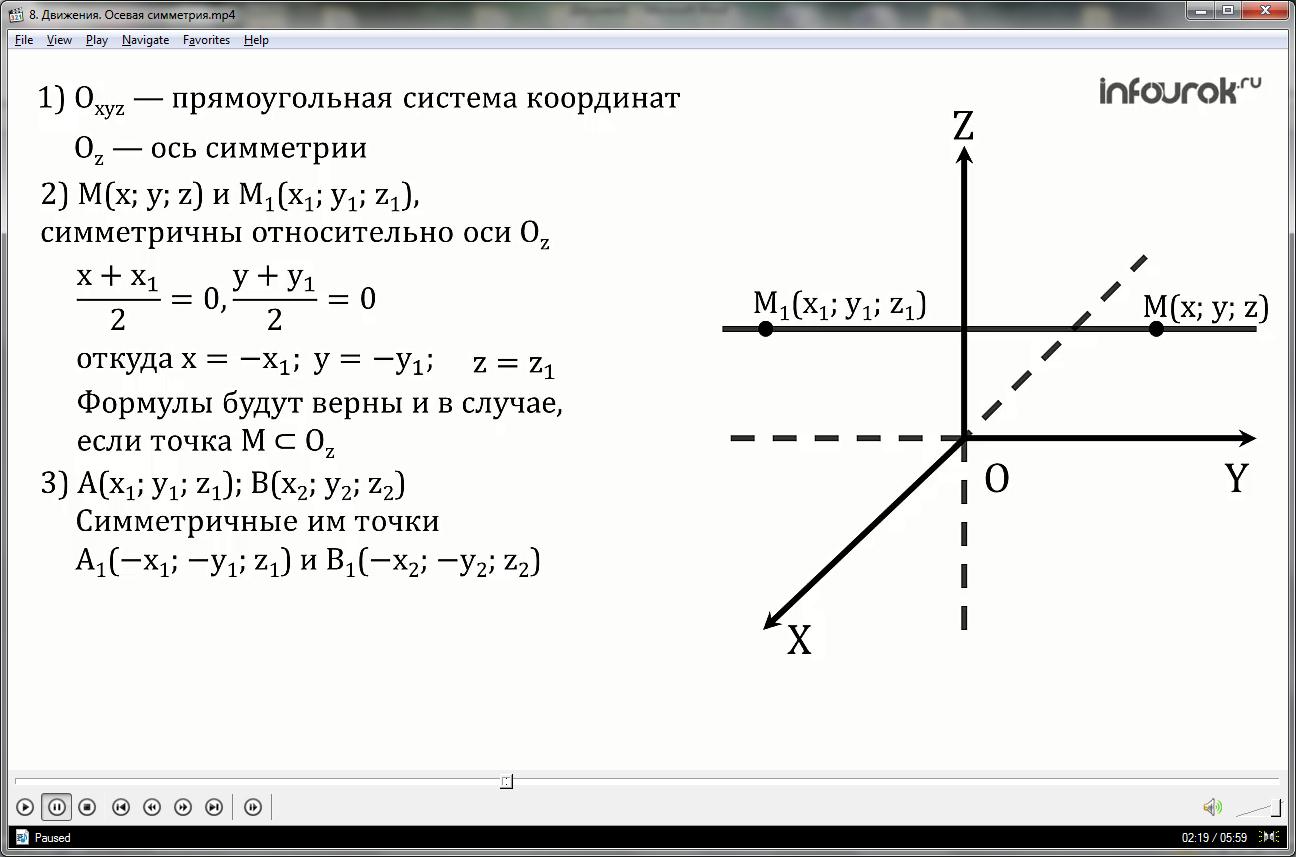
Из второго условия можно сделать вывод, о том, что z=z1.
Данные формулы будут верны и в случае, если точка М принадлежит оси Оz.
3. Рассмотрим любые две точки: А — с координатами (x1;y1;z1) и В — с координатами (x2;y2;z2) и докажем, что расстояние между точками А1 и В1, которые им симметричны, равно АВ.
Точки А1 и В1 имеют координаты
А1 (-x1;-y1;z1) и В1 (-x2;-y2;z2).
По формуле расстояний между двумя точками, найдём:
АВ=
A1B1=
Очевидно, что длина отрезка АВ равна длине отрезка A1B1, то есть расстояние между точками сохранено.
Таким образом, мы доказали, что осевая симметрия является движением.
Рассмотрим решение задач, применяя полученные знания.
Задача 1.
Доказать, что при осевой симметрии прямая, образующая с осью симметрии угол , отображается на прямую, так же образующую с осью симметрии угол
Решение:
1. Так как ось симметрии а и прямая l не параллельны, то а пересекается с l в некоторой точке А.
Выберем любую точку N на прямой l.

Построим отрезок NE перпендикулярно к оси симметрии а.
Затем продолжим отрезок NE за точку Е на расстояние EF=NE.
Соединим точки F и А.
2. Рассмотрим прямоугольные треугольники AEF и AEN.
EF=NE (по построению), АЕ — общий катет.
Таким образом, прямоугольные треугольники AEF и AEN равны.
Из равенства данных треугольников следует равенство углов EAN и EAF, а это и есть угол .
Итак, мы доказали, что при осевой симметрии прямая, образующая с осью симметрии угол , отображается на прямую, также образующую с осью симметрии угол
Задача 2.
Известно, ABCDA1B1C1D1 — куб, длина ребра АВ равна а. Точка D отображается в точку D2 при осевой симметрии относительно прямой В1 D1. Найти ВD2.

Решение:
1.Отрезок DD1 перпендикулярен плоскости A1C1D1 верхнего основания куба.
По определению осевой симметрии отрезки DD1 и D1D2 равны. Значит DD2=2а
2.Из прямоугольного треугольника ABD найдём гипотенузу BD по теореме Пифагора:
BD=√АВ2+AD2=√а2+а2=а√2
3.Так как треугольник BDD2 так же прямоугольный, то по теореме Пифагора найдем длину искомого отрезка ВD2:
ВD2=√ DD22+ BD2=
√(2а)2+( а√2)2=√4а2+2а2=а√6
Таким образом, длина отрезка ВD2 равна а√6.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 10342 |
| Номер материала | 994 |