
Урок «Движения. Параллельный перенос»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы продолжаем изучать движения.
На прошлом занятии вы познакомились ещё с одним видом движения — зеркальной симметрией.
Напомню, что зеркальной симметрией называется такое отображение пространства на себя, при котором каждая точка К переходит в симметричную ей относительно плоскости β точку К1.
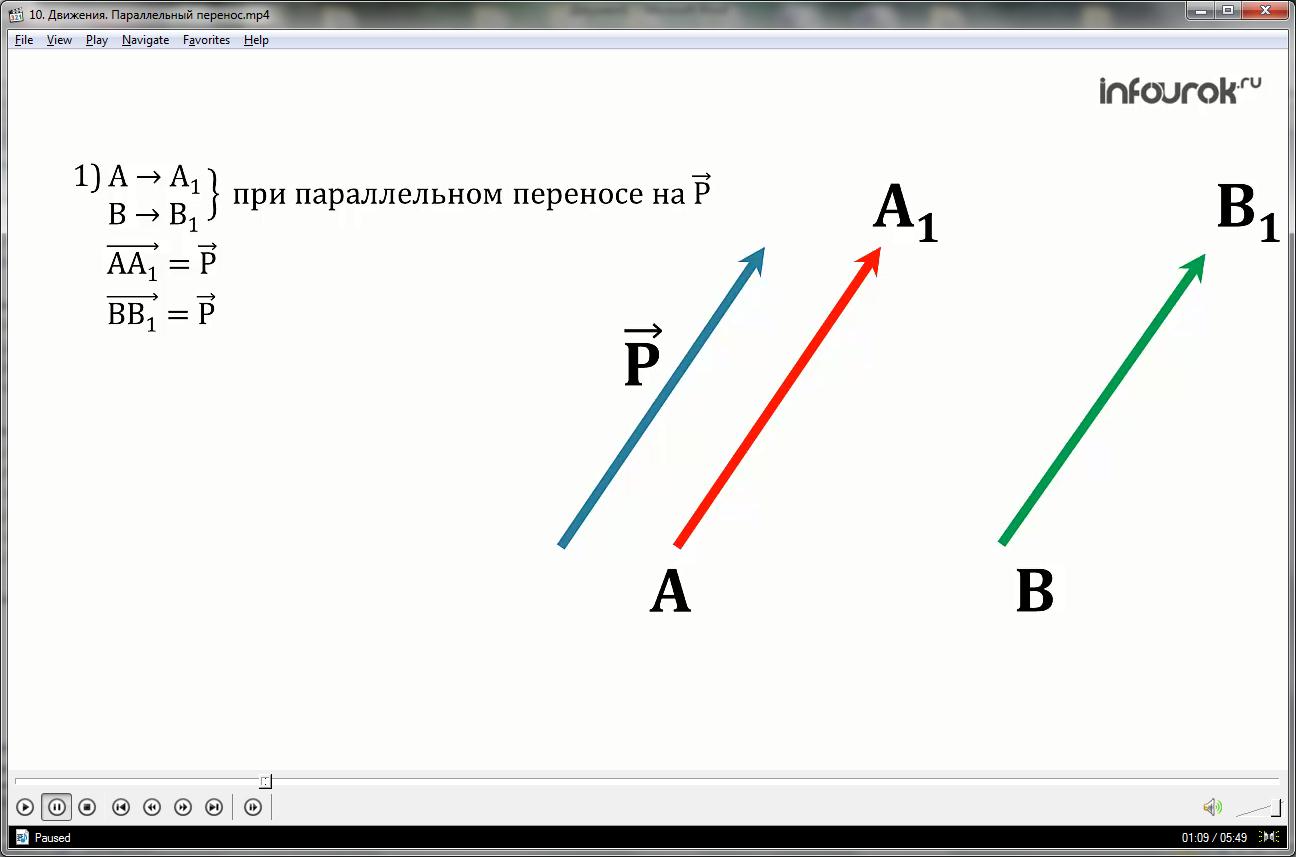
Отображение пространства на себя, при котором любая точка М переходит в такую точку М1, что вектор ММ1 равен вектору p –называется параллельным переносом на вектор p.
1. По определению параллельного переноса на вектор p, любые две точки А и В переходят в точки А1 и В1, так что вектор АА1 равен вектору p и вектор ВВ1 равен вектору p.
2.По правилу треугольника имеем:
АВ1=АА1+А1В1
Одновременно:
АВ1=АВ+ВВ1
3.Приравняем правые части полученных равенств:
1+ = + 1
Так как вектора АА1 и ВВ1 — это есть вектор p, получим:
+ 1= + , откуда
1= , таким образом, получили, что расстояние между точками А и А1, В и В1 сохранено, значит параллельный перенос на вектор p является движением.
В какую фигуру при движении отображается отрезок, прямая, плоскость? (Пауза)
При движении отрезок переходит в отрезок, прямая — в прямую, плоскость — в плоскость.

Любое наложение, с помощью которого доказывается равенство фигур, также является движением.
Применим полученные знания при решении задач.
Задача 1.
Треугольник А1В1С1 получен параллельным переносом треугольника АВС на вектор p. Точки М и М1 — соответственно точки пересечения медиан треугольников АВС и А1В1С1. Доказать, что при параллельном переносе на вектор p точка М переходит в точку М1.
Доказательство:
1.Движение — это отображение пространства на себя, сохраняющее расстояние между точками. Параллельный перенос является движением, значит АВ=А1В1, ВС=В1С1, АС=А1С1.
Треугольники АВС и А1В1С1 равны по третьему признаку равенства треугольников.
2.Дополнительное построение: проведём отрезки АМ и А1М1. Они также будут равными (проведены в равных треугольниках).
3. Для плоского четырёхугольника АММ1А1 имеем: АМ║ А1М1 и АМ = А1М1
4.Таким образом, по признаку параллелограмма, АММ1А1 — параллелограмм, откуда вектор АА1 равен вектору ММ1 равен вектору p.

Мы доказали, что при параллельном переносе на вектор p точка М переходит в точку М1.
Что и требовалось доказать.
Задача 2.
В каком месте следует построить мост MN через реку, разделяющую две данные деревни А и В, чтобы путь АМNВ из деревни А в деревню В был кратчайшим? (берега реки считаются параллельными прямыми, мост строится перпендикулярно реке).
Решение
1.Предположим, что некоторое положение моста найдено.
При параллельном переносе, переводящем точку М в точку N, точка А перейдет в некоторую точку А1.

2. Тогда АМ+МN+NВ=АА1+А1N+NB АА1+А1В (для того чтобы три точки не лежали на одной прямой, должно выполняться неравенство треугольника — сумма двух сторон больше третьей), причем равенство достигается, когда точки А1, N, и В лежат на одной прямой.
3.Отсюда вытекает следующий способ построения: выполним параллельный перенос точки А на вектор . Точка А переходит в точку А1.
Соединив точку А1 с точкой В, получим точку Д, которая и будет точкой начала моста.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 13068 |
| Номер материала | 996 |