
Урок «Движения. Зеркальная симметрия»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы продолжаем знакомство с движением.
На прошлом занятии вы узнали об ещё одном виде движения — осевой симметрии.
Напомню, что осевая симметрия с осью а — это отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К1 относительно оси а.
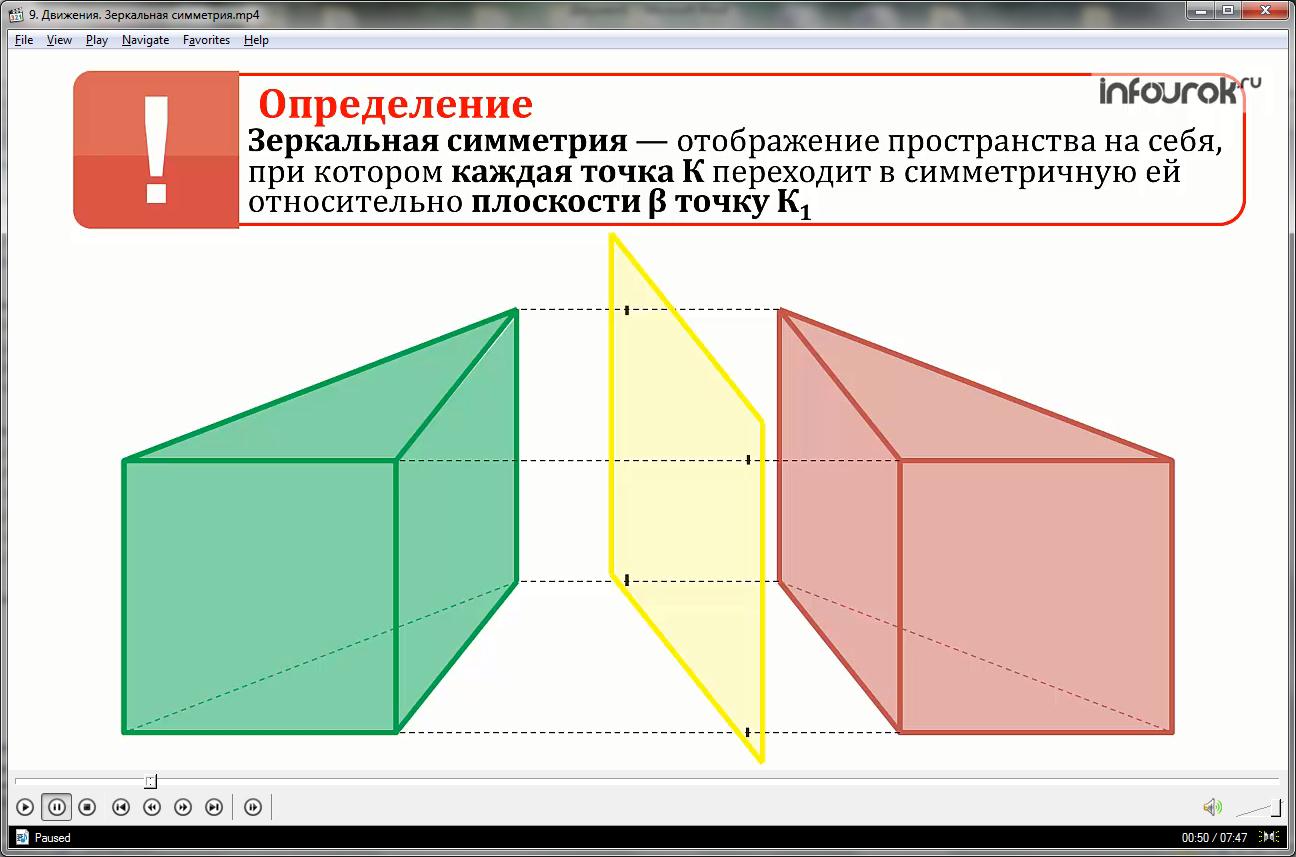
Отображение пространства на себя, при котором каждая точка К переходит в симметричную ей относительно плоскости β точку К1 называется зеркальной симметрией (симметрией относительно плоскости β).
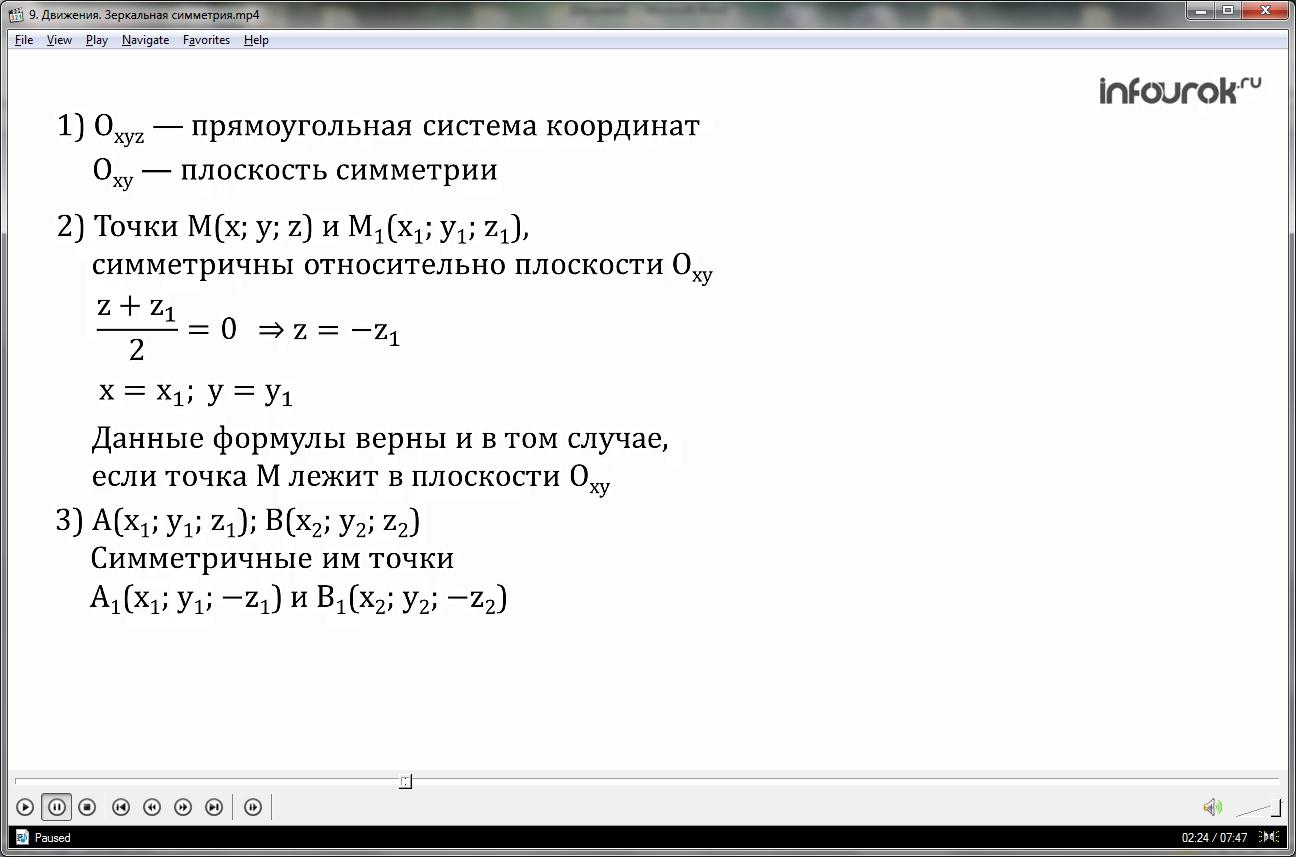
1. Введём декартову (прямоугольную) систему координат Оxyz так, чтобы плоскость Оxy совпала с плоскостью симметрии.
2. Найдем связь между точками М (x;y;z) и M1 (x1;y1;z1), которые симметричны относительно плоскости Оxy. Если точка М не принадлежит данной плоскости, то плоскость Оxy :
а) проходит через середину отрезка МM1;
б) перпендикулярна отрезку ММ1.
Из первого условия по формулам для координат середины отрезка имеем:
z+z1 =0, откуда z=-z1
Из второго условия следует, что отрезок МM1 параллелен оси аппликат Оz , таким образом, x=x1; y =y1.
Данные формулы верны и в том случае, если точка М лежит в плоскости Оxy.
3. Рассмотрим любые две точки: А — с координатами (x1;y1;z1) и В — с координатами (x2;y2;z2) и докажем, что расстояние между точками А1 и В1, которые им симметричны, равно АВ.
Точки А1 и В1 имеют координаты
А1 (x1;y1;-z1) и В1 (x2;y2;-z2).
По формуле расстояний между двумя точками, найдём:
АВ=√(х2-х1)2+(y2-y1)2+(z2+z1)2
A1B1=√(-х2-х1)2+(-y2-y1)2+(-z2+z1)2,
Очевидно, что длина отрезка АВ равна длине отрезка A1B1, то есть расстояние между точками сохранено.
Таким образом, мы доказали, что зеркальная симметрия является движением.
Разберём несколько задач, применяя полученные знания.
Задача 1.
Доказать, что прямые а и а1 лежат в одной плоскости, если при зеркальной симметрии прямая а отображается в прямую а1.
Решение:
1. Введём плоскость симметрии Оxy.
Рассмотрим два случая:
- прямая а параллельна плоскости Оxy.
- прямая а не параллельна плоскости Оxy.
В случае параллельности прямой а и плоскости Оxy имеем: точки М и L, N и K симметричны (принадлежат симметричным прямым), тогда MA=AL, NB=BK.
Кроме того, все эти отрезки равны между собой: MA=AL=NB=BK, поскольку плоскость Оxy — плоскость симметрии.
Прямые МL, NK — перпендикулярны плоскости Оxy, значит МL параллельна NK (две прямые, перпендикулярные плоскости, параллельны между собой).
Таким образом, мы получили, что четырёхугольник MLKN — прямоугольник.
Поэтому прямые LK и MN параллельны как противоположные стороны прямоугольника MLKN. А значит, и прямые а и а1, на которых лежат параллельные прямые LK и MN, будут параллельными, а значит, и лежат в одной плоскости.
Что и требовалось доказать.

2.В случае, если прямая а не параллельна плоскости Оxy, прямая а пересекает данную плоскость в точке Р.
При симметрии точка Р переходит в себя, так как лежит в плоскости симметрии Оxy.
Таким образом, точка Р принадлежит и прямой а1.
Мы получили, что прямые а и а1 имеют общую точку, следовательно, они лежат в одной плоскости.
Что и требовалось доказать.
Итак, мы доказали, что прямые а и а1 всегда лежат в одной плоскости, если при зеркальной симметрии прямая а отображается в прямую а1.
Задача 2.
При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β1. Доказать, что если плоскость β параллельна плоскости α, то плоскость β1 также параллельна плоскости α.
Доказательство:
1.Выберем три точки А, В, С в плоскости β, не лежащие на одной прямой.
2.Дополнительное построение: проведём отрезки АА2, ВВ2, СС2 перпендикулярно плоскости α.
Продолжим эти отрезки за точки А1, В1, С1 так, что А2А1=АА2, В2В1=ВВ2, С2С1=СС2.
Мы получили, что четырёхугольник АА1В1В — прямоугольник, так как АА1=ВВ1 и АА1║ВВ1(в силу симметричности плоскостей β и β1).
3.Таким образом, А1В1║АВ, ВВ1=СС1 и ВВ1║СС1, значит ВВ1С1С — прямоугольник.
Поэтому В1С1║ВС.
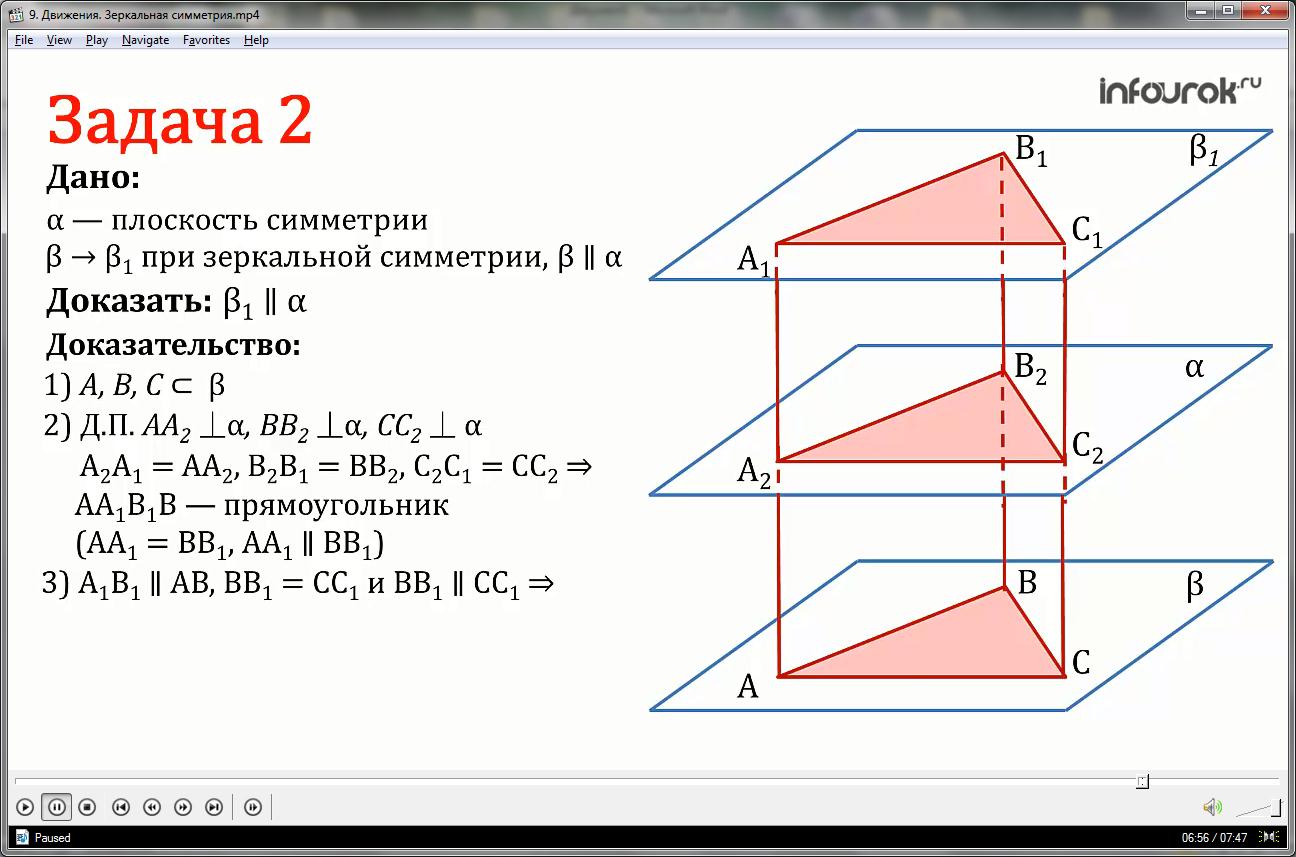
4.Плоскость β проходит через точки А1, В1, С1 и эта плоскость единственна.
5. Известно, что если пересекающиеся прямые (ВА и ВС) одной плоскости (β) параллельны двум пересекающимся прямым (В1А1 и В1С1) другой плоскости (β1), то эти плоскости параллельны.
Итак, мы доказали, что плоскости β и β1 параллельны.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 11822 |
| Номер материала | 995 |